10/15(火)-10/19(土)　岐阜県（南濃温泉「水晶の湯」）で自動運転車の実証実験を行います☆彡

16-7. ポケモンで分かる二項検定とZ検定の違い

はじめに

「一撃必殺技」は30%の確率で当たれば、どんなにステータスに差があってもひんしにさせることができます。

主な一撃必殺技

  • ハサミギロチン
  • つのドリル
  • じわれ
  • ぜったいれいど
ハサミギロチンを受けるカメ
ぜったいれいどを放つネッシー

手持ちの３匹がみんな一撃必殺技でやられてしまったら「確率バグってるのでは？」 と疑いたくなります。今日は二項検定とZ検定を学んで、本当にバグと言えるのかを調べてみます。

二項検定を調べてみたけど

とりあえず、「二項検定」で検索して上位に出現する以下のサイトは二項検定ではなくZ検定です。

25-2. 二項分布を用いた検定 - 統計WEB
25-1章の母比率の検定と同じ問題について、この章では二項分布を用いた検定を行ってみます。 例題： あるサイコロを12,000回投げたときに1が2,200回出ました。このサイコロはどの目も等しく出る歪みのないサイコロとい … 続きを読む 25-2. 二項分布を用いた検定
bellcurve.jp

本文中に「二項検定」という単語が入っていないのになんで検索に引っかかるのでしょうか。二項検定とZ検定は別物ですので、二項検定の説明に「Z」は登場しないと考えてください。

検定とは

統計学では、まず「～には差がある」という仮説を立てることから始めます。

例えば、

  • マクドナルドよりもケンタッキーのポテトの方が本数が多い
  • A型インフルエンザとB型インフルエンザの致死率には差がある

のような仮説を立てます。これらの証明したい仮説のことを「対立仮説」と呼びます。これらの反対の「差はない」とする仮説のことを「帰無仮説」と呼びます。対立仮説と帰無仮説のどっちが正しいの？というのを調べるのが統計学での検定です。

「差がある」ことを主張するためには、「差がない」とする帰無仮説を棄却する作業を行います。帰無仮説を棄却するというのは、「差がないにしてはおかしいことが起きていますよね？だから差はあります」ということです。

帰無仮説が棄却されれば「差がある」ことが主張でき、帰無仮説が棄却されなければ「差があるかないかわからない」ということになります。帰無仮説が棄却されなかったからといって「差がない」とは言えないことに注意です。（ここテストに出ます。Natureでも指摘されています。）

※「差がない」ことを主張した例を見たことがないので、事例を教えてください。

二項検定とは

二項検定は「二項分布を用いた統計的仮説検定」です。

ベルヌーイ試行

「技が当たるか当たらないか」 のように結果が２つしかない試行のことを「ベルヌーイ試行」といいます。なんでもないことでもカタカナにするとカッコいいですね。

ベルヌーイ試行では、一般に２つの結果のうち一方を「成功」とし、確率変数Xがとる値を「１」。もう一方を「失敗」とし、Xがとる値を「０」とします。要は起こったら嬉しい方を１、悲しい方を０にしようということです。

成功した時の確率をpとして式で表すと、成功時は

    $$ P[X=1]=p $$

失敗時は

    $$ P[X=0]=1-p $$

と表せます。

一撃必殺技は当たる場合が成功の方で、当たる確率が30%なので

    $$ P[X=1]=0.3 $$

    $$ P[X=0]=1-0.3=0.7 $$

となります。

二項分布

ベルヌーイ試行を複数回行い、成功した回数Xが従う分布のことを「二項分布」といいます。

n回のベルヌーイ試行を行い、k回成功する（X = k）確率を次の式で表します。

    $$ P[X=k]={_n}C{_k}p^{k}(1-p)^{(n-k)} $$

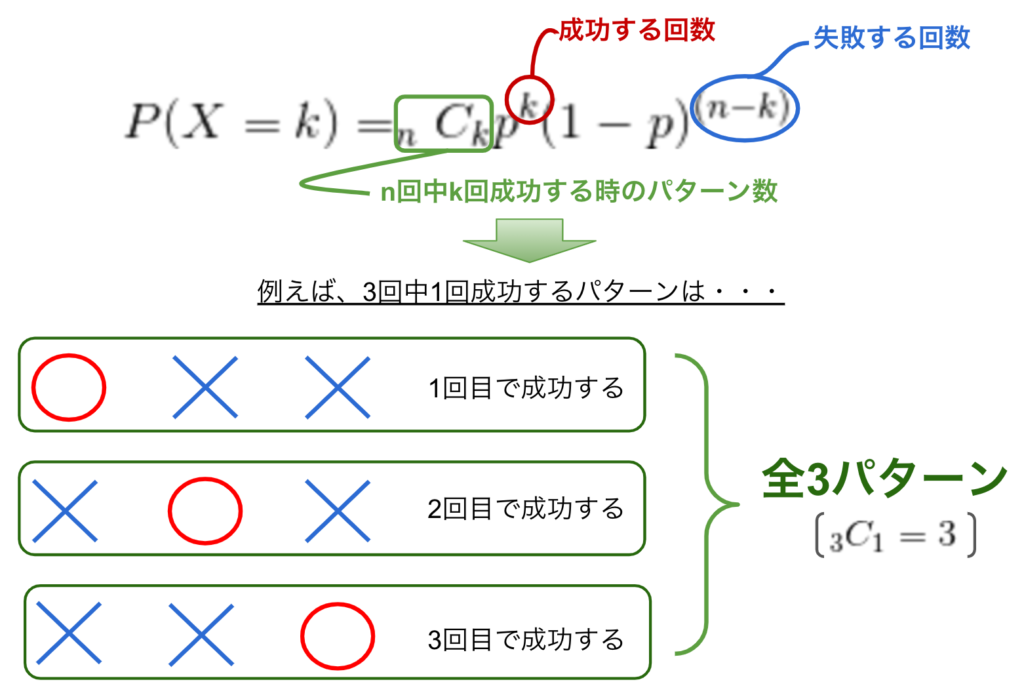
例えば、「コインを６回投げたときX回表になる確率」は

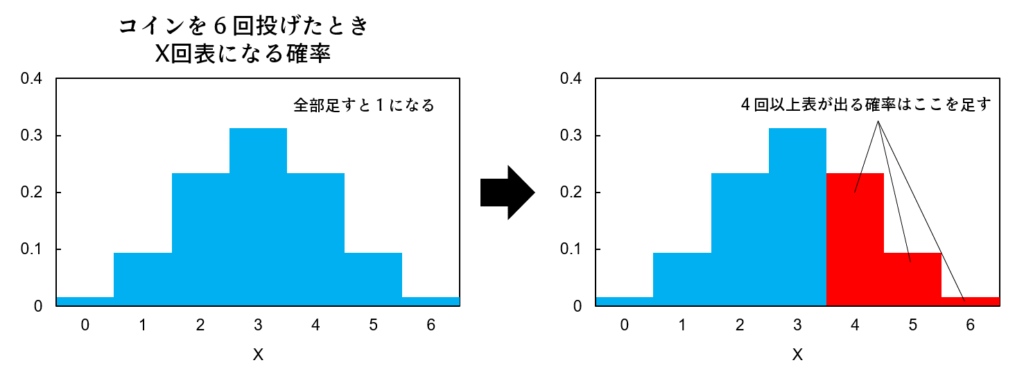
となります。「４回以上表が出る確率」は赤い棒を足し合わせた0.344です。34.4%ということはさほど珍しい事象ではなさそうです。

二項検定では、こういった事象の確率が例えば１％未満かどうかを調べて、１％未満であれば「異常にレアな事象である」「なにかおかしい」「明らかに偏りがある」「やっぱり差がある」という判断ができます。

有意水準

有意水準とは、統計的仮説検定において誤りを起こしてしまう確率のことで、平たく言えば「偶然じゃないよね？やっぱり差があるよね？」というボーダーラインです。 さっき登場した１％のことです。一般的にαで表し、α＝0.05 もしくは α＝0.01 と設定することが多いです。最近のトレンドは α＝0.01 なので今回はこれで話を進めていくことにします。

二項分布の平均と分散

試行回数をn、成功確率をpとした時の二項分布の平均と分散はそれぞれ以下の通りになります。

平均

    $$ E=np $$

分散

    $$ V=np(1-p) $$

Z検定とは

こちらは「正規分布を用いた統計的仮説検定」です。

以下の式にしたがって「検定統計量」というものを算出します。検定統計量は検定するためのなんか値と思ってください。

    $$ z=\frac{X-np}{\sqrt{np(1-p)}} $$

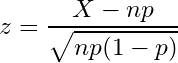
分子のnpは二項検定で登場した平均、分母の根号の中は分散と同じ形をしています。Xには対象としている確率変数が入ります。

ここで標準正規分布を用意します。

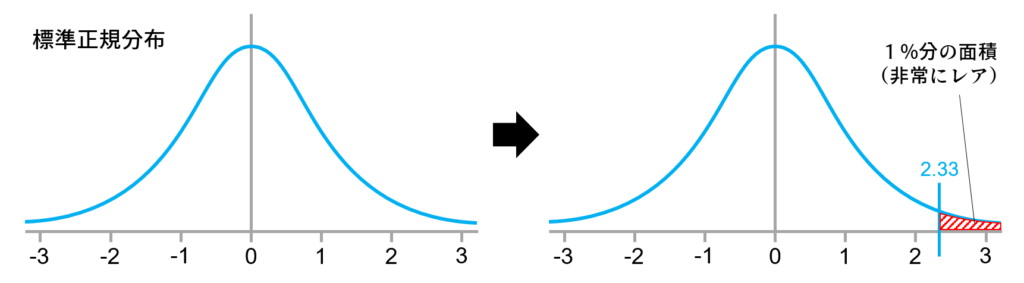
この分布は積分すると１になるのですが、ある事象がこの分布のどれぐらい端に当たるのかなぁというのを見るのがZ検定です。図の青い線（2.33）は最近のトレンドである有意水準α＝0.01に対応した値です（片側検定の場合）。この数字は覚えておくと良いでしょう。

Z検定では、ある事象の検定統計量が基準値（有意水準α＝0.01であれば2.33または-2.33）よりも外側にあるかどうかを調べて、外側にあれば「異常にレアな事象である」「やっぱり差があるよね」という判断ができます。

３タテは珍しいのか？

二項検定

単純に３タテされる（命中率30%の技を３回打って３回とも当たる）確率を求めてみましょう。

    $$ 0.3 \times 0.3 \times 0.3=0.027(=2.7\%) $$

二項分布の式に p = 0.3, n = 3, X =3 を代入しても同じ値が出ます。「３回当たる」確率だけなので、いくつかの棒を足し合わせる必要もありません。

2.7%ということは100回やって２～３回くらい発生する事象なので、あり得なくはないかなぁ・・・という感じです。デレステでSSRを１回で引き当てるようなもの です。（2020年2月現在SSRは３%）

余談ですが、３回一撃必殺技を放って、０回当たる確率〜３回当たる確率は

０回

    $$ P[X=0]={_3}C{_0} \times 0.3^{0} \times 0.7^{3}=0.343 $$

１回

    $$ P[X=1]={_3}C{_1} \times 0.3^{1} \times 0.7^{2}=0.441 $$

２回

    $$ P[X=2]={_3}C{_2} \times 0.3^{2} \times 0.7^{1}=0.189 $$

３回

    $$ P[X=3]={_3}C{_3} \times 0.3^{3} \times 0.7^{0}=0.027 $$

すべての事象の確率を足し合わせるとちゃんと１になります。（コルモゴロフの公理→第二公理）

    \begin{equation*} \begin{split} &P[X=0]+P[X=1]+P[X=2]+P[X=3]\nonumber\\ &=0.343+0.441+0.189+0.027\nonumber\\ &=1.0\nonumber \end{split} \end{equation*}

Z検定

「命中率30%の技を３回打って３回とも当たる」なので、検定統計量の式に p = 0.3, n = 3, X =3 を代入します。

    \begin{equation*} \begin{split} &z=\frac{X-np}{\sqrt{np(1-p)}}\\ &=\frac{3-3 \times 0.3}{\sqrt{3 \times 0.3 \times (1-0.3)}}\\ &= \frac{3-0.9}{\sqrt{0.63}}\\ &\fallingdotseq2.646 \end{split} \end{equation*}

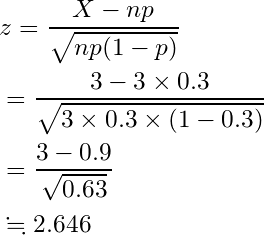
検定統計量を標準正規分布に当てはめてみます。

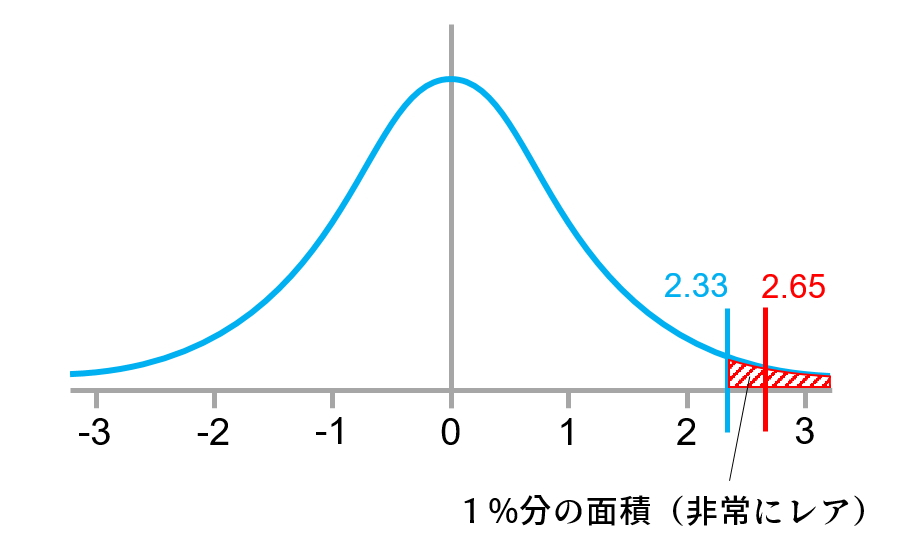
青い線よりも外側に赤い線があるので「100回に１回くらいしか起きない異常にレアな事象であり、偶然とは思えない（＝バグがある）」と主張できます。

よって、「一撃必殺技が当たりやすくなるバグがある」ことを主張しソフトの返品を要求できます。そして「そんなの確率だし、100回連続で当たることだってありますよ」と言われて突き返されます。

二項検定とZ検定で異なる結果が出た！？

二項検定では「まあ２～３%くらいの確率で起きる事象じゃん」、Z検定では「１％未満の確率でしか起きない」と矛盾した結果が出ました。この理由はだいたい

  • 二項分布（確率質量）を正規分布で近似しちゃっていいの？
  • nやpが小さいときは誤差大きいよね？

と見られています。次の図で雰囲気だけ理解してください。

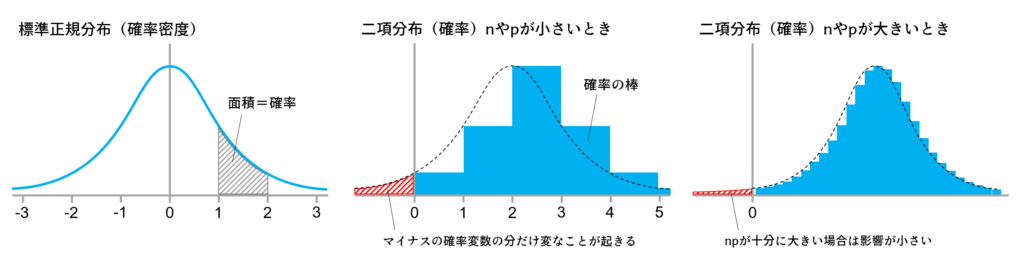
np＜５くらいのときはZ検定を使わず、素直に確率を計算して二項検定するのがいいでしょう。逆にnpが十分に大きいときは確率の計算と棒の足し合わせが大変なので、標準正規分布で近似したZ検定に任せるのがいいでしょう。

おまけ

デレステで爆死した人の話

このサイトで一番多くの記事を書いている人間はガチャ運がないことで有名で（？）、2015年の年末にデレステで180連してSSRが一枚も出なかったためアンインストールし、ショックから立ち直れずに年始に機種変をしたという噂があります。当時はSSRが1.5%でしたが、年末年始の「SSR出現率２倍キャンペーン」に、貯めておいた無課金スタージュエル180個をぶっ込んだとのことです。

Z検定的には、検定統計量に p = 0.03, n = 180, X = 0 を代入するとこうなります。

    \begin{equation*} \begin{split} &z=\frac{X-np}{\sqrt{np(1-p)}}\\ &=\frac{0-180 \times 0.03}{\sqrt{180 \times 0.03 \times 0.97}}\\ &\fallingdotseq-2.359 \end{split} \end{equation*}

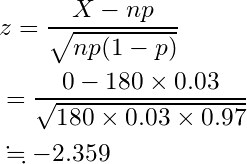
マイナスの値のときは-2.33よりも外側にあるかを見ます。検定統計量が-2.33を下回っているので、こちらも偶然とは思えない事象であることが分かりました。ガチャ確率の操作が疑われます。それか、無償ジュエルは有償ジュエルよりも確率を低く操作しているかもしれません。

何回連続で出なければ不正を疑える？

180連してSSRが１枚も出なければガチャ確率の操作を疑えることが分かりましたが、果たして最低何連して出なければおかしい事象だと言えるでしょうか。

検定統計量が-2.33を下回れば良いので、以下の式を解きます。

    \begin{equation*} \begin{split} z=\frac{X-np}{\sqrt{np(1-p)}}=\frac{0-0.03n}{\sqrt{0.0291n}}<-2.33 \end{split} \end{equation*}

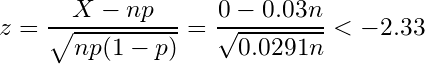
nについて解くと

    $$ 175.53<n $$

つまり、176回連続でSSRが出なかった場合は運営にクレームを入れていいです。

とはいえ確率というのは困ったもので、「100万連してSSRが１枚も出なかった」としても「まあそういう確率だってありますよね？」と言われれば何も反論できません…。

ちなみに、二項検定的には176連して出ない確率は0.97176＝0.47%であり、この数字は絶対的に正しいです。しかしZ検定的には「100回に１回くらい発生するレアな事象（＝1%）」という解釈になります。（片側・両側の話は別にしても）やはり少し違う結果となります。

おまけ２

ちなみに同氏は2019年末のミスタードーナツ福袋を７つ買い、２種類がランダムに入っているというブランケットとエコバッグがどちらも一方しか当たりませんでした。

気になる方はこれについても検定を行ってみてはいかがでしょうか。

タイトルとURLをコピーしました