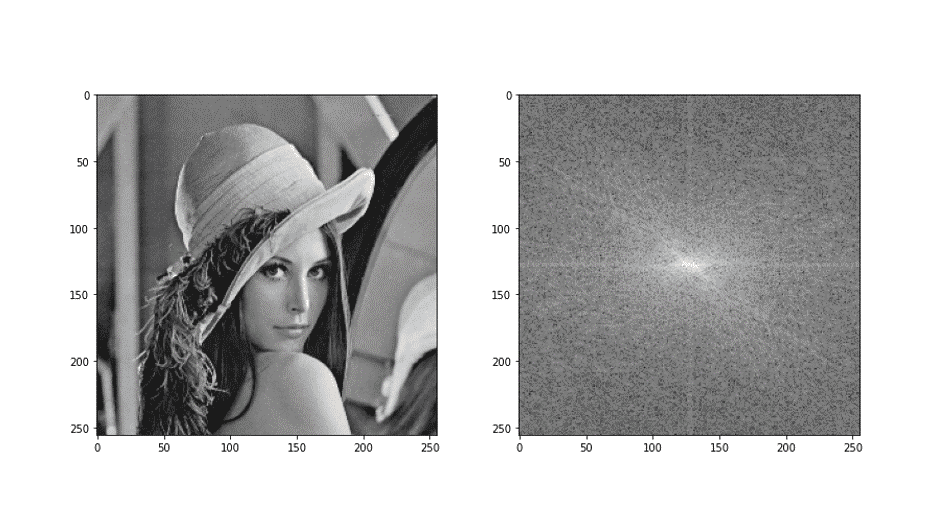
やること
あらゆる波形や模様は複数の波の合成によって表現できると考え、素材となっている波の周波数成分を求める方法をフーリエ変換と呼びます。Pythonにもフーリエ変換の関数が用意されていますので、画像のフーリエ変換を試してみましょう。
実行環境
WinPython3.6をおすすめしています。
Google Colaboratoryが利用可能です。

参考文献
画像に対する高速フーリエ変換関数 np.fft.fft2() の使い方についてはこちらをご参照ください。
また、こちらのサイトでは画像とスペクトル空間の関係が視覚的・直感的に分かります。
こちらの動画もわかりやすいです。
使用した画像
御年70歳のレナ・ソーダバーグさんをお借りします。

コード
まず、フーリエ変換と逆フーリエ変換の関数です。
#フーリエ変換
def FFT(img):
#フーリエ変換
fimg = np.fft.fft2(img)
fimg = np.fft.fftshift(fimg) #低周波成分を中央に寄せる
#符号を保ったまま対数処理
real = fimg.real
real[real>0] = np.log10(real[real>0])
real[real<0] = -np.log10(-real[real<0])
imag = fimg.imag
imag[imag>0] = np.log10(imag[imag>0])
imag[imag<0] = -np.log10(-imag[imag<0])
return real, imag
#逆フーリエ変換
def IFFT(real, imag):
#符号を保ったまま指数処理
real[real>0] = 10**real[real>0]
real[real<0] = -10**(-real[real<0])
imag[imag>0] = 10**imag[imag>0]
imag[imag<0] = -10**(-imag[imag<0])
#複素数行列
fimg = np.zeros(real.shape, np.complex128)
fimg.real = real
fimg.imag = imag
#逆フーリエ変換
fimg = np.fft.ifftshift(fimg)
img = np.fft.ifft2(fimg)
img = img.real
img = img.clip(0, 255).astype(np.uint8)
return imgグレースケール画像をフーリエ変換すると複素数行列が得られ、これは実部行列と虚部行列の2チャンネルから成ります。それぞれの型は以下のようです。
| 行列 | コード中の変数名 | ndarray型 |
| 複素数行列 | fimg | np.complex128 |
| 実部(fimg.real) | real | np.float64 |
| 虚部(fimg.imag) | imag | np.float64 |
逆フーリエ変換については単純に逆のことをしているだけです。
次に、普通の画像の表示関数と、FFT画像(=周波数成分の画像。呼び方合っていますか?)の表示関数です。FFT画像の表示については、実部行列と虚部行列の2つをどうやって可視化すれば良いか戸惑います。ここでは複素数型np.complex128に格納してから絶対値を取ることで画像らしく表示させています。この処理には他の流派もあるそうですが、可視化できれば何でも構わないと思います。
#画像の表示関数
def show(img):
plt.figure()
plt.imshow(img)
plt.gray()
plt.show()
#FFT画像の表示関数
def showfft(real, imag):
fimg = np.zeros(real.shape, np.complex128)
fimg.real = real
fimg.imag = imag
img = np.abs(fimg)
plt.figure()
plt.imshow(img)
plt.gray()
plt.show()では、レナさんをフーリエ変換してそのまま逆フーリエ変換してみましょう。
#グレースケール読み込み
img = cv2.imread('25-1_sample.png', 0)
show(img)
#フーリエ変換
real, imag = FFT(img)
showfft(real, imag)
#逆フーリエ変換
img = IFFT(real, imag)
show(img)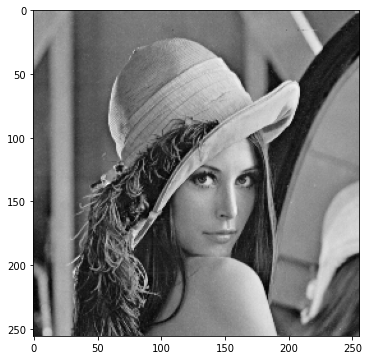
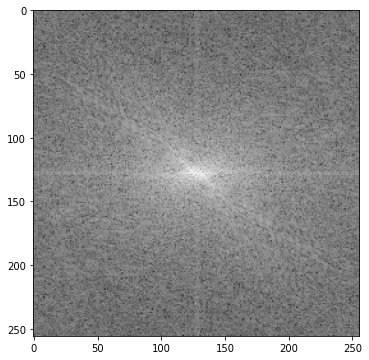

FFT画像が表示され、逆フーリエ変換すると元の画像に戻ることが確認できました。FFT画像は白い点が1つの周波数成分(1つのsin波)を表しています。
FFT画像と周波数成分の関係
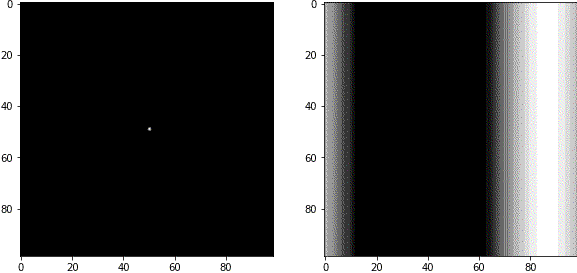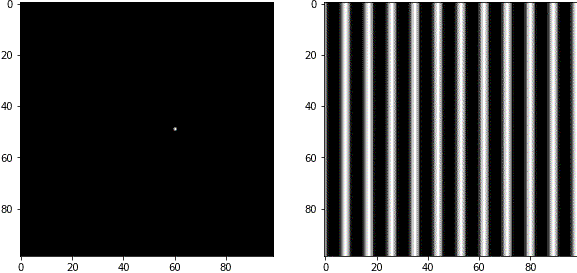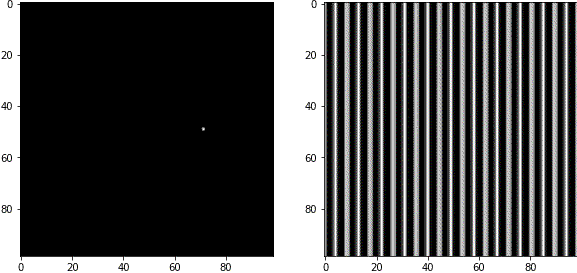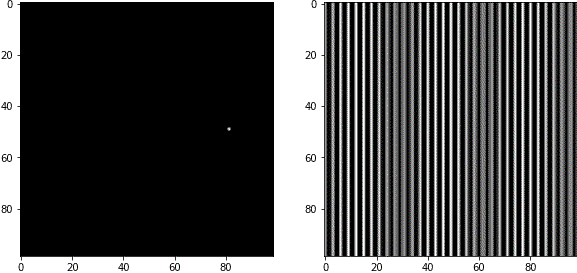
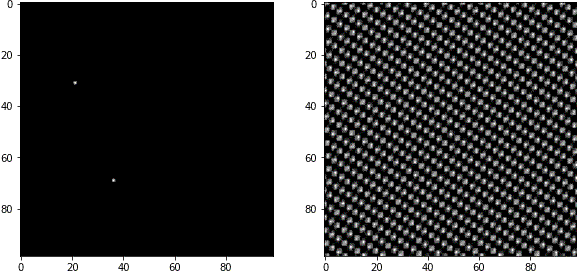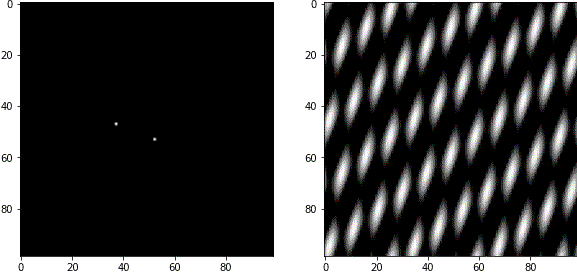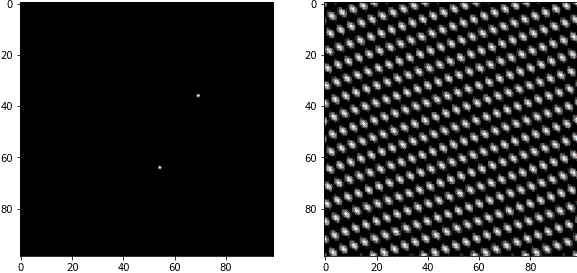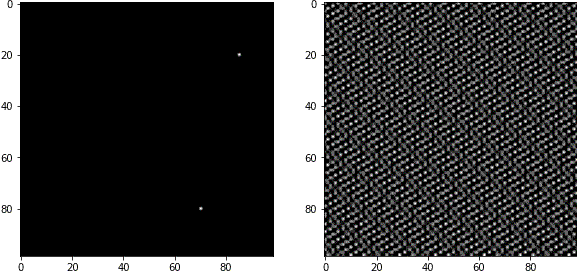
FFT画像と周波数成分の関係が理解しやすいようにGIF動画を作りました。左側がFFT画像で、白いピクセルの部分の周波数成分を持っています。右側が逆フーリエ変換後の画像で、波が合成された結果が見えます。
例1
FFT画像は中心部が低周波成分(粗い波)、周辺部が高周波成分(細かい波)を表します。
例2
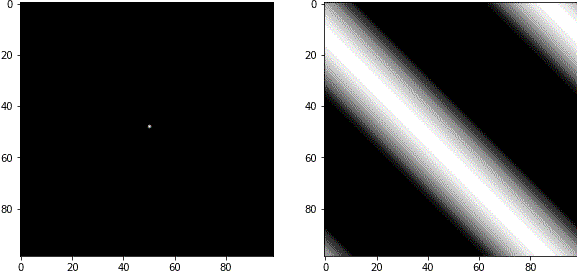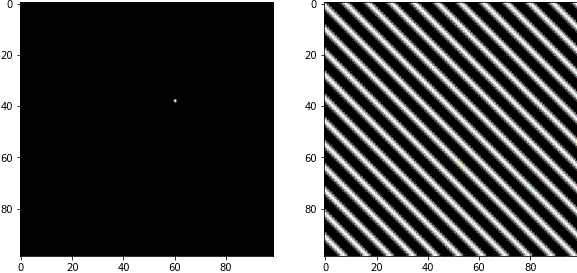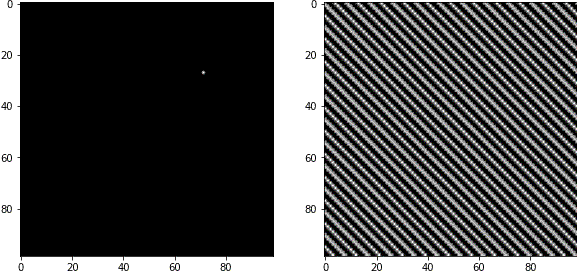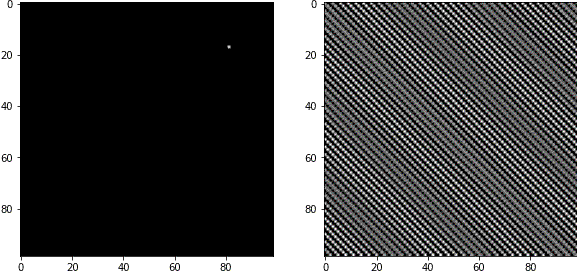
白いピクセルの中心から見た角度は、波の角度に対応しています。
例3
複数のピクセルを白く塗ると、複数の波の合成が表現できます。
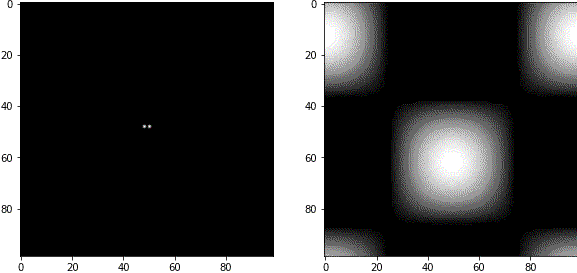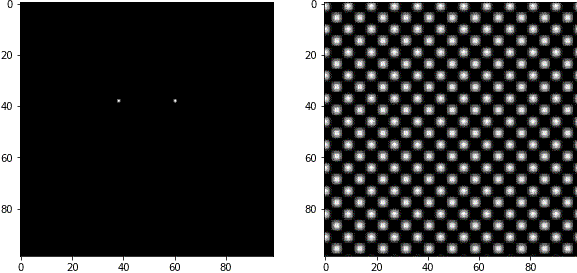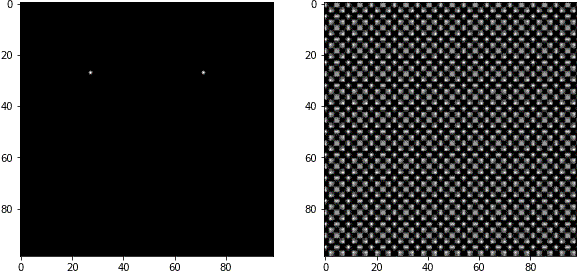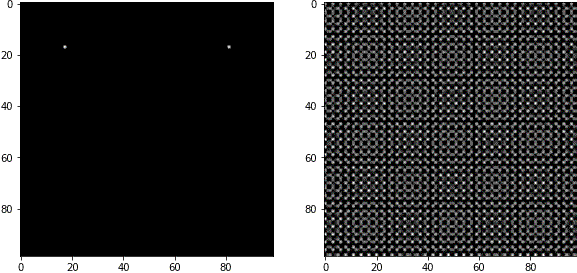
例4
ここでは2つの波の合成に留めますが、このようにしてあらゆる画像が表現できます。ただしFFT画像を編集して狙った画像を構築するのはおそらく不可能です。
周波数成分のカット
最後に、FFT画像の一部をカット(黒塗り)するとどうなるか見てみましょう。
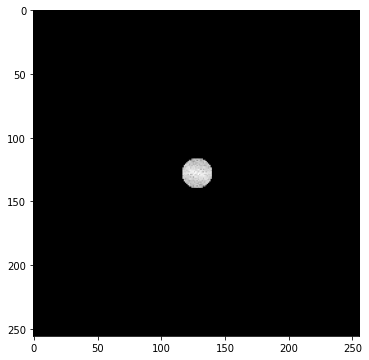
ローパス(低周波を残す)
FFT画像の中心部は低周波成分でした。これだけを残すように周辺部を黒塗りにすると、画像はぼやけてしまいました。粗い波の合成では細部まで表現できないためです。
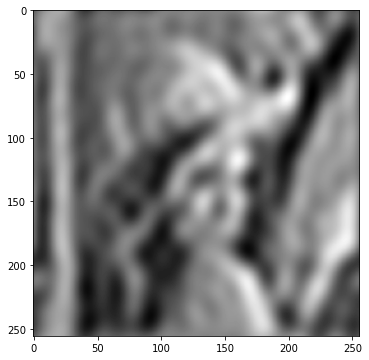
ハイパス(高周波を残す)
逆に低周波成分を取り除くと、画像全体が暗くなり、線がゆらゆらした感じになりました。これを上手く解説できる方いらっしゃいますでしょうか。


おわりに
Pythonをやっていて複素数が出てくるとは思いませんでした。複素数の計算は難しいですが、表示だけなのでなんとかなりました。