概要
「身長-体重=110が標準体型」というスペ110理論があります。この「身長-体重」をスペック値と呼ぶそうです。
しかし、私たちが体型を評価する指標として習ったのはBMI(Body Mass Index)だったと思います。
身長T [cm]を用いて体重W [kg]を表すと、
BMIの標準体型は(BMI=22のとき)
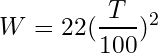
スペ110理論は
![]()
となりますが、どうしてTの2乗の式だったものが1乗(=比例)でもOKということになっているのでしょうか?数学的に考察してみます。
とりあえずグラフで見てみる
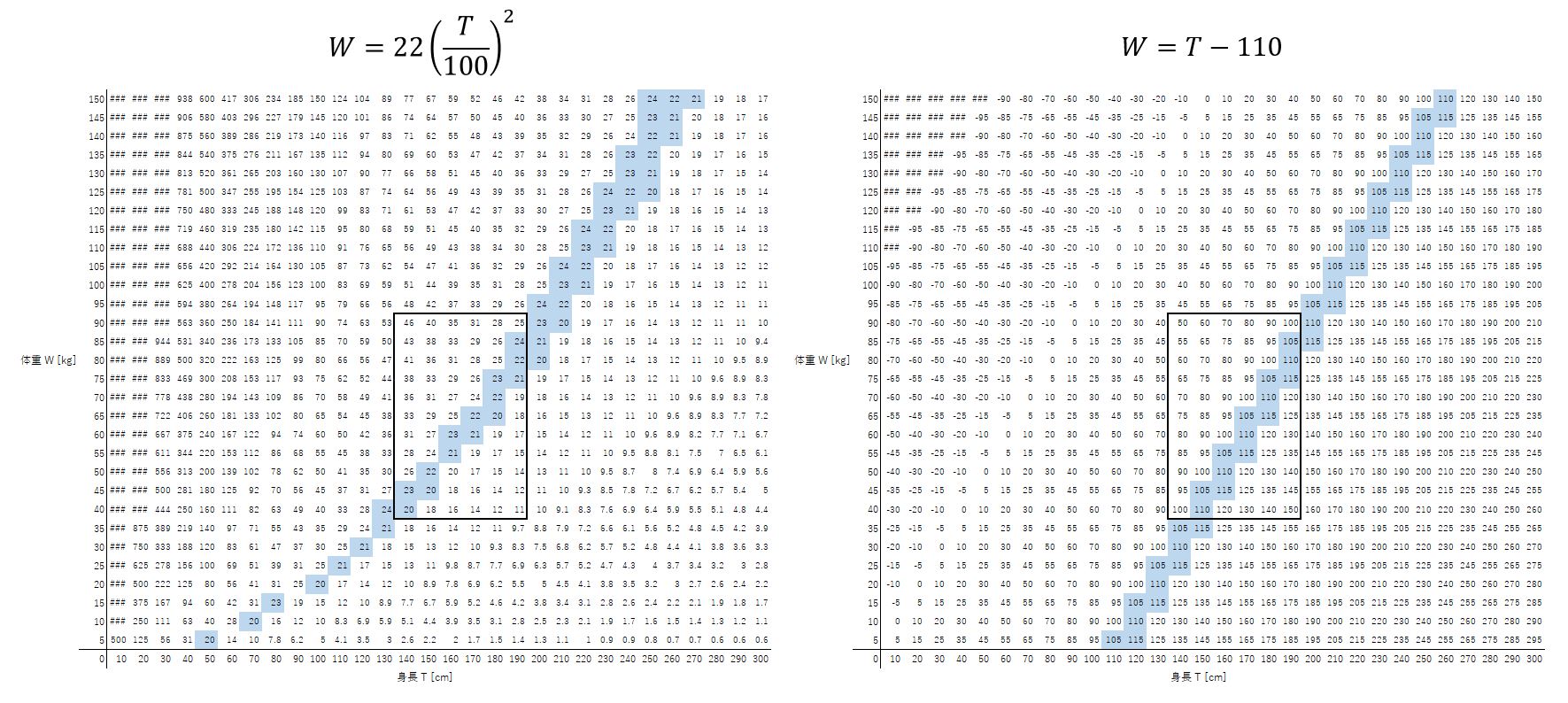
Excelでそれぞれ簡易的に可視化してみました。横軸は身長10~300 [cm]まで、縦軸は体重5~150 [kg]です。左はBMI理論のBMI=22付近を、右はスペ110理論のスペック値=110付近を色付けしました。
やはりTの2乗と1乗で間違いありません。しかし、太枠で示した「大多数の人が当てはまる身長・体重の範囲(身長140~190 [cm]、体重40~90 [kg])」に限って見れば、ほとんど直線で近似できている(?)ことがわかります。
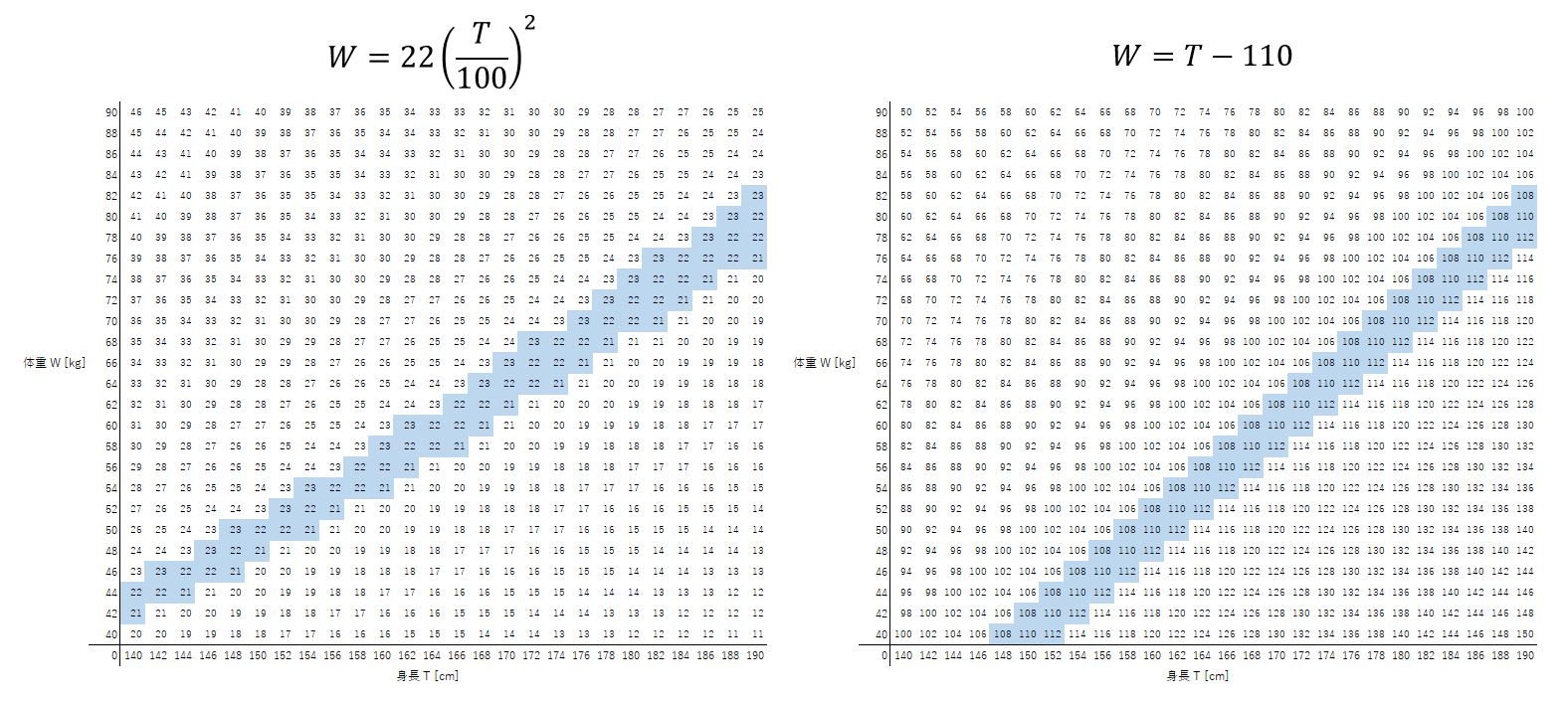
この範囲を拡大してみました。
身長が低めの領域ほど乖離していますが、だいたい直線でええやろ、ということですね。
結論としては、
- 「BMI=22が標準体型」を前提とした場合に
- BMIだと割り算の暗算ができないよ~ピエン(><)パオン
- せや、足し算か引き算で近似しよう
- 「身長-体重=110が標準体型」でええか
という面倒くさがり屋の仕業だと分かりました。
もっと深掘りしてみる①
せっかくなのでもう少し深掘りしてみましょう。
「スペ理論(引き算)でBMI標準体型をよく近似できるのはどんな身長・体重の人か?」を考えてみます。
もっともよく適用できる(近似できる)領域とは線の傾きが近い領域のことですから、それぞれ微分して、
BMIの式の傾き
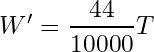
スペ理論の式の傾き(というか傾き1でなければ暗算できないから)
![]()
これが一致するということで T=227 [cm] (W=115 [kg])より、「身長227cm、体重115kg付近の標準体型の人であればスペ理論がよく適用できる」ことが分かりました。
いやしかし、これでは使いようがありません。。(;´Д`)
2024/05/11追記
Twitterで面白いコメントを頂きました!
「BMIの式をテイラー展開したらスペック理論が導けるのではないか?」
なんじゃそりゃ!早速やってみましょう。
BMIの式をTの関数と見て、T=t(tは適当な身長)のまわりで第二項までテイラー展開します。つまりTの1乗項が出現するまでですね。
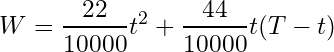
整理すると
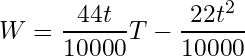
ここでTの係数が1(なぜならそうでないと暗算できないから)になることから t=227 [cm] が導け、このときの第二項は-114 [cm] となります。つまりBMIのテイラー展開からも、身長227cm付近限定ではあるものの、W=T-114というほぼスペック理論な近似式が導けるのです。工エエェェ(´д`)ェェエエ工
※注意:T=227のまわりでテイラー展開したので身長227cmの人に当てはまる話です。身長が227cmから離れるほど近似精度が悪くなっていくので一般人には適用できません。
これでは使いようがありません。。(;´Д`)(2回目)
もっと深掘りしてみる②
そこで方針を変えて、「身長165cm(男女混合平均)付近においてスペ理論(引き算)でよく近似できる体型はどんなBMIか?」を考えます。
BMI値をBとすると、Bによって線の傾きは変わるので
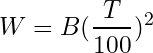
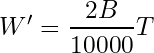
これがT=165 [cm]において1と等しいことから
![]()
このBMIに対応する体重は W=82 [kg] で、このときのスペック値は83なので、結局「身長165cm、体重82kg付近のやや肥満の人であればスペ83理論がよく適用できる」ことがわかります。BMI=30は肥満1度と肥満2度の境界です。
分かりやすくスペック値80として実用的に言い換えると、
身長-体重=80は肥満2度
おわりに
「スペ80理論」使える場面あるんですかねぇ(´-﹏-`;)