5-4. ３次元空間上のねじれた２直線の最接近点を求める

数理モデル / 論理

2020/05/30

やること
参考文献
実行環境
pip, import
コードと解説

やること

皆さんも、３次元空間上のねじれ関係にある２直線の最接近点が求められなくて枕を濡らした夜があるかと思います。私もあります。

問題

次の２直線を最短で結ぶ線分の両端の座標を求めよ。

　直線１　点(-1, 1, 1)を通りベクトル(1, 0, -1)の直線
　直線２　点(0, 3, 2)を通りベクトル(1, 2, -1)の直線

この問題はやってみると途中で「２変数の最適化問題っぽいな…遺伝的アルゴリズムでいけるやん！」と思ってしまうのですが、いくらGA信者でもさすがにそれはまずいという天の声が聞こえましたので、きちんと解析的に解きます。

解析的に解くとは言いましたが、紙とペンでとは言っていませんので、Pythonを使って解きます。

参考文献

問題はこちらをそのまま使用させていただきました。感謝申し上げます。

ねじれの位置にある2直線間の最短距離（共通垂線）

定期試験・大学入試対策に特化した解説。直線を媒介変数表示にすると2変数関数の最小問題に帰着する。

Sympyの使い方はこちらにまとまっています。

Python, SymPyの使い方（因数分解、方程式、微分積分など） | note.nkmk.me

SymPyは代数計算（数式処理）を行うPythonのライブラリ。因数分解したり、方程式（連立方程式）を解いたり、微分積分を計算したりすることができる。公式サイト: SymPy ここでは、SymPyの基本的な使い方として、 ...

実行環境

WinPython3.6をおすすめしています。

WinPython - Browse /WinPython_3.6/3.6.7.0 at SourceForge.net

Portable Scientific Python 2/3 32/64bit Distribution for Windows

Google Colaboratoryが利用可能です。

Google Colab

pip, import

Sympyという数式処理用のライブラリを用います。中学校や高校で習ったような連立方程式や微分積分を一瞬で解いてくれます。

import numpy as np
import sympy

コードと解説

各点と各ベクトルを次のように表します。

$\begin{equation*} \begin{split} &p = (-1, 1, 1), \; v = (1, 0, -1)\nonumber\\ &q = (0, 3, 2), \;w = (1, 2, -1) \end{split} \end{equation*}$

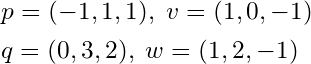
数式１を「変数 s によって動く点 P の集合」として表現します。同様に、数式２は変数 t を使って点 Q の集合として表現します。

$\begin{equation*} \begin{split} P &= (p_0 + sv_0, p_1 + sv_1, p_2 + sv_2)\nonumber\\ &= (-1 + 1s, 1 + 0s, 1 - 1s) \end{split} \end{equation*}$

$\begin{equation*} \begin{split} Q &= (q_0 + tw_0, q_1 + tw_1, q_2 + tw_2)\nonumber\\ &= (0 + 1s, 3 + 2s, 2 - 1s) \end{split} \end{equation*}$

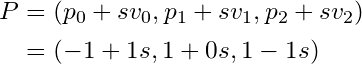
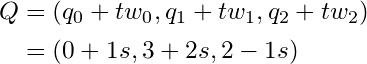
#直線１を表す点とベクトル
p = np.array([-1, 1, 1])
v = np.array([1, 0, -1])

#直線２を表す点とベクトル
q = np.array([0, 3, 2])
w = np.array([1, 2, -1])

#変数s, tを用意
s = sympy.Symbol('s')
t = sympy.Symbol('t') #ここからs, tは通常の変数ではなく記号として扱う

"""
直線１を成す点Pの座標は次の通り
    (x, y, z) = (p[0]+s*v[0], p[1]+s*v[1], p[2]+s*v[2])
直線２を成す点Qの座標は次の通り
    (x, y, z) = (q[0]+t*w[0], q[1]+r*w[1], q[2]+r*w[2])
"""

点 P のと点 Q の距離を表します。ただし処理を楽にするため、距離の２乗を表すことにします。

$\begin{equation*} \begin{split} PQ^2 &= ( (q_0+tw_0) - (p_0+sv_0) )^2\nonumber\\ &+ ( (q_1+tw_1) - (p_1+sv_1) )^2\nonumber\\ &+ ( (q_2+tw_2) - (p_2+sv_2) )^2\nonumber\\ &= ( (0+1s)-(-1+1s) )^2 + ((3+2s)-(1+0s) )^2 + ((2-1s)-(1-1s) )^2 \end{split} \end{equation*}$

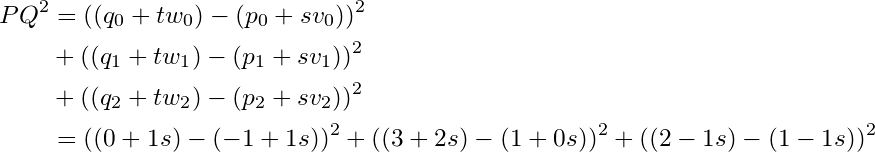
#点Pと点Qの距離の２乗
PQ2 = ( (q[0]+t*w[0]) - (p[0]+s*v[0]) )**2\
     +( (q[1]+t*w[1]) - (p[1]+s*v[1]) )**2\
     +( (q[2]+t*w[2]) - (p[2]+s*v[2]) )**2

これが最小になるような s, t の組み合わせを見つければよいわけです。数学の問題として具体的に点とベクトルが与えられている場合は、式を整理して平方完成して…という手順です。

しかし、どんな点とベクトルが来ても良いように一般化してプログラムで解くことを目指します。

この式を s, t でそれぞれ偏微分します。

$\begin{equation*} \begin{split} &\frac{\partial PQ^2}{\partial s} = ???\nonumber\\ &\frac{\partial PQ^2}{\partial t} = ??? \end{split} \end{equation*}$

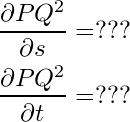
#これを偏微分
dPQ2_ds = sympy.diff(PQ2, s)
dPQ2_dt = sympy.diff(PQ2, t)
print('dPQ2/ds = {}'.format(dPQ2_ds))
print('dPQ2/dt = {}'.format(dPQ2_dt))

dPQ2/ds = 4*s - 4*t　・・・①
dPQ2/dt = -4*s + 12*t + 8　・・・②

さっそく紙とペンでの計算を諦めてしまったわけですが、Pythonはきちんと偏微分してくれました。

ここで、これらの式の意味を考えます。偏導関数①はある s におけるPQ間の距離の増減を意味しており、それは s と t によって変わると言っています。同様に、偏導関数②はある t におけるPQ間の距離の傾きを意味しており、やはり s と t によって変わると言っています。

ここでコーヒーを飲んで空間想像力を発揮させます。直線１上のどこかに点 P を固定して、直線２上を点 Q が左の果てから右の果てへ通過していくことをイメージすると、PQ間の距離は長い～短い～長いと変化します。よってPQは下に凸であり、傾き＝０すなわち偏導関数①＝０のときに最短となることが想像できます。そして下線の性質は s, t によらず必ず成立します。ただしその地点は s と t によって変わります。これは相手から見た場合にも同じことが言えます。s と t によるが、偏導関数②＝０のときに最短距離を迎えます。

これらをあわせると、２つの変数によって変わる２つの偏導関数がともに＝０を満たすときに線分PQは最小となります。（証明にはなっていませんが、感覚で攻めていきます。。）

よって、

$\begin{equation*} \begin{split} &\frac{\partial PQ^2}{\partial s} = 0\nonumber\\ &\frac{\partial PQ^2}{\partial t} = 0 \end{split} \end{equation*}$

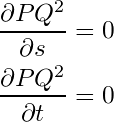
を満たす s, t を見つければよいことがわかります。よく見るとこれらは２元連立１次方程式ですので、中学生が得意とするやつです。

#偏導関数＝０を連立方程式として解く
ans = sympy.solve([dPQ2_ds, dPQ2_dt])
print('ans = {}'.format(ans))
s, t = ans[s], ans[t] #ここでs, tは通常の変数に戻る
print('(s, t) = ({}, {})'.format(s, t))

""""
最接近時のs, tが求められた
"""

ans = {s: -1, t: -1}
(s, t) = (-1, -1)

あとは直線１上の点 P に s を、直線２上の点 Q に t を、それぞれ代入してやると最接近点が分かります。最接近距離も式を再利用して求められます。

#それは直線１上のどこなのか
x, y, z = p[0]+s*v[0], p[1]+s*v[1], p[2]+s*v[2]
print('On line 1 : (x, y, z) = ({}, {}, {})'.format(x, y, z))
#それは直線２上のどこなのか
x, y, z = q[0]+t*w[0], q[1]+t*w[1], q[2]+t*w[2]
print('On line 2 : (x, y, z) = ({}, {}, {})'.format(x, y, z))

#最接近距離
PQ2 = ( (q[0]+t*w[0]) - (p[0]+s*v[0]) )**2\
     +( (q[1]+t*w[1]) - (p[1]+s*v[1]) )**2\
     +( (q[2]+t*w[2]) - (p[2]+s*v[2]) )**2
PQ = PQ2**0.5
print('min distance = {}'.format(PQ))

On line 1 : (x, y, z) = (-2, 1, 2)
On line 2 : (x, y, z) = (-1, 1, 3)
min distance = 1.41421356237310

最接近距離は、手計算では√２になるようです。1.41421356237310でも実用上問題ありませんが、この後にいろいろな計算を続けると桁落ちや丸め誤差が出てくるかもしれません。これはプログラミングの宿命であり、手計算をサボった代償なのであります。

最後に、結果を３Dプロットしました。