やること
Pythonのパッケージ(pip install するやつ)を作っていたら、パッケージに画像ファイルを含めるのが大変だということが分かりました。
そこで「プログラム中に画像を埋め込めばいっか」と思ったので、試してみます。
実行環境
WinPython3.6をおすすめしています。

WinPython - Browse /WinPython_3.6/3.6.7.0 at SourceForge.net
Portable Scientific Python 2/3 32/64bit Distribution for Windows
Google Colaboratoryが利用可能です。

Google Colab
使用した画像
48*48サイズの手まり寿司の画像を用意しました。4chある透過画像です。
画像を文字列に変換する
画像を読み込んで、imarray = np.array(…) という文字列に変換します。文字列はコンソールに出力してコピペ取得してもよいのですが、長すぎてコンソールが流れてしまうので、imarray.py というプログラムファイルとして書き出しました。
from PIL import Image
import numpy as np
#画像読み込み
img = Image.open('14-14_temari.png').convert('RGBA'); img.close
#ndarrayに変換
array = np.array(img)
print(array.shape)
#テキストに変換
text = 'imarray = np.array(['
for i in range(len(array)):
text += '['
for j in range(1, len(array[0])):
text += '[{},{},{},{}],'.format(array[i, j, 0], array[i, j, 1], array[i, j, 2], array[i, j, 3])
text = text[:-1]
text += '],'
text = text[:-1]
text += '])'
#テキストの書き出し
with open('imarray.py', 'w') as f:
f.write(text)(48, 48, 4)出来上がった imarray.py を開くと、画像情報が3次元配列として imarray に代入されようとしています。
※ただし文字列が長すぎて激重のため開発環境がバグっても責任は負いかねます。
imarray = np.array([[[0,0,0,0], ... ,[0,0,0,0]]])画像の確認
この文字列をコード中に埋め込み、画像を読み込むことなく画像を表示します。
※繰り返しになりますが、開発環境がバグっても責任は負いかねます。
import numpy as np
from PIL import Image
import matplotlib.pyplot as plt
#配列
imarray = np.array([[[0,0,0,0], ... ,[0,0,0,0]]])
#image形式に変換(しなくてもplt.imshow()できるが)
img = Image.fromarray(np.uint8(imarray))
print(type(img))
#画像を確認
plt.imshow(img)
plt.show()<class 'PIL.Image.Image'>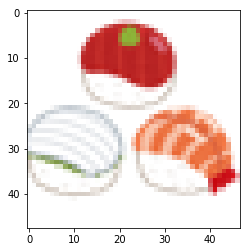
できました。
役に立つのか?
もともとの画像が9KBであるのに対し、文字列が書き込まれた imarray.py は31KBでした。圧縮していないのですから当然です。48*48サイズの画像情報でも開発環境の挙動が怪しくなりましたので、実用的ではなさそうです。残当