やること
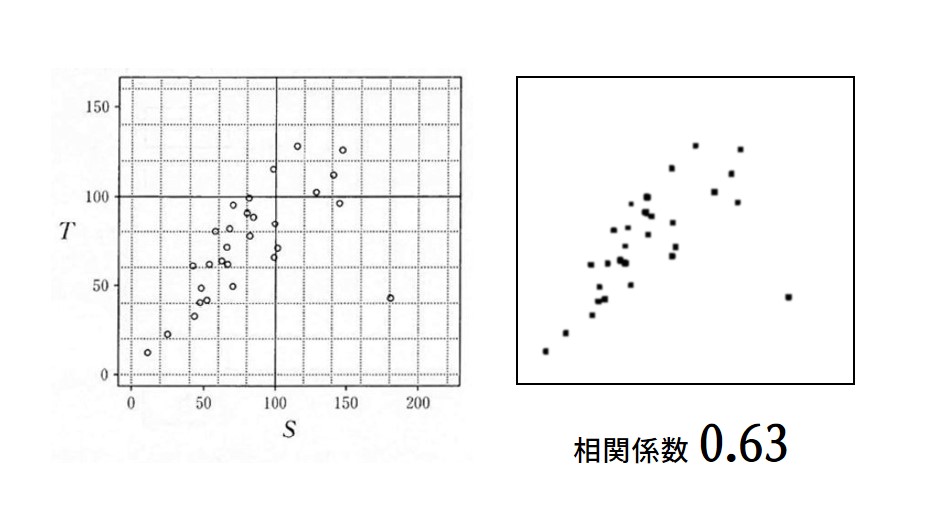
2022年共通テスト数学Ⅰ・数学Aのとある問題が話題になっています。簡単に言うと「相関係数が約0.63の散布図を選べ」というものです。
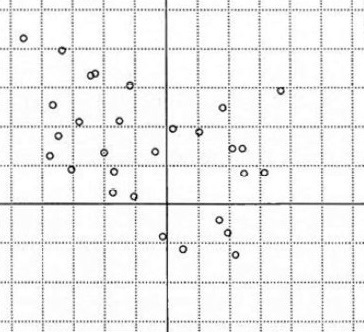
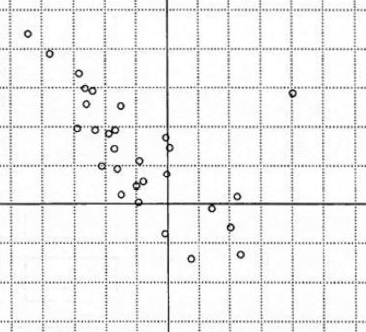
選択肢のグラフは4つあり、問題全文を確認するとSとTの平均値や標準偏差が与えられているため2つまでは容易に絞れるようです。しかし、選択肢②と③のどちらを選ぶかは迷った人が多かったようです。
ネット上では「勘しかないのか?」「点の座標を調べて計算したらいいんじゃね?」「正解はガクトが選んだほうです」といった意見が見られました。今回はPythonとImageJを駆使してこれらの選択肢の相関係数を求めてみましょう。
実行環境
WinPython3.6をおすすめしています。
そしておなじみのImageJ。バグが多いです。
準備
問題の画像がこちらです。
まずは座標の部分をトリミングします。このとき上下反転させておきます。最後にImageJで点の座標を解析する際、画像左上を原点として右側にx、下側にyを取りますので、このように上下反転させておけばそれぞれSとTに対応します。
さらにグラフ中の点(丸)を一つトリミングします。10×10pxになりました。
Pythonで点群のクリーニング
画像とマークをグレースケール画像として読み込み、白黒を反転させます。白が255で黒が0です。
import cv2
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
#ファイル名
img_file = '14-21_img1.jpg'
mark_file = '14-21_mark.jpg'
save_file = '14-21_save1.png'
#表示関数
def show(img):
plt.imshow(img)
plt.gray()
plt.show()
plt.close()
#画像とマークを読み込んで白黒反転
img = cv2.imread(img_file, 0)
img = 255 - img.astype(int)
show(img)
mark = cv2.imread(mark_file, 0)
mark = 255 - mark.astype(int)
show(mark)
次に、画像上をマークで二次元畳み込み演算します。マークがぴったり重なる部分は大きい値になります。最大値で規格化して画像として確認してみます。
#画像上をマークで畳み込みして0-1に規格化
over = signal.convolve2d(img, mark, mode='same', boundary='wrap')
print(np.max(over))
over = over / np.max(over)
print(np.max(over))
show(over)1230307
1.0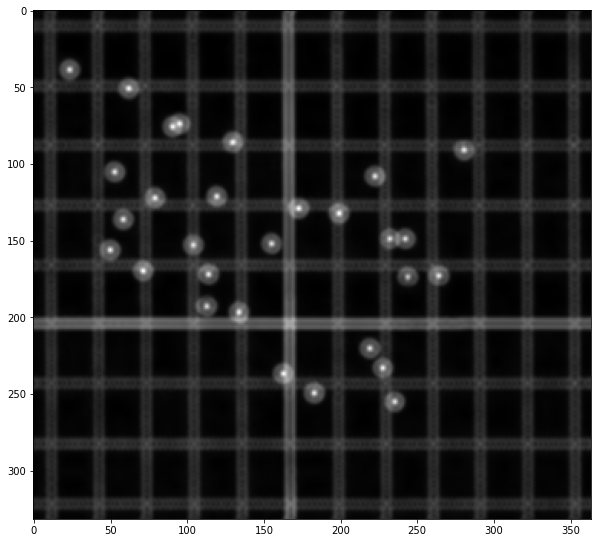
適当なしきい値で二値化して元の画像に重ね、正しく検出できているか目を凝らして確認します。
#適当なしきい値で二値化して画像化
over = (over > 0.74) * 255
show(over)
#元画像に重ねて確認
new = np.zeros((img.shape[0], img.shape[1], 3), int)
new[:, :, 0] = img // 2
new[:, :, 1] = img // 2
new[:, :, 2] = img // 2
new[over==255] = [255, 0, 0]
show(new)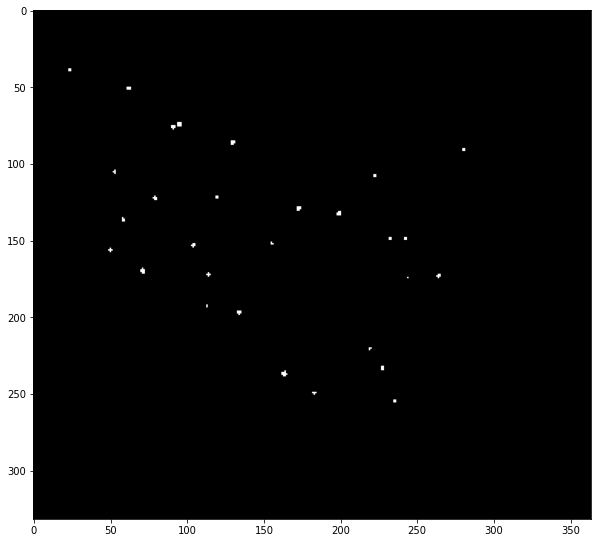
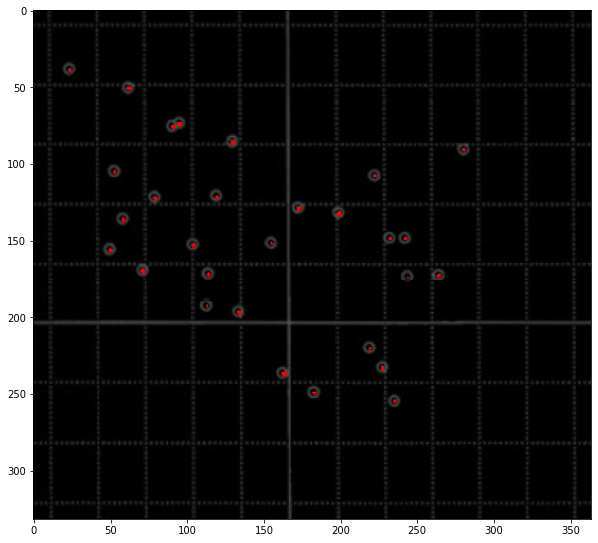
よければ二値化画像を保存します。
#よければ二値化画像を保存
cv2.imwrite(save_file, over)ImageJで点群の座標を取得
ImageJで読み込んだら、
- Process > Binary > Ultimate Points
- Image > Adjust > Threshold
で各点を1ピクセルに縮小します。

最後に
- Analyze > Analyze Particles
で各点の座標を取得し、Excelで相関係数を求めます。
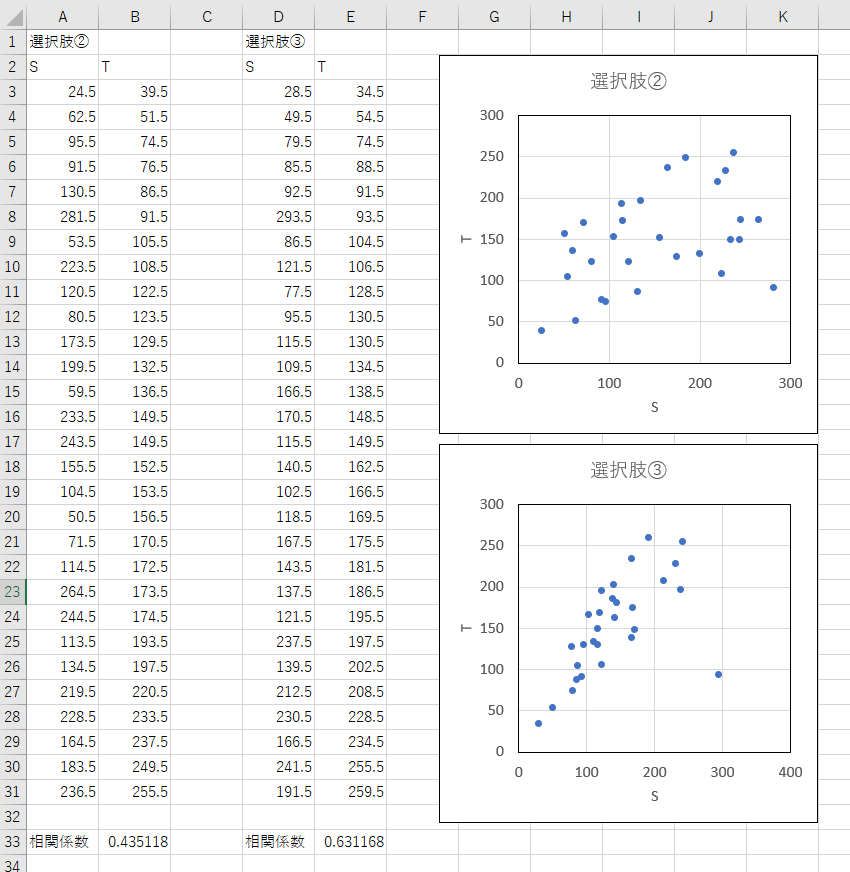
以上より、選択肢②は相関係数0.44、選択肢③は相関係数0.63でした。ただしこれは正確な値ではないことを次の項で説明します。
おまけ
問題のグラフとImageJで解析した座標では軸の範囲が異なりますが、軸のスライドは相関係数に影響がありません。片方の軸を伸縮させると影響がありますが、今回は元の問題の軸がほぼ正方形なので大きな影響はありません。いや、よく見るとちょっと長方形だったのでわずかに影響あります。この理論については以下のサイトも参照ください。

ちなみに東進ハイスクールの解答速報では以下の通り、実質的に勘だと言っています。予備校の先生が「経験を積めば分かる!」と言うのは自由だとして、公立高校の先生はそう教えて良いものでしょうか?