★★★↓一部バグがありましたので、微修正しました。新しいコードを使ってください!(2019/8/23 23:30更新)★★★
やること
前回は3次元の迷路における最短経路を求めました。今回はこれを応用して、ビネクラ杯の問題を解いてみましょう。
実行環境
WinPython3.6をおすすめしています。
必修科目
18-3の記事を必ず履修してください。これを関数化して用いますので、理解していると良いです。
import
今回使うパッケージをインポートします。グラフ中の線の色を変えるために、cm(カラーマップ)も追加しました。
import numpy as np
import matplotlib.pyplot as plt
from scipy.ndimage.filters import minimum_filter, maximum_filter
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.cm as cm問題データの読み込み
問題のページから、「generators.txt」と「equipments.txt」をダウンロードしてください。x, y, z座標がスペース区切りで4000行並んでいますので、これを読み込みます。
#============================
# 発電機データの読み込み
#============================
#ファイルを開く
file = open('generators.txt', 'r')
#読み込み
generators = []
for i in range(4000):
tmp = file.readline().split()
generators.append([int(tmp[0]), int(tmp[1]), int(tmp[2])])
#ファイルを閉じる
file.close()
#ndarray形式にする
generators = np.array(generators)
print('最初の発電機4つ:\n{}'.format(generators[:4]))
#============================
# 装置データの読み込み
#============================
#ファイルを開く
file = open('equipments.txt', 'r')
#読み込み
equipments = []
for i in range(4000):
tmp = file.readline().split()
equipments.append([int(tmp[0]), int(tmp[1]), int(tmp[2])])
#ファイルを閉じる
file.close()
#ndarray形式にする
equipments = np.array(equipments)
print('最初の装置4つ:\n{}'.format(equipments[:4]))最初の発電機4つ:
[[ 7 13 9]
[ 4 3 15]
[15 19 5]
[ 1 7 3]]
最初の装置4つ:
[[17 18 2]
[ 5 4 14]
[16 19 16]
[ 2 5 4]]generators と equipments は2次元配列です。例えば10番目の発電機のy座標は、generators[9, 1]で取り出すことができます。
ひとつのルートを見つける関数
さてここが大変です。前回のコードをできるだけそのまま関数化しました。この関数は障害物(barrier配列)、スタート座標、ゴール座標の3つを受け取って、ルートを返します。関数化にともなう主な修正点は以下です。
- コスト表示関数は削除
- 不要なもの、表示部分はコメントアウト
- 最後にrouteを返す
また、幅優先探索の後に強制終了の判定を追加しました。幅優先探索は最大999ステップ繰り返しながらコストを記入していきますが、どうしてもルートが見つからない場合はゴール地点のコストが999のままとなり、その後のルートあぶり出しの工程がエラー(というか無限に終わらない)になってしまいます。これを防ぐため、ルートが見つからなければNoneを返して終了するようにしました。
★★★↓ここにバグがありましたので、微修正しました。新しいコードを使ってください!(2019/8/23 23:30更新)★★★
#============================
# ひとつのルートを見つける関数
#============================
def find_route(barrier, start, goal):
#########################
# 前処理
#########################
#たてとよこ
#h, w, l = len(maze), len(maze[0]), len(maze[0][0])
h, w, l = len(barrier), len(barrier[0]), len(barrier[0][0])
#コスト
cost = np.zeros((h, w, l), dtype=int) + 999
#コストが書き込まれて探索が終了したマス(bool)
done = np.zeros((h, w, l), dtype=bool)
#障害物(bool)
#barrier = np.zeros((h, w, l), dtype=bool)
#プーリング用のフィルタ
g = np.array([[[0, 0, 0],
[0, 1, 0],
[0, 0, 0]],
[[0, 1, 0],
[1, 1, 1],
[0, 1, 0]],
[[0, 0, 0],
[0, 1, 0],
[0, 0, 0]]])
#mazeからスタート位置、ゴール位置、障害物位置を取得
#for i in range(h):
# for j in range(w):
# maze[i] = list(maze[i])
# for k in range(l):
# if maze[i][j][k] == 's':
# start = (i, j, k)
# cost[i, j, k] = 0
# done[i, j, k] = True
# if maze[i][j][k] == 'g':
# goal = (i, j, k)
# if maze[i][j][k] == '#':
# barrier[i, j, k] = True
cost[start[0], start[1], start[2]] = 0
done[start[0], start[1], start[2]] = True
#print('start\n{}'.format(start))
#print('goal\n{}'.format(goal))
#print('cost\n{}'.format(cost))
#print('done\n{}'.format(done))
#print('barrier\n{}'.format(barrier))
#########################
# 幅優先探索
#########################
for i in range(1, 999):
#次に進出するマスのbool
done_next = maximum_filter(done, footprint=g) * ~done
#print('done_next\n{}'.format(done_next))
#次に進出するマスのcost
cost_next = minimum_filter(cost, footprint=g) * done_next
cost_next[done_next] += 1
#print('cost_next\n{}'.format(cost_next))
#costを更新
cost[done_next] = cost_next[done_next]
#ただし障害物のコストは999とする
cost[barrier] = 999
#print('cost\n{}'.format(cost))
#探索終了マスを更新
done[done_next] = done_next[done_next]
#ただし障害物は探索終了としない
done[barrier] = False
#print('done\n{}'.format(done))
#表示
#show(i)
#終了判定
if done[goal[0], goal[1], goal[2]] == True:
break
#++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
# 【追加】 ここで一旦終了判定、ゴールのコストが999であれば、ルートが見つかっていないので強制終了
#++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
if cost[goal[0], goal[1], goal[2]] == 999:
return None
#########################
# ゴールから逆順でルート計算
#########################
point_now = goal
cost_now = cost[goal[0], goal[1], goal[2]]
route = [goal]
#print('route\n{}'.format(route))
while cost_now > 0:
#x-から来た場合
try:
if cost[point_now[0] - 1, point_now[1], point_now[2]] == cost_now - 1 and point_now[0] != 0:
#更新
point_now = (point_now[0] - 1, point_now[1], point_now[2])
cost_now = cost_now - 1
#記録
route.append(point_now)
except: pass
#x+から来た場合
try:
if cost[point_now[0] + 1, point_now[1], point_now[2]] == cost_now - 1:
#更新
point_now = (point_now[0] + 1, point_now[1], point_now[2])
cost_now = cost_now - 1
#記録
route.append(point_now)
except: pass
#y-から来た場合
try:
if cost[point_now[0], point_now[1] - 1, point_now[2]] == cost_now - 1 and point_now[1] != 0:
#更新
point_now = (point_now[0], point_now[1] - 1, point_now[2])
cost_now = cost_now - 1
#記録
route.append(point_now)
except: pass
#y+から来た場合
try:
if cost[point_now[0], point_now[1] + 1, point_now[2]] == cost_now - 1:
#更新
point_now = (point_now[0], point_now[1] + 1, point_now[2])
cost_now = cost_now - 1
#記録
route.append(point_now)
except: pass
#z-から来た場合
try:
if cost[point_now[0], point_now[1], point_now[2] - 1] == cost_now - 1 and point_now[2] != 0:
#更新
point_now = (point_now[0], point_now[1], point_now[2] - 1)
cost_now = cost_now - 1
#記録
route.append(point_now)
except: pass
#z+から来た場合
try:
if cost[point_now[0], point_now[1], point_now[2] + 1] == cost_now - 1:
#更新
point_now = (point_now[0], point_now[1], point_now[2] + 1)
cost_now = cost_now - 1
#記録
route.append(point_now)
except: pass
#ルートを逆順にする
route = route[::-1]
#print('route\n{}'.format(route))
return route「そのまま関数化しました」といっても、よほど熟達していない限り1発でうまくいくことはありません。筆者もエラーを繰り返しながら実装しました。
とりあえずNo.1をつないでみる
とりあえず、発電機(No.1)と装置(No.1)をつないでみましょう。
#============================
# メイン処理(とりあえずひとつだけつないでみる)
#============================
#通った場所(Falseで初期化)
barrier = np.zeros((20, 20, 20), dtype=bool)
#発電機と装置
print('generator[0]:\n{}'.format(generators[0]))
print('equipment[0]:\n{}'.format(equipments[0]))
#ひとつだけつないでみる
route = find_route(barrier, generators[0], equipments[0])
#ルートの表示
print('route:\n{}'.format(route))generator[0]:
[ 7 13 9]
equipment[0]:
[17 18 2]
route:
[(7, 13, 9), (8, 13, 9), (9, 13, 9), (10, 13, 9), (10, 13, 8), (11, 13, 8), (11, 13, 7), (12, 13, 7), (12, 13, 6), (12, 14, 6), (13, 14, 6), (13, 14, 5), (13, 15, 5), (14, 15, 5), (14, 15, 4), (14, 16, 4), (15, 16, 4), (15, 16, 3), (15, 17, 3), (16, 17, 3), (16, 17, 2), (16, 18, 2), array([17, 18, 2])]Noneではないので、きちんとルートが見つかりました。
No.1から順番に、できる限りつないでみる
いよいよ、発電機・装置No.1から順番につないで、どこまでスコアが伸ばせるか挑戦してみましょう。
注意点が3つあります。
まず、これからつなごうとする発電機や装置の座標にすでにケーブルが通っていたら(=barrier配列がTrueなら)処理を終了するということです。こうしないとエラー(というかやはり無限に終わらない)になってしまいます。次に、ルートが見つかったら、忘れずにそのルートを障害物(barrier配列)に反映させることです。最後に、ルートが見つからなかった場合(=Noneが返ってきた場合)も処理を終了させます。
#============================
# メイン処理(No.1から順番に、できる限りつないでみる)
#============================
#通った場所(Falseで初期化)
barrier = np.zeros((20, 20, 20), dtype=bool)
#記録用の配列
score = 0
routes = []
for i in range(4000):
print(i)
#これからつなぐスタートやゴールが、すでに障害物となっていたら終わり
if barrier[generators[i, 0], generators[i, 1], generators[i, 2]] == True:
break
if barrier[equipments[i, 0], equipments[i, 1], equipments[i, 2]] == True:
break
#ルートを見つける
route = find_route(barrier, generators[i], equipments[i])
#ルートが見つからなかったら終わり
if route is None:
break
else: #ルートが見つかったら、スコアを記録する
score += 1
routes.append(route)
#通った場所を障害物とする
for [x, y, z] in route:
barrier[x, y, z] = True
#
print('score:\n{}'.format(score))
print('routes:\n{}'.format(routes))0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
score:
17
routes:
[[(7, 13, 9), (8, 13, 9), (9, 13, 9), (10, 13, 9), (10, 13, 8), (11, 13, 8), (11, 13, 7), (12, 13, 7), (12, 13, 6), (12, 14, 6), (13, 14, 6), (13, 14, 5), (13, 15, 5), (14, 15, 5), (14, 15, 4), (14, 16, 4), (15, 16, 4), (15, 16, 3), (15, 17, 3), (16, 17, 3), (16, 17, 2), (16, 18, 2), array([17, 18, 2])], [(4, 3, 15), (4, 3, 14), (4, 4, 14), array([ 5, 4, 14])], [(15, 19, 5), (15, 19, 6), (15, 19, 7), (15, 19, 8), (15, 19, 9), (15, 19, 10), (15, 19, 11), (15, 19, 12), (15, 19, 13), (15, 19, 14), (15, 19, 15), (15, 19, 16), array([16, 19, 16])], [(1, 7, 3), (1, 6, 3), (1, 6, 4), (1, 5, 4), array([2, 5, 4])], [(8, 0, 13), (8, 0, 12), (8, 0, 11), (8, 0, 10), (8, 0, 9), (8, 0, 8), (8, 0, 7), (8, 0, 6), (8, 0, 5), (8, 0, 4), (8, 0, 3), (8, 0, 2), (7, 0, 2), (7, 0, 1), (7, 1, 1), array([6, 1, 1])], [(0, 6, 14), (1, 6, 14), (2, 6, 14), (2, 6, 13), (3, 6, 13), (3, 6, 12), (4, 6, 12), (4, 6, 11), (5, 6, 11), (5, 6, 10), (5, 5, 10), array([ 6, 5, 10])], [(14, 13, 9), (14, 14, 9), (14, 15, 9), (13, 15, 9), (13, 16, 9), (12, 16, 9), (12, 16, 8), (12, 17, 8), (11, 17, 8), (11, 17, 7), (11, 18, 7), array([10, 18, 7])], [(3, 11, 5), (3, 11, 4), (3, 12, 4), (3, 12, 3), (3, 13, 3), (3, 13, 2), (3, 14, 2), (3, 14, 1), (3, 15, 1), array([ 2, 15, 1])], [(4, 10, 19), (4, 10, 18), (4, 10, 17), (4, 10, 16), (5, 10, 16), (5, 10, 15), (6, 10, 15), (6, 10, 14), (7, 10, 14), (7, 10, 13), (8, 10, 13), (8, 10, 12), (9, 10, 12), (9, 10, 11), (10, 10, 11), (10, 10, 10), (11, 10, 10), (11, 10, 9), (12, 10, 9), (12, 10, 8), (13, 10, 8), (13, 10, 7), (14, 10, 7), (14, 10, 6), (15, 10, 6), (15, 10, 5), (16, 10, 5), (16, 10, 4), (16, 9, 4), (17, 9, 4), (17, 9, 3), (17, 8, 3), array([18, 8, 3])], [(18, 14, 12), (17, 14, 12), (16, 14, 12), (15, 14, 12), (15, 13, 12), (14, 13, 12), (14, 12, 12), (13, 12, 12), (13, 11, 12), (12, 11, 12), (12, 11, 13), (12, 10, 13), (11, 10, 13), (11, 10, 14), (11, 9, 14), (10, 9, 14), (10, 9, 15), (10, 8, 15), array([ 9, 8, 15])], [(14, 11, 8), (14, 11, 7), (14, 11, 6), (14, 12, 6), (13, 12, 6), (13, 12, 5), (13, 13, 5), (12, 13, 5), (12, 14, 5), (11, 14, 5), (11, 14, 4), (11, 15, 4), (10, 15, 4), (10, 15, 3), (10, 16, 3), (9, 16, 3), (9, 16, 2), (9, 17, 2), array([ 8, 17, 2])], [(11, 17, 9), (11, 16, 9), (11, 15, 9), (11, 14, 9), (11, 13, 9), (11, 12, 9), (10, 12, 9), (10, 11, 9), (9, 11, 9), (9, 10, 9), (8, 10, 9), (8, 9, 9), (7, 9, 9), (7, 8, 9), (6, 8, 9), (6, 7, 9), (5, 7, 9), (5, 6, 9), (4, 6, 9), (4, 6, 10), (4, 5, 10), (3, 5, 10), (3, 5, 11), (3, 4, 11), (2, 4, 11), (2, 4, 12), (2, 3, 12), (1, 3, 12), (1, 3, 13), (1, 2, 13), array([ 0, 2, 13])], [(15, 16, 14), (15, 15, 14), (14, 15, 14), (14, 14, 14), (13, 14, 14), (13, 13, 14), (12, 13, 14), (12, 12, 14), (11, 12, 14), (11, 11, 14), (10, 11, 14), (10, 11, 13), (10, 10, 13), (10, 10, 12), (10, 9, 12), (9, 9, 12), (9, 9, 11), (9, 8, 11), (8, 8, 11), (8, 8, 10), (8, 7, 10), (7, 7, 10), (7, 7, 9), (7, 6, 9), (6, 6, 9), (6, 6, 8), (6, 5, 8), (5, 5, 8), (5, 5, 7), (5, 4, 7), (4, 4, 7), (4, 4, 6), (4, 3, 6), array([3, 3, 6])], [(13, 9, 7), (13, 9, 8), (13, 9, 9), (13, 9, 10), (13, 9, 11), (13, 9, 12), (13, 9, 13), (13, 9, 14), (13, 9, 15), (13, 9, 16), (13, 8, 16), (13, 8, 17), (13, 7, 17), (13, 7, 18), (13, 6, 18), array([12, 6, 18])], [(15, 15, 3), (15, 14, 3), (15, 14, 4), (15, 13, 4), (15, 13, 5), (15, 12, 5), (15, 12, 6), (15, 11, 6), (15, 11, 7), (15, 10, 7), (15, 9, 7), (14, 9, 7), (14, 9, 8), (14, 8, 8), (13, 8, 8), (13, 8, 9), (13, 7, 9), (12, 7, 9), (12, 7, 10), (12, 6, 10), array([11, 6, 10])], [(5, 12, 10), (6, 12, 10), (6, 13, 10), (7, 13, 10), (7, 14, 10), (8, 14, 10), (8, 14, 9), (9, 14, 9), (9, 14, 8), (9, 15, 8), (10, 15, 8), (10, 15, 7), (10, 16, 7), array([11, 16, 7])], [(11, 9, 7), (11, 10, 7), (11, 10, 8), (11, 11, 8), (11, 11, 9), (11, 11, 10), (10, 11, 10), (10, 11, 11), (9, 11, 11), (9, 11, 12), (8, 11, 12), (8, 11, 13), (7, 11, 13), (7, 11, 14), (6, 11, 14), (6, 11, 15), (6, 12, 15), array([ 5, 12, 15])]]i=17でルートが見つからなかったのか、処理が終了しました。つまり、i=0~16までの17システムがつながったということです。
見つかったすべてのルートを可視化する
人間は何事も可視化しないと理解できない生物ですので、見つかったすべてのルート(routes)を図にしてみましょう。
#########################
# 表示関数
#########################
def show_routes(routes):
#
fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(111, projection='3d')
#線を表示
for n in range(len(routes)):
route = routes[n]
for i in range(1, len(route)):
ax.plot([route[i - 1][0], route[i][0]], [route[i - 1][1], route[i][1]], [route[i - 1][2], route[i][2]], c=cm.jet(n/len(routes)), linewidth=5)
#
ax.auto_scale_xyz([0, 20], [0, 20], [0, 20])
ax.set_xlabel('x'); ax.set_ylabel('y'); ax.set_zlabel('z')
plt.show(); plt.close()
show_routes(routes)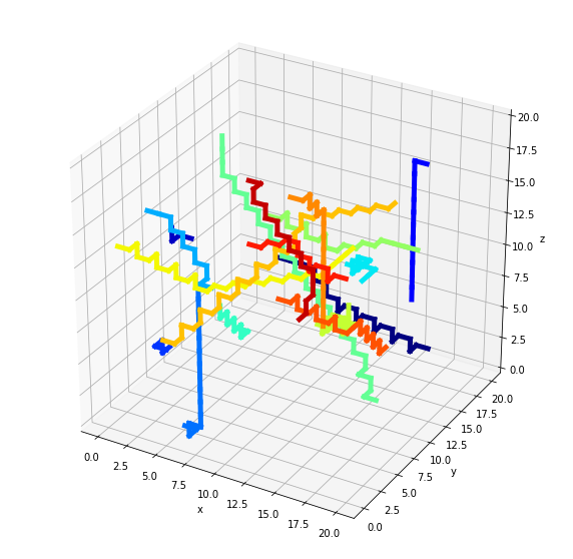
どれが何番目のルートかはわかりませんが、おそらく17本の線が表示されています!
結果の保存
指定された形式で結果を出力します。
#########################
# 結果の保存
#########################
with open('yourname.txt', mode='w') as f:
f.write('{}\n'.format(score))
for route in routes:
f.write('{}\n'.format(len(route)))
for [x, y, z] in route:
f.write('{} {} {}\n'.format(x, y, z))このようなファイルになりました。これを提出すれば、スコア17が獲得できます!(え)
まとめ
ここまで長かったですが、ようやくビネクラ杯の問題を解くことができました。スコアはたった17ですが、少し工夫することでさらに高いスコアが出る可能性があります。ぜひ、さらなる高みを目指してください!