やること
これまで、量子アニーリングでパズルを解いたり巡回セールスマン問題を解いたりしました。
今回は構造最適化(トポロジー最適化)を試してみましょう。トポロジー最適化(Topology Optimization)は力学に基づいて構造物の最適な形状を求める方法論です。こんな感じの肉抜き構造を見たことあるのではないでしょうか。
本来はきちんと応力を計算するものですが、ここでは簡易的に形状だけに着目してQUBOを立ててみます。
実行環境
WinPython3.6をおすすめしています。
Google Colaboratoryが利用可能です。

構造物の作成
鉄板状の構造物を仮定します。
import numpy as np
import matplotlib.pyplot as plt
from pyqubo import Binary
from dwave_qbsolv import QBSolv
#可視化の関数
def show(dist):
plt.imshow(dist)
plt.colorbar()
plt.show()
#フィールドサイズ
w, h = 9, 15
#縁の配列
edge = np.zeros((h, w), int)
#基本
edge[:, 0] = 1
edge[:, -1] = 1
edge[0, :] = 1
edge[-1, :] = 1
#内部
edge[7, :3] = 1
edge[7, -2:] = 1
print(edge)
show(1 - edge)[[1 1 1 1 1 1 1 1 1]
[1 0 0 0 0 0 0 0 1]
[1 0 0 0 0 0 0 0 1]
[1 0 0 0 0 0 0 0 1]
[1 0 0 0 0 0 0 0 1]
[1 0 0 0 0 0 0 0 1]
[1 0 0 0 0 0 0 0 1]
[1 1 1 0 0 0 0 1 1]
[1 0 0 0 0 0 0 0 1]
[1 0 0 0 0 0 0 0 1]
[1 0 0 0 0 0 0 0 1]
[1 0 0 0 0 0 0 0 1]
[1 0 0 0 0 0 0 0 1]
[1 0 0 0 0 0 0 0 1]
[1 1 1 1 1 1 1 1 1]]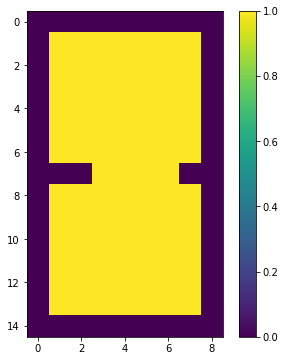
黄色い部分が構造物です。くびれが入った形状です。
縁からの距離を計算
縁からの距離を計算します。縁に1が並んでいるedge配列を利用して、最も近い1からの距離をdist配列に書き込みます。
#縁からの距離配列
dist = np.zeros((h, w), float)
#縁からの距離を計算
i_ones = np.where(edge == 1)[0]
j_ones = np.where(edge == 1)[1]
for i in range(h):
for j in range(w):
tmp = ((i_ones - i)**2 + (j_ones - j)**2)**0.5
dist[i, j] = np.min(tmp)
print(dist)
show(dist)[[0. 0. 0. 0. 0. 0. 0. 0. 0. ]
[0. 1. 1. 1. 1. 1. 1. 1. 0. ]
[0. 1. 2. 2. 2. 2. 2. 1. 0. ]
[0. 1. 2. 3. 3. 3. 2. 1. 0. ]
[0. 1. 2. 3. 3.61 3. 2. 1. 0. ]
[0. 1. 2. 2.24 2.83 2.83 2. 1. 0. ]
[0. 1. 1. 1.41 2.24 2.24 1.41 1. 0. ]
[0. 0. 0. 1. 2. 2. 1. 0. 0. ]
[0. 1. 1. 1.41 2.24 2.24 1.41 1. 0. ]
[0. 1. 2. 2.24 2.83 2.83 2. 1. 0. ]
[0. 1. 2. 3. 3.61 3. 2. 1. 0. ]
[0. 1. 2. 3. 3. 3. 2. 1. 0. ]
[0. 1. 2. 2. 2. 2. 2. 1. 0. ]
[0. 1. 1. 1. 1. 1. 1. 1. 0. ]
[0. 0. 0. 0. 0. 0. 0. 0. 0. ]]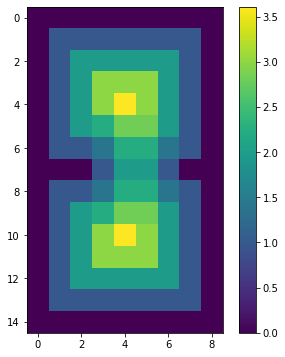
これから、縁から遠い部分に穴を開けます。丸い穴が2つ開くのか、細長い穴が1つ開くのか、それが焦点になります。
量子ビットの用意
量子ビットを135個用意します。また、これらを二次元配列に配したときのインデックス配列も用意しておきます。
#量子ビットを定義
for i in range(h*w):
command = 'q{:03} = Binary(\'q{:03}\')'.format(i, i)
print(command)
exec(command)
#量子ビットインデックス
idx = np.arange(h*w).reshape(h, w)
print(idx)q000 = Binary('q000')
q001 = Binary('q001')
・・・
q133 = Binary('q133')
q134 = Binary('q134')
[[ 0 1 2 3 4 5 6 7 8]
[ 9 10 11 12 13 14 15 16 17]
[ 18 19 20 21 22 23 24 25 26]
[ 27 28 29 30 31 32 33 34 35]
[ 36 37 38 39 40 41 42 43 44]
[ 45 46 47 48 49 50 51 52 53]
[ 54 55 56 57 58 59 60 61 62]
[ 63 64 65 66 67 68 69 70 71]
[ 72 73 74 75 76 77 78 79 80]
[ 81 82 83 84 85 86 87 88 89]
[ 90 91 92 93 94 95 96 97 98]
[ 99 100 101 102 103 104 105 106 107]
[108 109 110 111 112 113 114 115 116]
[117 118 119 120 121 122 123 124 125]
[126 127 128 129 130 131 132 133 134]]条件1:全体から22個の量子ビットを抜く
条件1として、全体から22個の量子ビットを抜くことにします。0は残す、1は抜く場所として、これまで頻繁に使用してきた「n個の量子ビットからm個を1にする」の方法を使って「135個の量子ビットから22個を1にする」とします。
#全体から2個の量子ビットを抜く
H = 0
command = '(' + ' + '.join(['q{:03}'.format(i) for i in range(h*w)]) + ' - {})**2'.format(22)
print(command)
H += eval(command)(q000 + q001 + q002 + q003 + q004 + q005 + q006 + q007 + q008 + q009 + q010 + q011 + q012 + q013 + q014 + q015 + q016 + q017 + q018 + q019 + q020 + q021 + q022 + q023 + q024 + q025 + q026 + q027 + q028 + q029 + q030 + q031 + q032 + q033 + q034 + q035 + q036 + q037 + q038 + q039 + q040 + q041 + q042 + q043 + q044 + q045 + q046 + q047 + q048 + q049 + q050 + q051 + q052 + q053 + q054 + q055 + q056 + q057 + q058 + q059 + q060 + q061 + q062 + q063 + q064 + q065 + q066 + q067 + q068 + q069 + q070 + q071 + q072 + q073 + q074 + q075 + q076 + q077 + q078 + q079 + q080 + q081 + q082 + q083 + q084 + q085 + q086 + q087 + q088 + q089 + q090 + q091 + q092 + q093 + q094 + q095 + q096 + q097 + q098 + q099 + q100 + q101 + q102 + q103 + q104 + q105 + q106 + q107 + q108 + q109 + q110 + q111 + q112 + q113 + q114 + q115 + q116 + q117 + q118 + q119 + q120 + q121 + q122 + q123 + q124 + q125 + q126 + q127 + q128 + q129 + q130 + q131 + q132 + q133 + q134 - 22)**2長い式ですが、一番後ろでちゃんと-22してから2乗しています。
条件2:縁から遠いビットほど抜かれやすい
条件2として、縁から遠いビットほど抜かれやすくします。各量子ビットが1になった場合に、縁からの距離に比例した報酬(負のコスト)を発生させます。縁からの距離に-0.1をかけた値にします。
#縁から遠いビットほど抜かれやすい
for i in range(h):
for j in range(w):
reward = -0.1 * dist[i, j]
command = '({} * q{:03})'.format(reward, idx[i, j])
print(command)
H += eval(command)・・・
(-0.2 * q092)
(-0.3 * q093)
(-0.361 * q094)
(-0.3 * q095)
(-0.2 * q096)
・・・縁から一番遠いビットは距離3.61なので、もしこのビットが1になって抜けたら-0.361のコスト(0.361の報酬)が発生することになります。
条件3:隣接する量子ビットは一緒に抜かれやすい
条件3として、隣接する量子ビットは一緒に抜かれやすくします。こうすることで、小さな穴がたくさん抜けるのではなく、ある程度の大きさの穴がボンと開くことを期待します。巡回セールスマン問題でも使用した「量子ビットaと量子ビットbが同時に1になったらペナルティを与える」を使って、隣接するビットが同時に抜かれた場合に0.01の報酬(-0.01のコスト)を発生させます。
#隣接する量子ビットは一緒に抜かれやすい
reward = -0.01
for i in range(h):
for j in range(w):
if i < h - 1:
command = '({} * q{:03} * q{:03})'.format(reward, idx[i, j], idx[i+1, j])
print(command)
H += eval(command)
if j < w - 1:
command = '({} * q{:03} * q{:03})'.format(reward, idx[i, j], idx[i, j+1])
print(command)
H += eval(command)(-0.01 * q000 * q009)
(-0.01 * q000 * q001)
・・・
(-0.01 * q132 * q133)
(-0.01 * q133 * q134)246行くらい、ひたすら同じコストが定義されました。
アニーリング
量子ビットが多いので問題を分割してサンプリングするQBSolv()を使います。以前に大規模な問題を解くときに使用した方法です。
#コンパイル
model = H.compile()
qubo, offset = model.to_qubo()
#print('qubo\n{}'.format(qubo))
#問題を分割してサンプリングしまくる
response = QBSolv().sample_qubo(qubo, num_repeats=1000)
#レスポンスの確認
print('response')
for (sample, energy, occurrence) in response.data():
print('Sample:{} Energy:{} Occurrence:{}'.format(list(sample.values()), energy, occurrence))
tmp = np.array(list(sample.values())).reshape(h, w)
print(tmp)
show(1 - (edge + tmp))response
Sample:[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] Energy:-490.49799999999993 Occurrence:51
[[0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0]
[0 0 0 1 1 1 0 0 0]
[0 0 0 1 1 1 0 0 0]
[0 0 0 1 1 1 0 0 0]
[0 0 0 0 1 1 0 0 0]
[0 0 0 0 0 0 0 0 0]
[0 0 0 0 1 1 0 0 0]
[0 0 0 1 1 1 0 0 0]
[0 0 0 1 1 1 0 0 0]
[0 0 0 1 1 1 0 0 0]
[0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0]]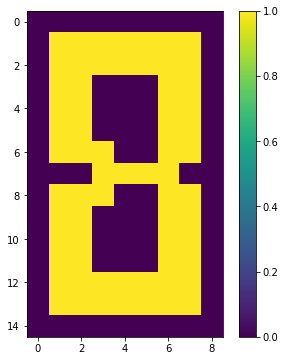
エネルギー-490.49で、2つの穴が開く解が得られました。
コストを変えると?
次に、「隣接する量子ビットは一緒に抜かれやすい」のコストを-0.01から-0.05に増やしてみます。隣接するビットが一緒に抜かれた場合の報酬を増やすということは、よりまとまって抜かれやすくなるということです。
response
Sample:[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] Energy:-491.7 Occurrence:42
[[0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0]
[0 0 0 1 1 1 0 0 0]
[0 0 0 1 1 1 0 0 0]
[0 0 0 0 1 1 0 0 0]
[0 0 0 0 1 1 0 0 0]
[0 0 0 0 1 1 0 0 0]
[0 0 0 0 1 1 0 0 0]
[0 0 0 0 1 1 0 0 0]
[0 0 0 1 1 1 0 0 0]
[0 0 0 1 1 1 0 0 0]
[0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0]]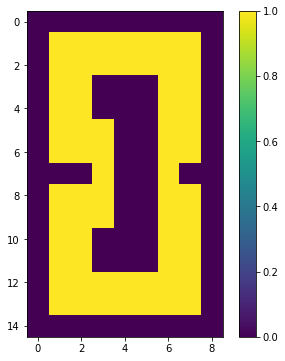
今度は大きな穴が1つ開きました。
おわりに
応力の計算なんかは一切していないのでエセです。
ちなみに分割サンプリングの方法だとD-wave Leapの月間1分を消費しないようですね(本当?)。サンプリングも高速で正確に感じるので、検証ではこれを使っておけば良いような気がします。

