やること
2023/5/20追記:応用A4を追加
2023/5/23追記:応用Dを追加
量子アニーリングで設定可能な条件式(QUBOで表現可能な条件)をまとめました。何度も参照するので私はブックマークしています。基本の条件設定から、図のように派生していきます。
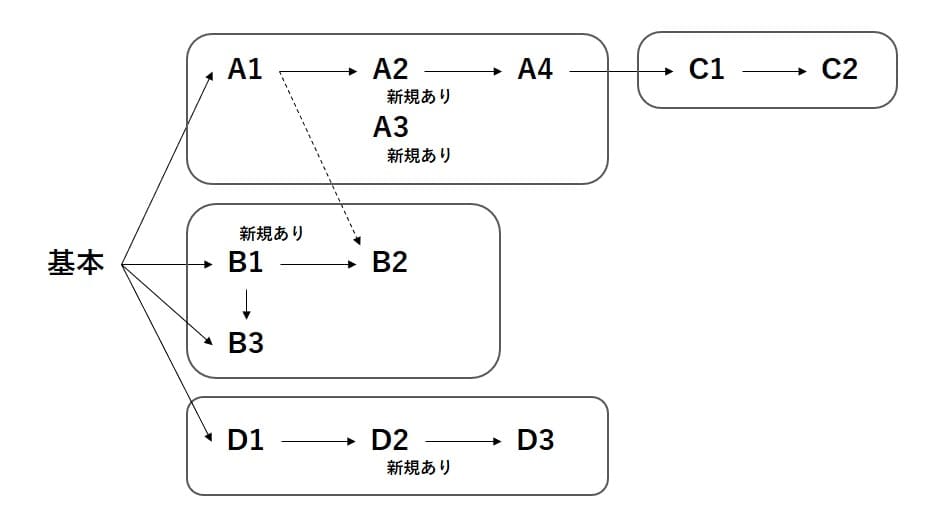
重みの係数として「k」を使っていますが、これは1とか0.1に設定します。絶対守ってほしい条件設定では1とし、コスト(ペナルティ)のように守られないものもある場合は0.1などオーダーを落とします。もう一段階落としたければ0.01といったように。
q0, q1・・・は量子ビットを表しています。これが0になるか1になるかを考えているわけですが、実際に式に0や1を代入してみて、達成したい条件においてエネルギーが最小になることを確認してください(そうなっているはずです)。逆に、達成したい条件から一つでもひっくり返るとエネルギーが高くなるはずです。
注意点として、ここに掲載した式以外にも表現方法があるものもあります。この記事では「基本」を一つ定め、そこから派生する形で整理しました。
基本
基本「n個の量子ビットからm個を1にする」
3個の量子ビットから2個を1にする(=3個の量子ビットの合計を2にする)
H += k * (q0 + q1 + q2 - 2)**21個の量子ビットを0にする
#「1個の量子ビットから0個を1にする」と同じ
H += k * (q0 - 0)**22個の量子ビットを0、1逆にする
#「2個の量子ビットから1個を1にする」と同じ
H += k * (q0 + q1 - 1)**2応用A
A1「n個の量子ビットからm個またはm+1個を1にする」
3個の量子ビットから1個または2個を1にする
#(基本を利用)「3個の量子ビットから1.5個を1にする」と考える
H += k * (q0 + q1 + q2 - 1.5)**23個の量子ビットの和を1以下にする
#「3個の量子ビットから0個または1個を1にする」と同じ
H += k * (q0 + q1 + q2 - 0.5)**2※「m個またはm+2個を1にする」や「m個またはm+3個を1にする」は応用D2へ
A2「2個の量子ビットが同時に1になったらペナルティを与える」
2個の量子ビットが同時に1になったらペナルティを与える
#(新しい表現)2個の量子ビットが同時に1になったときのみペナルティが有効になると考える
H += k * (q0 * q1)#(A1を利用)「2個の量子ビットから0個または1個を1にする」と同じ
H += k * (q0 + q1 - 0.5)**2A3「2個の量子ビットが同時に1になったら報酬を与える」
2個の量子ビットが同時に1になったら報酬を与える
#(新しい表現)2個の量子ビットが同時に1になったときのみ報酬が有効になると考える
H += -k * (q0 * q1)#(A1を利用)「2個の量子ビットから0個または1個を1にする」から遠くすると考える
H += -k * (q0 + q1 - 0.5)**2A4「2個の量子ビットが同時に0になったらペナルティ(報酬)を与える」
2個の量子ビットが同時に0になったらペナルティを与える。上記A2, A3において q0 を (1 – q0) に置き換えれば0と1の意味がひっくり返り「0のときだけペナルティ(報酬)が有効になる」を表現できる。
#(A2, A3を利用)"q0"を"(1 - q0)"に置き換えれば0と1の意味がひっくり返る
H += k * (1 - q0) * (1 - q1)応用B
B1「2個の量子ビットを揃える」
2個の量子ビットを同じ値(0または1)に揃える
#新しい表現
H += k * (q0 - q1)**2#(基本を利用)「2個の量子ビットから1個を1にする」から遠くすると考える
H += -k * (q0 + q1 - 1)**2B2「すべての量子ビットを揃える」
3個の量子ビットを同じ値(0または1)に揃える
#(A1を利用)「3個の量子ビットから1.5個を1にする」から遠くすると考える
H += -k * (q0 + q1 + q2 - 1.5)**2#(B1を利用)「2個の量子ビットを揃える」を連鎖させる
H += k * (q0 - q1)**2
H += k * (q1 - q2)**2B3「すべての量子ビットを0、1交互にする」
3個の量子ビットを0、1交互にする
#(基本を利用)「2個の量子ビットから1個を1にする」を連鎖させる
H += k * (q0 + q1 - 1)**2
H += k * (q1 + q2 - 1)**2#(B1を利用)「2個の量子ビットを揃える」の逆を連鎖させる
H += -k * (q0 - q1)**2
H += -k * (q1 - q2)**2応用C
C1「2個の量子ビットを降順にする」
q0 ≧ q1 にする(=[0, 1] になったらペナルティを与える)
#(A4を利用)2個の量子ビットが[0, 1]になったときのみペナルティが有効になると考える
H += k * (1 - q0) * q1C2「すべての量子ビットを降順にする」
q0 ≧ q1 ≧ q2 にする
#(C1を利用)「2個の量子ビットを降順にする」を連鎖させる
H += k * (1 - q0) * q1
H += k * (1 - q1) * q2応用D
D1 解が0と1だけの方程式
「1x + 2y + 3z = 3」を満たす変数 [x, y, z](ただし0または1のみ)の組は?
#(基本を利用)量子ビットが1になった項だけ重みが有効になり、その合計が3
H = (1*q0 + 2*q1 + 3*q2 - 3)**2Sample:[0, 0, 1]
Sample:[1, 1, 0][x, y, z] = [0, 0, 1] or [1, 1, 0]
補足:これは「重さ1, 2, 3のボールのどれを取れば合計3の重さになるか?」を解くことに相当している。量子ビットが1になったボールは取る、0になったボールは取らない。取ったボールの合計が3になる。
D2 解が0と1だけの方程式(右辺が複数)
「1x + 2y + 3z = 1 or 3」を満たす変数 [x, y, z](ただし0または1のみ)の組は?(D1の発展形、補助ビットで右辺を表現する)
#量子ビットを用意する(変数の個数だけ)
q0 = Binary('q0')
q1 = Binary('q1')
q2 = Binary('q2')
#補助ビットを用意する(右辺のパターン数だけ)
s0 = Binary('s0')
s1 = Binary('s1')
#補助ビットは1個を1にする、よって(1*s0 + 3*s1)は1または3になる
H = 0
H += (s0 + s1 - 1)**2
#量子ビットが1になった項だけ重みが有効になり、その合計が1または3
H += (1*q0 + 2*q1 + 3*q2 - (1*s0 + 3*s1))**2Sample:[0, 0, 1, 0, 1] #後ろ2つは補助ビット
Sample:[1, 1, 0, 0, 1]
Sample:[1, 0, 0, 1, 0][x, y, z] = [0, 0, 1], [1, 1, 0], [1, 0, 0]
D3 解が0と1だけの不等式
「1x + 2y + 3z ≦ 3」を満たす変数 [x, y, z](ただし0または1のみ)の組は?(D2の発展形)
#量子ビットを用意する(変数の個数だけ)
q0 = Binary('q0')
q1 = Binary('q1')
q2 = Binary('q2')
#補助ビットを用意する(右辺のパターン数だけ)
s0 = Binary('s0')
s1 = Binary('s1')
s2 = Binary('s2')
s3 = Binary('s3')
#補助ビットは1つだけ1にする、よって(0*s0 + 1*s1 + 2*s2 + 3*s3)は0, 1, 2, 3のどれかになる
H = 0
H += (s0 + s1 + s2 + s3 - 1)**2
#量子ビットが1になった項だけ重みが有効になり、その合計が0, 1, 2, 3のどれか
H += (1*q0 + 2*q1 + 3*q2 - (0*s0 + 1*s1 + 2*s2 + 3*s3))**2Sample:[0, 0, 1, 0, 0, 0, 1] #後ろ4つは補助ビット
Sample:[1, 1, 0, 0, 0, 0, 1]
Sample:[1, 0, 0, 0, 1, 0, 0]
Sample:[0, 1, 0, 0, 0, 1, 0]
Sample:[0, 0, 0, 1, 0, 0, 0][x, y, z] = [0, 0, 1], [1, 1, 0], [1, 0, 0], [0, 1, 0], [0, 0, 0]
その他:One-hotエンコーディング
「1~nの自然数のどれかになる」
1~3の自然数のどれかにする(=3個の量子ビットから1個を1にする。1になった場所を自然数に割り当てる)
#(基本を利用)「n個の量子ビットから1個を1にする」を利用したOne-hotエンコーディング
H += k * (q0 + q1 + q2 - 1)**2その他:N-bitエンコーディング
「0~255の整数とする」
xを0~255の整数とする(量子ビットx0~x7を使用)
# x0~x7は量子ビット(0≦x<256)
x = 128*x0 + 64*x1 + 32*x2 + 16*x3 + 8*x4 + 4*x5 + 2*x6 + x7「10~20の小数とする」
aを10~20の小数とする(量子ビットa0~a7を使用)(8bitなので256段階の刻み)
# a0~a7は量子ビット(10≦a<20)
a = 10 + 10 * ((128*a0 + 64*a1 + 32*a2 + 16*a3 + 8*a4 + 4*a5 + 2*a6 + a7) / 256)その他:アニーリング基本形
量子ビットは q[0] のように配列で定義する流派もありますが、私は q0 や q001 のように個別の変数として定義する派です。使いやすい方で良いと思います。
サンプリングにもいろいろなパッケージがありますが、dwave_qbsolv.QBSolv() は無料、オフライン、そこそこの量子ビット数にも対応できるので愛用しています。もちろん疑似アニーリングではありますが。
2023年6月追記:QUBOアニーリングの「TYTAN」が登場。便利な関数がいくつも用意されていて簡単に書けるのでおすすめ。個人利用、商用利用ともに無料。
「TYTAN」の使い方、ドキュメント↓
チュートリアルコース↓
最小コード↓
from tytan import *
#量子ビットを用意
x = symbols('x')
y = symbols('y')
z = symbols('z')
#式を記述(3個のうち2個だけ1にする)
H = (x + y + z - 2)**2
#コンパイル
qubo, offset = Compile(H).get_qubo()
print(f'offset\n{offset}')
#サンプラー選択
solver = sampler.SASampler()
#サンプリング
result = solver.run(qubo)
#結果
for r in result:
print(r)