やること
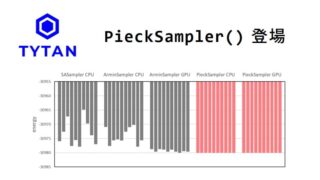
先日、QUBOアニーリングパッケージ「TYTAN」に対ワンホット高速GPUサンプラー「PieckSampler」が試験導入されました。(初めての人が見たら何言ってるか分からない文章)
本当に使えるかどうか、1000量子ビット規模の配送計画問題を解いてみたいと思います。
TYTANについて
「TYTAN」はOSSのアニーリングSDKです。
チュートリアル教材はこちら。また、毎週木曜日22時にオンライン勉強会もやっています(2024年2月現在)。
discordコミュニティもあるので気軽に質問できます。
配送計画問題の作成
100m×100mのフィールドに4人のサンタと10人の子どもをランダムに配置します。サンタはプレゼントを一つずつ持ってプレゼントを配りに行きます。2人以上に配る場合は一々拠点に戻ってプレゼントを補給する必要があります。すべての子どもに1個ずつプレゼントが行き渡り、すべてのサンタが帰宅するまでの時間が最小になる配送計画を求めます。
まずは数を定義し、問題の固定のために乱数シードも指定します。
from tytan import *
import numpy as np
import numpy.random as nr
import matplotlib.pyplot as plt
#サンタの数
N = 4
#子どもの数
M = 10
#乱数シード
nr.seed(2)サンタと子どもの座標を生成します。
def show():
plt.figure()
#サンタ拠点
plt.plot(santa[:, 0], santa[:, 1], 'ok', markerfacecolor='w', markersize=20)
#サンタ本体
for i in range(N):
plt.text(santa[i, 0], santa[i, 1], f'{i}', ha='center', va='center')
#子ども本体
for i in range(M):
plt.text(kids[i, 0], kids[i, 1], f'{i}', ha='center', va='center', c='r')
plt.xlabel('x'); plt.ylabel('y')
plt.xlim(0, 100); plt.ylim(0, 100)
plt.show(); print()
#サンタ座標
santa = nr.randint(0, 100, (N, 2))
print(santa)
#子ども座標
kids = nr.randint(0, 100, (M, 2))
print(kids)
#確認
show()[[40 15]
[72 22]
[43 82]
[75 7]]
[[34 49]
[95 75]
[85 47]
[63 31]
[90 20]
[37 39]
[67 4]
[42 51]
[38 33]
[58 67]]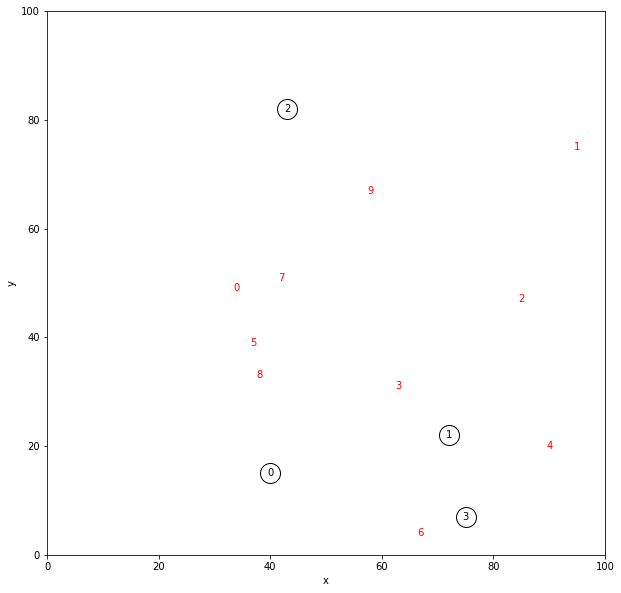
白丸がサンタの拠点、黒字がサンタ、赤字が子どもです。座標は分かりやすく整数にしました。
距離行列の計算
各サンタから各子どもへの距離行列を用意します。こちらも分かりやすく整数にしています。
#距離マトリックス(サンタ→子ども)
dist = np.zeros((N, M))
for i in range(N):
for j in range(M):
dist[i, j] = np.linalg.norm(santa[i] - kids[j])
dist = dist.astype(int)
print(dist)[[34 81 55 28 50 24 29 36 18 55]
[46 57 28 12 18 38 18 41 35 47]
[34 52 54 54 77 43 81 31 49 21]
[58 70 41 26 19 49 8 55 45 62]]貪欲法の解
比較用にシンプルな貪欲法で解を求めてみました。各サンタが担当する子どもIDです。
[[8, 5],
[3, 2, 1],
[9, 7],
[6, 4, 0]]1ステップあたり1m進むとして、194ステップで完了となりました。
QUBO定式化
サンタ数×子ども数の量子ビットを用意してワンホット制約を設定します。
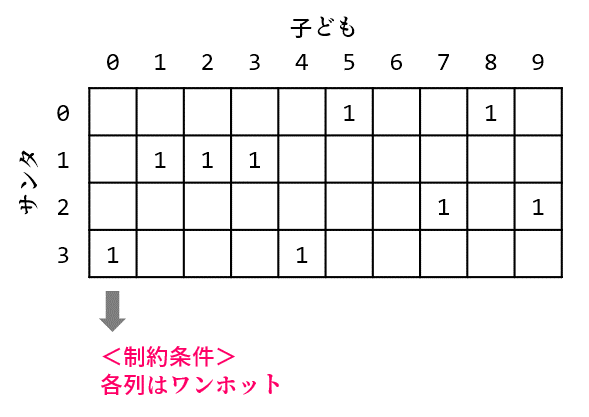
あるサンタの「量子ビット列」と「子どもへの距離列」の内積がそのサンタの移動距離です。(往復なので本当は2倍するべきですが、意味は変わらないので省略します)
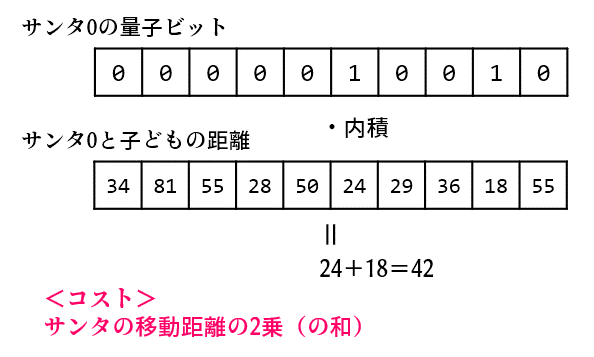
各サンタの移動距離の2乗の合計をコストにして、これが最小になる状態を探索します。
#量子ビットを用意
q = symbols_list([N, M], 'q{}_{}')
#制約条件(各子どもは1人のサンタに訪問される)
Hconst = 0
for j in range(M):
Hconst += (sum(q[:, j]) - 1)**2
#コスト(各サンタの移動距離の2乗の合計)
Hcost = 0
for i in range(N):
Hcost += sum(q[i, :] * dist[i, :])**2
#合体
H = 1000*Hconst + HcostPieckSampler() でサンプリングします。サンプリング数20000、イテレーションはデフォルトの2000にしました。
#コンパイル
qubo, offset = PieckCompile(H).get_qubo()
print(f'offset={offset}')
#サンプラー選択
solver = sampler.PieckSampler(seed=None)
#サンプリング
result = solver.run(qubo, shots=20000, T_num=2000)
#確認
for r in result[:1]:
print(f'Energy {r[1]}, Occurrence {r[2]}')
#さくっと配列に
arr, subs = Auto_array(r[0]).get_ndarray('q{}_{}')
#ワンホット確認
print(arr)
print(np.sum(arr, axis=0))
print(np.sum(arr, axis=1))------ PieckCompile ------
Extracted onehot group: 10
Extracted onehot keys: 40
--------------------------
offset=10000.0
------ PieckSampler ------
MODE: GPU
DEVICE: cuda:0
--------------------------
Energy 7865.0, Occurrence 12506
[[1 0 0 0 0 1 0 0 1 0]
[0 1 0 1 0 0 0 0 0 0]
[0 0 0 0 0 0 0 1 0 1]
[0 0 1 0 1 0 1 0 0 0]]
[1 1 1 1 1 1 1 1 1 1]
[3 2 2 3]コンパイルのログを見ると10組(40量子ビット)のワンホット制約が検出されて何か対策が行われたようです。サンプリングは4秒かかりました。解がワンホット制約を満たしていることも確認できました。
各サンタが担当する子どもIDに戻して可視化します。
#各サンタが担当するこどもID
ans = []
for i in range(N):
ans.append(list(np.where(arr[i, :]==1)[0]))
print(ans)[[0, 5, 8],
[1, 3],
[7, 9],
[2, 4, 6]]152ステップで完了しました!(貪欲法では194ステップ)
問題の規模を大きくする
サンタ数と子ども数を増やして1000量子ビット規模にします。
#サンタの数
N = 20
#子どもの数
M = 50
#乱数シード
nr.seed(2)貪欲法だと一瞬で解が求まりますが、186ステップかかります。
PieckSampler() はサンプリング数20000は変えず、イテレーション数12000に上げて3分弱かかりました。
#サンプリング
result = solver.run(qubo, shots=20000, T_num=12000)------ PieckCompile ------
Extracted onehot group: 50
Extracted onehot keys: 1000
--------------------------
offset=50000.0
------ PieckSampler ------
MODE: GPU
DEVICE: cuda:0
--------------------------
Energy -21492.0, Occurrence 1
(arr省略)
[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1]
[3 3 2 0 2 4 1 2 2 2 3 4 4 3 2 3 3 2 2 3]一人サボってるサンタがいるような気もしますが、序盤から左側のサンタ過疎地域を積極的に攻略しているのが確認できます。貪欲法は186ステップ、QUBOアニーリングは118ステップと圧倒的に良い解が得られました。なお計算時間()
参考
参考までに、通常の高速GPU「ArminSampler」でも一応解が出ました。(制約条件の重みを調整してパワーも上げています)
#コンパイル
qubo, offset = Compile(H).get_qubo()
print(f'offset={offset}')
#サンプラー選択
solver = sampler.ArminSampler(seed=None)
#サンプリング
result = solver.run(qubo, shots=50000, T_num=12000, show=True)offset=5000000.0
MODE: GPU
DEVICE: cuda:0
Energy -4731342.0, Occurrence 1
(arr省略)
[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1]
[0 2 5 1 4 5 2 5 7 8 0 1 0 0 0 1 1 2 4 2]ただ、ワンホットを満たすことにかなりリソースを取られてしまい、「とりあえず出しましたよ」って感じの品質になってしまいました。ご覧ください。
おわりに
QUBOは楽しいのですが、0と1だけで表現するという強烈な制限のためにワンホットという無理が生じてしまうのですよね。そしてそれを解決するための特殊なサンプラーを開発・・・果たして正しい道なのでしょうか。
「おい、お前QUBOやるときは得意のGAを引き合いに出さないよな?怪しいぞ!」
(;^_^A
追記:Youtubeに比較動画アップしました