やること
HOBO対応の疑似アニーリングパッケージ「HOBOTAN」が登場しました。
これまでQUBOアニーリングパッケージ「TYTAN」の開発手伝いをしてきまして、教材もいくつか公開してきました。TYTANはGPU対応もされ、超並列サンプリングが可能になっています。
QUBO(Quadratic Unconstrained Binary Optimization)は2つの量子ビットの相互作用までを許容した「2次の制約」の下に定式化を行います。3次以上の項は使用できません(*)。様々な組合せ最適化問題をいかに2次以下の式に変換するかがポイントでした。
(*)次数下げのテクニックがあるようですが、必要な量子ビット数が膨大になるため現実的ではないそうです。
一方、3次以上の制約を許容したモデルはHOBO(Higher Order Binary Optimization)と呼ばれます。例えば「3つの量子ビットが同時に1になってはいけない」といった制約条件が設定できるようになります。
HOBO対応の疑似アニーリングパッケージが存在しないらしいので、2024年7月26日に有志による開発チームが発足し、2024年7月26日にテスト版のパッケージ「HOBOTAN」が公開されました。
翌日にはGPU対応され、高次制約問題の超並列サンプリングが実現しました(は?)。本当に使えるかどうか、サンプル問題を解いてみたいと思います。
TYTANについて
前身となる「TYTAN」はOSSのアニーリングSDKです。
チュートリアル教材はこちら。また、毎週木曜日22時にオンライン勉強会もやっています(2024年7月現在)。
私のオンライン講義でよければこちらから見れます。(教材は上記リンクの中の「第3世代基礎コース」にあります)
discordコミュニティもあるので気軽に質問できます。
HOBOTANについて
それを元にしてできたのが「HOBOTAN」です。開発チームはderwindさん、yuminさん、Shoya Yasudaさんです。スペシャルサンクス!
使い方はTYTANとほとんど同じです。そのうちTYTANに統合される可能性があります。
インストール
Github上のパッケージを直接pipしてください。
pip install -U git+https://github.com/ShoyaYasuda/hobotanサンプル問題
5✕5の席にできるだけ多くの生徒を座らせます。ただし縦横に3席連続で座ってはいけないものとします。「3席連続で座ってはいけない」が3次の制約なのでQUBOでは解けない(*)問題です。
CPUサンプラーは SASampler() です。GPUサンプラーは MIKASAmpler() を使用します(別途pytorchをインストールしておくこと)。
import numpy as np
from hobotan import *
import matplotlib.pyplot as plt
#量子ビットを用意
q = symbols_list([5, 5], 'q{}_{}')
#すべての席に座りたい(できれば)
H1 = 0
for i in range(5):
for j in range(5):
H1 += - q[i, j]
#どの直線に並ぶ3席も連続で座ってはいけない(絶対)
H2 = 0
for i in range(5):
for j in range(5 - 3 + 1):
H2 += np.prod(q[i, j:j+3])
for j in range(5):
for i in range(5 - 3 + 1):
H2 += np.prod(q[i:i+3, j])
#式の合体
H = H1 + 10*H2
#HOBOテンソルにコンパイル
hobo, offset = Compile(H).get_hobo()
print(f'offset\n{offset}')
#サンプラー選択
solver = sampler.MIKASAmpler()
#サンプリング
result = solver.run(hobo, shots=10000)
#上位3件
for r in result[:3]:
print(f'Energy {r[1]}, Occurrence {r[2]}')
#さくっと配列に
arr, subs = Auto_array(r[0]).get_ndarray('q{}_{}')
print(arr)
#さくっと画像に
img, subs = Auto_array(r[0]).get_image('q{}_{}')
plt.figure(figsize=(2, 2))
plt.imshow(img)
plt.show()offset
0
MODE: GPU
DEVICE: cuda:0
Energy -17.0, Occurrence 844
[[1 1 0 1 1]
[1 1 0 1 1]
[0 0 1 0 0]
[1 1 0 1 1]
[1 1 0 1 1]]
Energy -17.0, Occurrence 498
[[1 1 0 1 1]
[0 1 1 0 1]
[1 0 1 1 0]
[1 1 0 1 1]
[0 1 1 0 1]]
Energy -17.0, Occurrence 538
[[1 1 0 1 1]
[1 0 1 1 0]
[0 1 1 0 1]
[1 1 0 1 1]
[1 0 1 1 0]]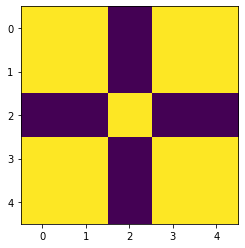
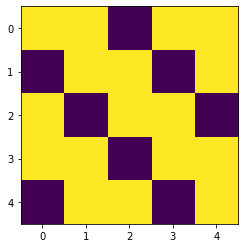
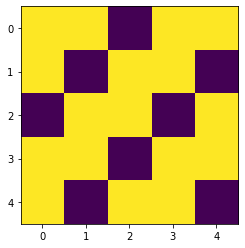
オフセットが0、17人座って-17、3席連続で座るペナルティはなしということで、エネルギー=-17の解が3種類得られました(全5種類あります)。
おわりに
これまでアニーリングと言えばQUBOしかないと思っていたのですが、有識者によると「D-waveが2次までしか対応してないだけで、一般の量子マシンでは3次以上が可能」とのことで驚きました。え?3次以上の制約も使っていいの!?
使用感、フィードバックをお待ちしています。

