やること
出来らあっ!
量子アニーリングでマインスイーパを解けるっていったんだよ!!
(中略)
え!!量子アニーリングでマインスイーパを!?

お勉強
前提知識がたくさんあります。
まず、マインスイーパを解く枠組みについては基礎編「AIワークショップ|遺伝的アルゴリズムでマインスイーパを解く」をマスターしてください。以下が含まれます。
- 画面キャプチャ
- 配列操作(マスク操作)
- 遺伝的アルゴリズム(GA)での安全マス計算
- 自動クリック

このコードの3の部分を量子アニーリングでの計算に置き換えます。
基礎編の結果はこちらの記事にもまとめてあります。
量子アニーリング(D-wave)の基本的な使い方はこちらを参照。
このとき、量子ビットの定義や条件式の設定を手でやっていると大変なので、関数化はこちらを参照。
そして、(21-3の内容と重複しますが)量子アニーリングで何ができるかをまとめたのがこちら。今回は「n個の量子ビットからm個を1にする」のパターンだけを使います。
実行環境
画面キャプチャを行うため、「Google Colab」「Jupyter Notebook」のようなクラウド的な環境は使えません。実行する場合はPCにPython3系の実行環境を用意する必要があります。
WinPython3.6をおすすめしています。
量子アニーリングでどうやるか(ざっくり)
基礎編をマスターしている前提でざっくり説明します。
注目マス(5つ)に量子ビットを割り当てます。注目マスに関係がある数字マス(5つ)についてそれぞれ条件式を立てます。
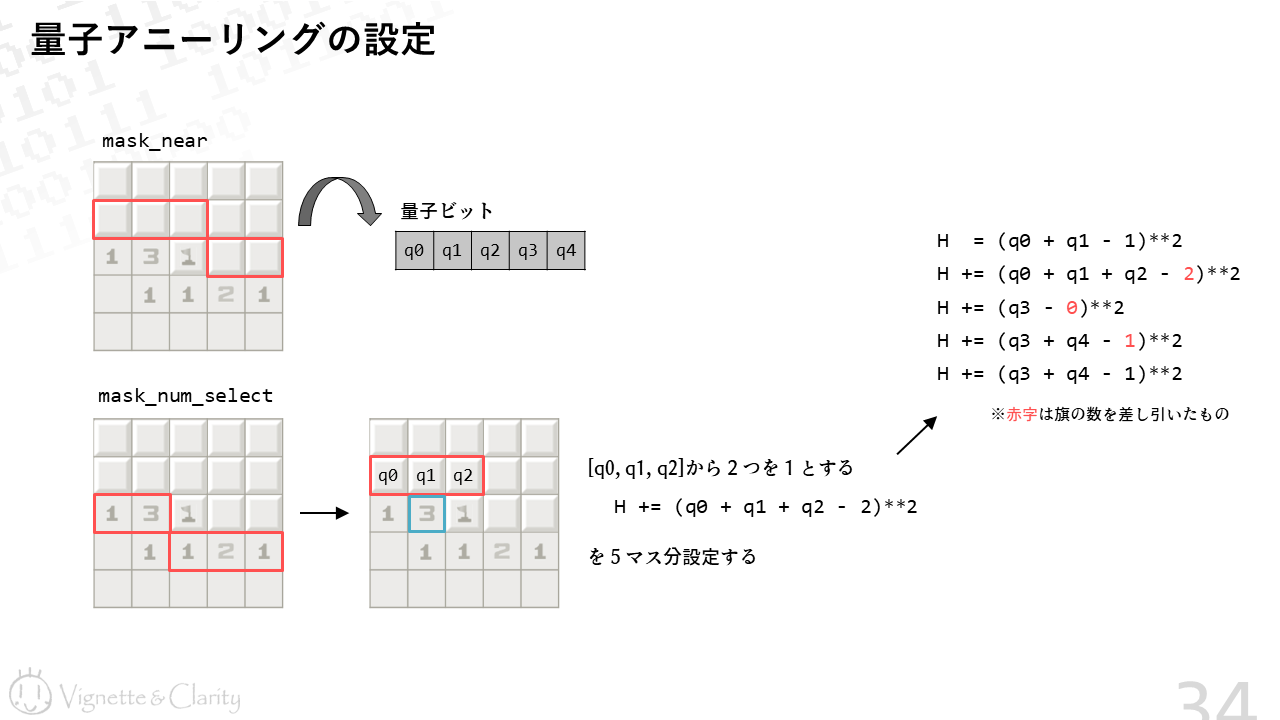
例えば「3」の数字は、q0, q1, q2 の中から2つが1になれば良いことを意味しています(旗があるので3つではなく2つ)。よって条件式に以下を追加することになります。
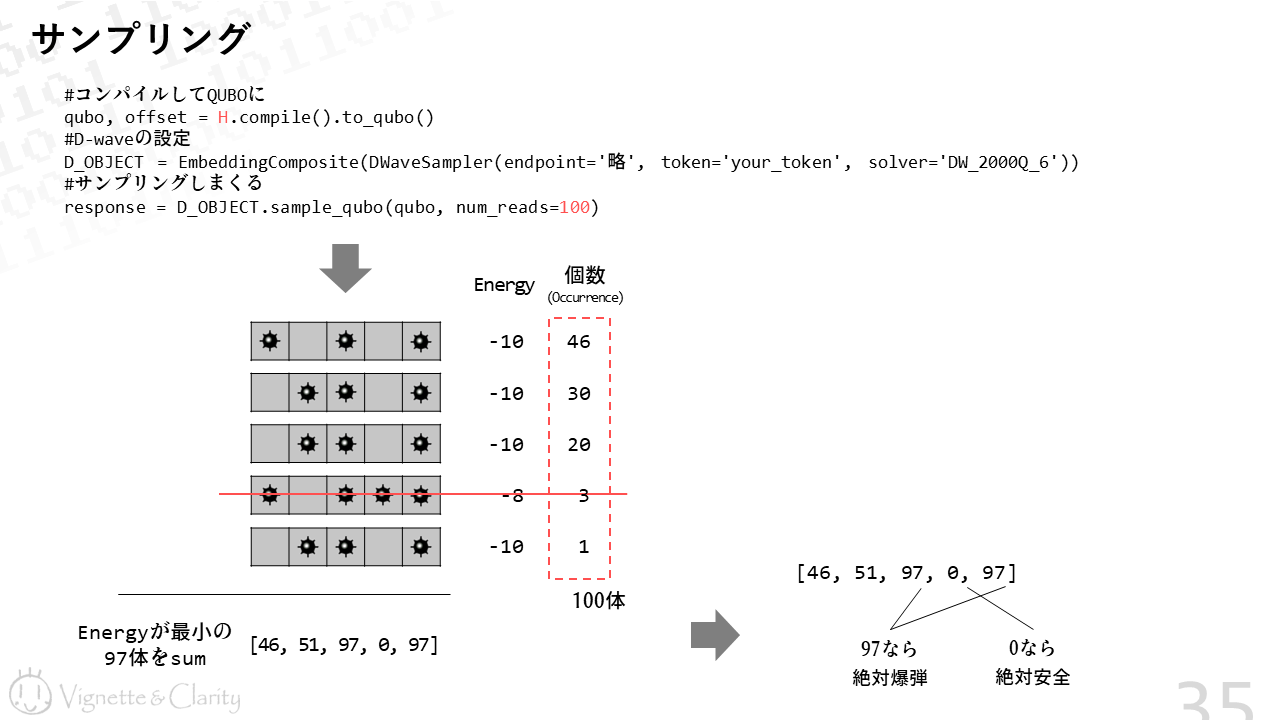
H += (q0 + q1 + q2 - 2)**2サンプリングした結果にはEnergyとOccurrenceが付いています。Energyが最小の解だけに注目して、OccurrenceをGAの「個体数」として集計します。あとは共通の処理です。
コード
インポートと条件記述関数を置きます。
from dwave.system.composites import EmbeddingComposite
from dwave.system.samplers import DWaveSampler
from pyqubo import Binary
#条件を記述する関数
def H_add(qbits, num):
command = '(' + '+'.join(['q{:03}'.format(i) for i in qbits]) + '-{})**2'.format(num)
print(command)
return eval(command)コードの中の「#GA~」で囲まれた部分を置き換えます。
変更前↓
#----- GA -----
#パラメータ範囲
near_num = np.sum(mask_near)
para_range = [[0, 1]] * near_num
print(para_range)
#多様性がなくなるまで(自動停止するまで)集団を最適化
myopt = vcopt()
para, score = myopt.dcGA(para_range, #パラメータ範囲
get_score, #評価関数
-1, #目標値(到達不可能)
show_pool_func='print', #Noneで非表示
pool_num=None) #100とか指定しても良いけど
#評価値0に達していなければ終了
if score > 0:
print('GA err')
break
#集団を取得
pool = myopt.pool
#集団のスコアを調べてスコア0の個体のみに絞る
scores = np.array([get_score(para) for para in pool])
print(scores)
pool = pool[scores==0]
print(pool)
#-------------変更後↓(for中のためインデントが入っていることに注意)
#----- 量子アニーリング -----
#隣接マスの個数の量子ビットを定義
near_num = np.sum(mask_near)
for i in range(near_num):
command = 'q{:03} = Binary(\'q{:03}\')'.format(i, i)
print(command)
exec(command)
#量子ビット番号の配列(他は-1)
f_qbit = np.where(mask_near==True, 0, -1)
f_qbit[f_qbit==0] = range(near_num)
print(f_qbit)
#条件対象の数字部分マスク
mask_near_expand = signal.convolve2d(mask_near, g, mode='same', boundary='fill', fillvalue=0) > 0
mask_num_select = mask_near_expand * mask_num
print(mask_num_select)
#条件対象の数字の個数の条件を記述
H = 0
ij_list = np.array(np.where(mask_num_select==True)).T
for k, (i, j) in enumerate(ij_list):
#print('~~~~~~~~~~~~~~~')
#print(i, j)
#条件の数字部分だけのマスク
mask_tmp = np.zeros(f.shape, bool)
mask_tmp[i, j] = True
#それと関係がある隣接マスク
mask_tmp_expand = signal.convolve2d(mask_tmp, g, mode='same', boundary='fill', fillvalue=0) > 0
mask_near_select = mask_tmp_expand * mask_near
#print(mask_near_select)
#関係がある量子ビット番号リスト
qbits = f_qbit[mask_near_select]
print(qbits)
#隣接の旗の数
flag_num = np.sum(mask_tmp_expand * mask_flag)
print(-flag_num)
#式
H += H_add(qbits, f_num[i, j] - flag_num)
#コンパイル
model = H.compile()
qubo, offset = model.to_qubo()
print('qubo\n{}'.format(qubo))
#D-waveの設定
sampler = EmbeddingComposite(DWaveSampler(endpoint='https://cloud.dwavesys.com/sapi',
token='your_token',
solver='DW_2000Q_6'))
#サンプリングしまくる
response = sampler.sample_qubo(qubo, num_reads=1000)
#最小エネルギーをチェック
print('response')
best_energy = 999
for (sample, energy, occurrences, _) in response.data():
print('Sample:{} Energy:{} Occurrences:{}'.format(list(sample.values()), energy, occurrences))
if energy < best_energy:
best_energy = energy
#best_sample = np.array(list(sample.values()))
print(best_energy)
#最小エネルギーの配列を集める(Occurrencesの数だけ複数入れる)
pool = []
for (sample, energy, occurrences, _) in response.data():
if energy == best_energy:
for i in range(occurrences):
pool.append(list(sample.values()))
pool = np.array(pool)
print(pool)
#-------------‘your_token’ には各自のトークンを入れてください。
結果
初級2つ、中級2つ、おまけに中級の失敗1つを動画にまとめました。
上級はやらないの?
上級は運ゲー要素が強いためGA版でも成功率が低く、かつ、上級ではサンプリング数を1000より大幅に増やす必要があります。失敗しているうちにLeapの月間計算時間1分を超えてしまうため断念しました。