やること
前回、量子アニーリングで巡回セールスマン問題を解きました。
距離に比例したペナルティをコスト関数として設定しましたが、ペナルティ(コスト)の値には距離の10分の1を用いました。これは制約条件よりもコスト関数の規模を小さくし、あくまで制約条件を優先的に満たした解を得るためです。
QUBOで問題を解くには、このようにコスト関数に0.1をかけたり、逆に制約条件に10をかけたりして両者のバランスを調整する必要があります。今回はこのバランス調整においてどんな値をかければよいかを考察します。
準備
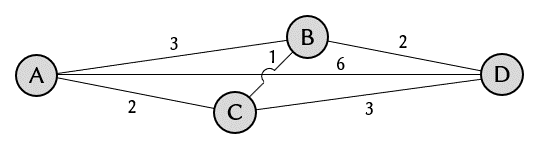
問題については前回の記事を参照ください。図だけ再掲します。
前回のコードを改造しました。制約条件とコスト関数を別で定義し、コンパイル前にコスト関数に係数k をかけて合体します。このコードだけでは動かないのでご注意。
#1番目に訪れる都市は1つだけにしたい、のやつ
H1 = 0
H1 += (q00 + q01 + q02 + q03 - 1)**2
H1 += (q04 + q05 + q06 + q07 - 1)**2
H1 += (q08 + q09 + q10 + q11 - 1)**2
H1 += (q12 + q13 + q14 + q15 - 1)**2
#都市Aに訪れる都市は1つだけにしたい、のやつ
H1 += (q00 + q04 + q08 + q12 - 1)**2
H1 += (q01 + q05 + q09 + q13 - 1)**2
H1 += (q02 + q06 + q10 + q14 - 1)**2
H1 += (q03 + q07 + q11 + q15 - 1)**2
#都市間の距離に比例したペナルティ
#1番目から2番目への移動について
H2 = 0
H2 += 0 * (q00 * q04) #距離0なので
H2 += 3 * (q01 * q04) #距離3なので
H2 += 2 * (q02 * q04) #距離2なので
H2 += 6 * (q03 * q04) #距離6なので
H2 += 3 * (q00 * q05)
H2 += 0 * (q01 * q05)
H2 += 1 * (q02 * q05)
H2 += 2 * (q03 * q05)
H2 += 2 * (q00 * q06)
H2 += 1 * (q01 * q06)
H2 += 0 * (q02 * q06)
H2 += 3 * (q03 * q06)
H2 += 6 * (q00 * q07)
H2 += 2 * (q01 * q07)
H2 += 3 * (q02 * q07)
H2 += 0 * (q03 * q07)
#2番目から3番目への移動について
H2 += 0 * (q04 * q08)
H2 += 3 * (q05 * q08)
H2 += 2 * (q06 * q08)
H2 += 6 * (q07 * q08)
H2 += 3 * (q04 * q09)
H2 += 0 * (q05 * q09)
H2 += 1 * (q06 * q09)
H2 += 2 * (q07 * q09)
H2 += 2 * (q04 * q10)
H2 += 1 * (q05 * q10)
H2 += 0 * (q06 * q10)
H2 += 3 * (q07 * q10)
H2 += 6 * (q04 * q11)
H2 += 2 * (q05 * q11)
H2 += 3 * (q06 * q11)
H2 += 0 * (q07 * q11)
#3番目から4番目への移動について
H2 += 0 * (q08 * q12)
H2 += 3 * (q09 * q12)
H2 += 2 * (q10 * q12)
H2 += 6 * (q11 * q12)
H2 += 3 * (q08 * q13)
H2 += 0 * (q09 * q13)
H2 += 1 * (q10 * q13)
H2 += 2 * (q11 * q13)
H2 += 2 * (q08 * q14)
H2 += 1 * (q09 * q14)
H2 += 0 * (q10 * q14)
H2 += 3 * (q11 * q14)
H2 += 6 * (q08 * q15)
H2 += 2 * (q09 * q15)
H2 += 3 * (q10 * q15)
H2 += 0 * (q11 * q15)
#制約条件とコスト関数の合体
H = H1 + k*H2得られる解
このあとに出てくる2つの解を予習しておきます。
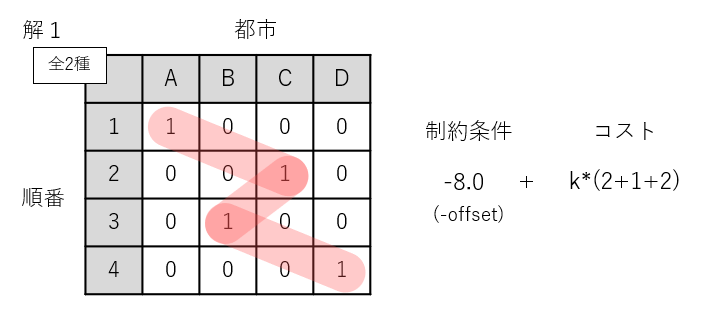
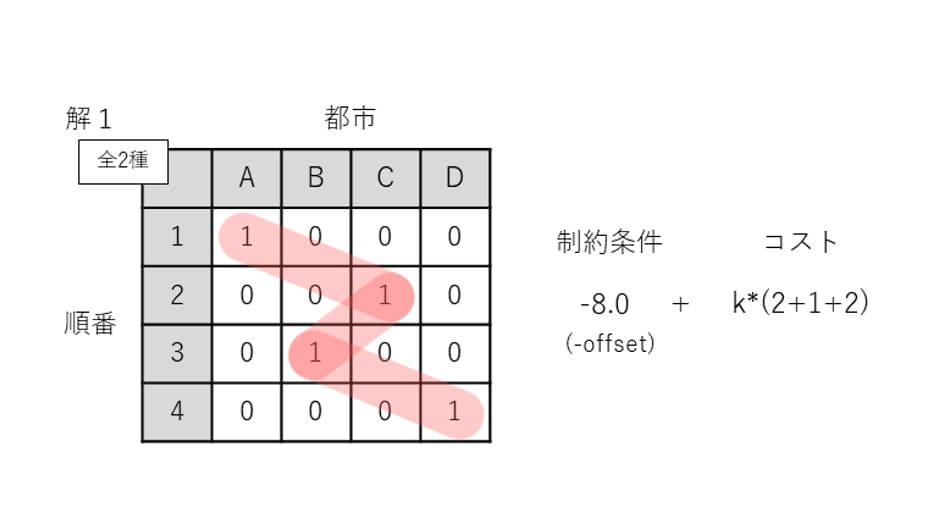
解1は制約条件をすべて満たしている最適解です。制約条件をすべて満たしている場合、制約条件によるエネルギーは-8.0です。「4個の量子ビットから1個を1にする」が1式あたり-1.0、これが8式で-8.0です。ちなみに「2個を1にする」は1式あたり-4.0、「3個を1にする」は1式あたり-9.0の計算です。コスト関数によるエネルギーはk*5.0です。
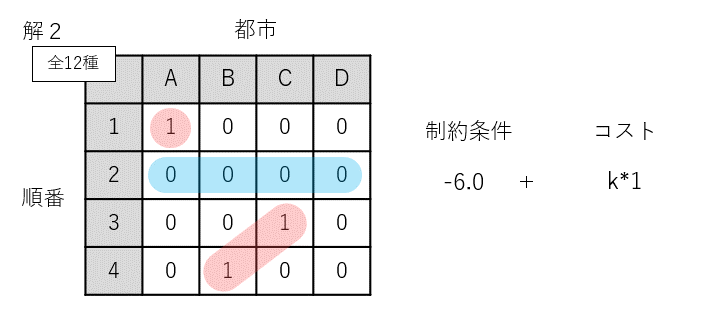
解2は制約条件を2つ諦めた準最適解です。諦めた分、制約条件によるエネルギーは-6.0に。一方、諦めたおかげでコストはk*1.0に下がります。
実験
コスト関数にかける係数kを変えながら、SASampler(shot=1000)を10回ずつ実行して「制約条件を守った解が得られる確率」を調べました。shot=1000は十分に良い解が得られる数です。
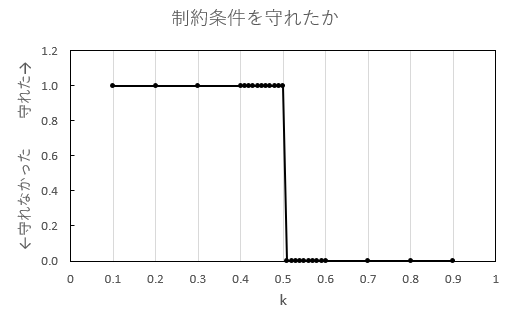
結果、k=0.50が境界であることがわかりました。
詳しく考察
k=0.49のとき、解1が単独一位として得られます。
解1:-8.0 + 0.49*(2+1+2) = -5.55
解2:-6.0 + 0.49*1 = -5.51
k=0.50のとき、解1と解2が同率一位で得られます。
解1:-8.0 + 0.50*(2+1+2) = -5.5
解2:-6.0 + 0.50*1 = -5.5
結局、制約条件に妥協が起きるとエネルギーは2.0上がり、コスト関数はk*(道路2本分の距離)下がるという取り引きが行われます。
我々が関心を持っているkを見積るには、
k*(道路2本分の距離) < 2.0
を満たす最大のkを求めればよいことになりますが、どの道路に着目すべきかは簡単には分かりません。そこでもう少し粗く見積もることにして、
k*(最長の道路の距離) < 1.0
としても良いでしょう。今回の問題では
k×6 < 1.0
より、kはだいたい0.1で良いことがわかります。
なお、kが小さすぎると、つまり制約条件を優先しすぎると制約ギリギリの領域の探索が甘くなり、大域解を逃すリスクが高まることが予想されます。あまり調子に乗って0.001とかにしないほうが良いでしょう。
おわりに
この係数kをハイパーパラメータとして探索したいという要望もあるようですが、類似の問題を繰り返し解くようなシチュエーションでもない限り、そのような予備探索はできるだけ避けたいことだと思っています。なぜなら、それを探索する余力があれば本番の探索アルゴリズム(SAやらGAやら)に計算リソースを回したほうが良いからです。kは理論上そこそこな数値を入れておいて、あとは時間が許す限りSAのパワーを上げて祈る。こういうものではないでしょうか。