はじめに
2024/05/13追記
バグ報告を受けて一部修正しました。pgmpyは最新版ではなくpgmpy==0.1.14をインストールするようにしてください(その上でさらに注意点があります)。
こんにちは、hiranumaです。
今回はpythonで「pgmpy」というライブラリを使って観測データからベイジアンネットワークを構築して、構築したネットワークから新たなデータをサンプルしてみようと思います。
ベイジアンネットワークを使う機会があったのですが、調べても該当する記事が無かったり、さまざまなライブラリがある中で僕がやりたいこととマッチするものがうまく見つからなかったため、今後ベイジアンネットワークを使う人や僕自身のメモのために残そうと思います。本記事はベイジアンネットワークってなんぞや、という人から、ベイジアンネットワーク使おうとしているけどいまいちプログラムが書けないという人を想定しています。
ベイジアンネットワークとは
そもそも、ベイジアンネットワーク(以下、BN)とは、さまざまな物事の因果関係をグラフとして表わして視覚的に理解することができ、かつ、物事の関係性を確率で表すことができる非循環有向グラフ(以下、DAG)です。ざっくりいうとベイズの定理によるグラフ構造ですね! (DAGとは、ネットワーク間に矢印があり、矢印をたどっても絶対にループがないグラフのこと。)
これだけで、BNを理解できた人は天才です。僕には呪文にしか感じませんでした。。例えば、以下のようなネットワークがあったとします。
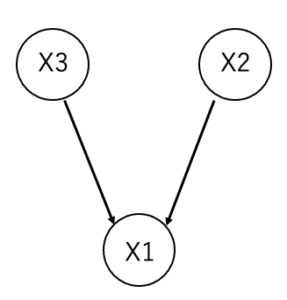
X1, X2, X3の丸のことをノードといい、ノードから出ている矢印のことを辺、もしくはエッジと言います。BNでは、各ノードが確率変数になっていて、例えば、事象X1が起こる確率は事象X2と事象X3に依存していることがわかります。
今、以下の図のような確率がわかっているとします。
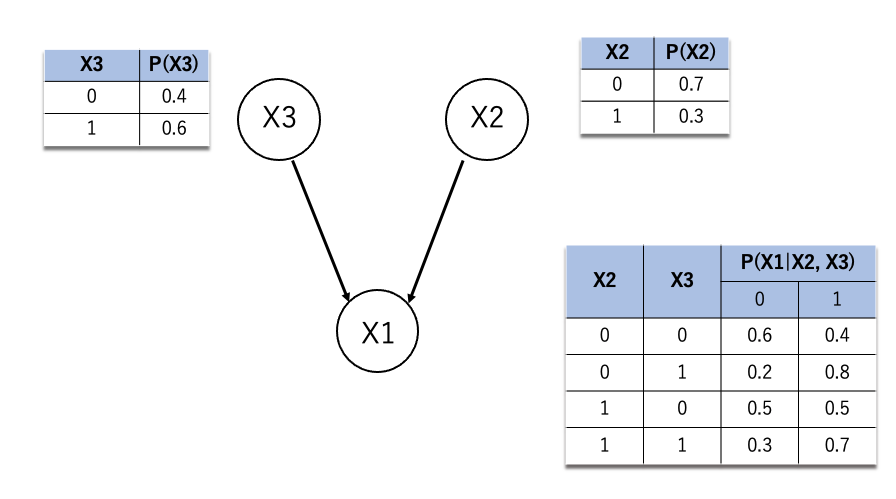
右上は「X2の0,1の確率」、左上は「X3の0,1の確率」、右下は「X2, X3がわかった時のX1の0,1の確率」を意味しています(1=起きた, 0=起きていない)。この表のことを条件付き確率表(CPD)といいBNではこの表とネットワークの構造がわからないとなにもできません。
BNのうれしいことはX1がわかった時に原因がX2なのかX3なのか確率的に予測できるという点です。
ベイズの定理を使って原因を探る
では、ベイズの定理を使ってX1が1だとわかった時に、それが何が原因である確率が高いのか調べたいと思います。
まず、P(X1=1)の確率を知りたいので、周辺化します。
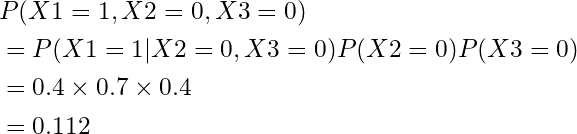
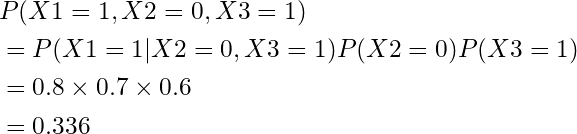
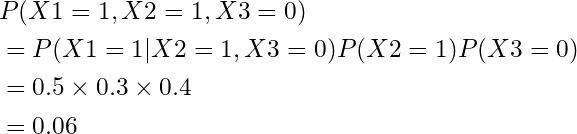
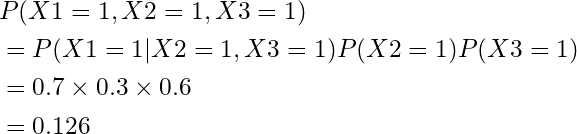
![]()
周辺化できたので、実際に各確率を計算してみます。
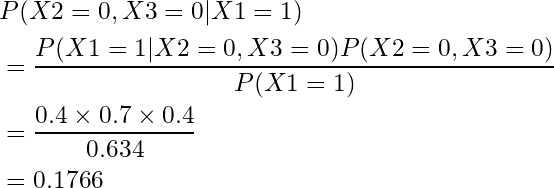
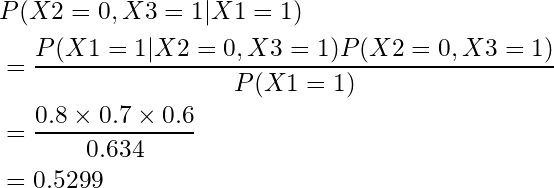
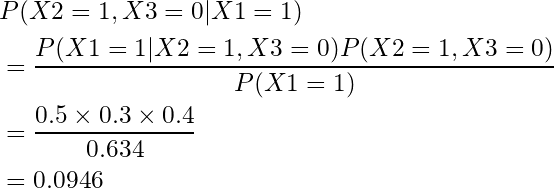
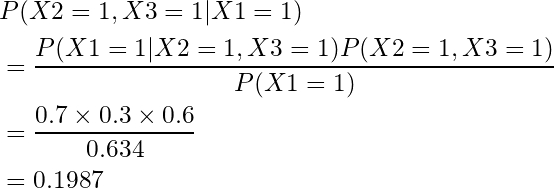
以上より、
![]()
が一番確率が高いことがわかるので、X1が起きた時に53%程度の確率でX3が原因であるということがわかりました。BNの恩恵はわかりましたでしょうか?
ベイジアンネットワークの構築
以上の例は、BNが事前にわかっているため利用することができました。BNの構造がわかっていない状態ではどうするのか、構築方法について一例を紹介します。
BNの構築方法は主に2つの要素に分けられます。
- 評価指標
- 良いネットワークの探索
この2つの要素を決定して探索します。1の評価指標とはネットワークの良し悪しを決める評価値で学習データに対してどの程度そのネットワークが良いのかを比べることができます。2の探索はさまざまなネットワークを構築してよりよいネットワークを探すといった探索行為になります。このネットワークに対する評価方法や探索方法はさまざまな研究が行われているので、興味がある人は調べてみてください。
pgmpyには
- BDeu Score
- Bic Score
- K2 Score
という評価基準があります。ざっくりいうと、BDeuとはBayesianDirichlet(BD)という評価方法に必要な事前知識を事前分布に与えることが難しいのでそれをうまく拡張した手法で評価します。BICとはベイズ情報量基準(Bayesian Information Criterion)のことでベイズ情報量基準にしたがって評価します。K2 Scoreは先程のBDという評価基準の特定のバージョンのことです。(違ったらごめんなさい。。)
また、探索方法としてpgmpyには
- Exhaustive Search
- Hill Climb Search
が用意されています。1は全探索でノードが6以上になると計算量が膨大になり実行できません。2は山登り法で近隣のネットワークの中で最適な解を探索してくれます。
では、実際にプログラムを書いていきましょう!
ネットワークの推定
まず、今回使用するライブラリpgmpyをインストールします。condaやcolabの方はそれぞれcondaや!pipでインストールしてください。
2024/05/13コード修正(バージョン指定)
pip install pgmpy==0.1.14適当なネットワークを仮定してデータを作成します。「X1=X2+X3」となるようなデータです。
import numpy as np
import pandas as pd
from pgmpy.estimators import K2Score, HillClimbSearch, ExhaustiveSearch
from pgmpy.sampling import BayesianModelSampling
from pgmpy.models import BayesianModel
# データ生成
data = pd.DataFrame(np.random.randint(0, 2, size=(5000, 3)), columns=['X1', 'X2', 'X3'])
data['X1'] = data["X2"] + data["X3"] # X3 -> X1 <- x2
print(data) X1 X2 X3
0 0 0 0
1 2 1 1
2 2 1 1
3 0 0 0
4 1 1 0
... .. .. ..
4995 2 1 1
4996 0 0 0
4997 1 0 1
4998 2 1 1
4999 2 1 1では、データを元にK2Scoreを使った山登り法でネットワークを推定します。
# データを使ってネットワークを推定
network = HillClimbSearch(data, scoring_method=K2Score(data))
best_network = network.estimate()
edges = best_network.edges()
nodes = best_network.nodes()
print(edges)
print(nodes) 0%| | 2/1000000 [00:00<2:38:19, 105.27it/s]
[('X2', 'X1'), ('X3', 'X1')]
['X1', 'X2', 'X3']これでネットワークの構築ができました。(‘X2’, ‘X1’) は (‘親’, ‘子’) の関係なので、X2→X1、X3→X1と想定通りのネットワークであることがわかります。
2024/05/13追記
このネットワーク推定のステップでは、確率で「仮定通りの正しいネットワーク」と「それ以外のネットワーク」が得られます(要素が少なすぎるから?)。ここでは上記の「正しいネットワーク」が出るまでガチャを回してください。ネットワークを手動で定義する場合はこの混乱とは無縁です。
条件付き確率表(CPD)を求める
ここまではネットワークbest_networkにはまだCPDが計算されておらず、構築したインスタンスbest_networkのクラスであるDAGモデルではCPDを求めることはできません。なので、構築したネットワークを使って別のクラスでCPDを求める必要があります。
ここでBayesianModelというクラスを使います。
# 探索したネットワークのエッジからネットワークのモデルを構築してCPDを求める
model = BayesianModel(list(edges))
# 独立なノードが入っていない場合にも対応
model.add_nodes_from(list(nodes))
model.fit(data) # cpds を計算
cpds = model.get_cpds()
for cpd in cpds:
print(cpd, '\n')+-------+-------+-------+-------+-------+
| X2 | X2(0) | X2(0) | X2(1) | X2(1) |
+-------+-------+-------+-------+-------+
| X3 | X3(0) | X3(1) | X3(0) | X3(1) |
+-------+-------+-------+-------+-------+
| X1(0) | 1.0 | 0.0 | 0.0 | 0.0 |
+-------+-------+-------+-------+-------+
| X1(1) | 0.0 | 1.0 | 1.0 | 0.0 |
+-------+-------+-------+-------+-------+
| X1(2) | 0.0 | 0.0 | 0.0 | 1.0 |
+-------+-------+-------+-------+-------+
+-------+--------+
| X2(0) | 0.4994 |
+-------+--------+
| X2(1) | 0.5006 |
+-------+--------+
+-------+--------+
| X3(0) | 0.5072 |
+-------+--------+
| X3(1) | 0.4928 |
+-------+--------+ 2024/05/13追記
出力の読み方を説明します。真ん中はX2について、単体で湧き出る(0と1が約50%ずつ)ことを意味しています。下部も同様にX3について、他に影響されず湧き出る(0と1が約50%ずつ)と言っています。上部はX1について、X2とX3の状態に応じてこんな確率で決まりますよと。元データのX1は正確にX2+X3の値だったため、表中の確率がすべて1.0であることは合点がいきます。
これでCPDを求めることができました。あとは使い道に合わせてカスタマイズすればさまざまな問題に対応できます。
ベイジアンネットワークから新たなデータを生成
僕はこの構築したネットワークから新たなデータをサンプルする必要がありました。サンプル方法にもさまざまなクラスが用意されているのでドキュメントを参照してみてください。今回はBayesianModelSamplingというクラスを用います。
# サンプリング
sampler = BayesianModelSampling(model)
new_data = sampler.forward_sample(size=10)
print(new_data)Generating for node: X1: 100%|██████████| 3/3 [00:00<00:00, 1497.97it/s]
X2 X3 X1
0 1 1 2
1 1 0 1
2 0 1 1
3 1 1 2
4 1 0 1
5 0 1 1
6 1 0 1
7 0 1 1
8 0 0 0
9 1 1 2新たなデータが生成されました。ここで注意するのがサンプルデータのcolumnsの順序です。BNのサンプルは親のいないノードから確率的に生成するので、順序がX1, X2, X3ではないことがわかります。このnew_dataはpandasのDataFrameになっているので、入れ替えるのは容易にできます。
まとめ
今回はベイジアンネットワークを使うことがあったのでpgmpyというライブラリを使って説明しました。今回紹介したやり方だけでなく、ネットワークに対してある事象がわかった時の原因を探ることもできます。詳しくはドキュメントを参照してみてください。本記事はpgmpyを使った時に学習したネットワークからどうやってCPDを計算するのか、そして新たなデータをサンプルするのかを試行錯誤の上で見つけた一つの方法になります。別の方法があればSlackやTwitterでご連絡いただけると嬉しいです。