はじめに
ボールを始点からより低い高さにある終点まで転がして移動させるとき、どんな坂を使うと速いのか。ただし摩擦や空気抵抗はないものとする。摩擦がないため正確には「転がす」ではなく「重力に従って移動させる」という話になります。これは最速降下問題と呼ばれ、サイクロイド曲線が最速であることが証明されています。
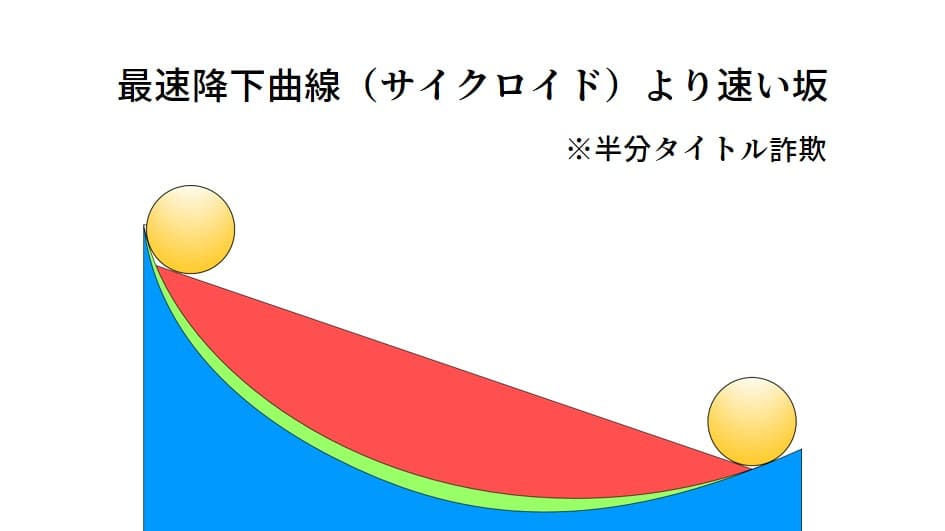
物理実験としても楽しまれているテーマなのですが、実は「サイクロイドの坂が最速である」は誤りです。例えば次のような比較実験をYoutubeで見たことがあるかと思います。

繰り返しになりますが摩擦や空気抵抗はなしです。緑の坂はサイクロイドですが、これよりも速い坂があるという話をしたいと思います。物理に明るい方であればもうオチが予想できていますかね( ̄∇ ̄; )
参考文献
最速=サイクロイドの証明は物理のかぎしっぽをご参照ください。
実際に確認してみた
小生意気な動画にしてみました。
たねあかし
これみよがしに巨大なボールを使ったので分かったかと思いますが、緑の坂はサイクロイド曲線、青い特別な坂は「ボールの中心がサイクロイドの軌跡となる坂」です。
数学的な証明は質点(体積のない点)を前提としているため、ボールを使う場合はボールの中心がサイクロイドになるかが重要です。ボールの大きさが無限小であればサイクロイド坂が最速ですが、半径が大きいほどずれてくるわけですね。
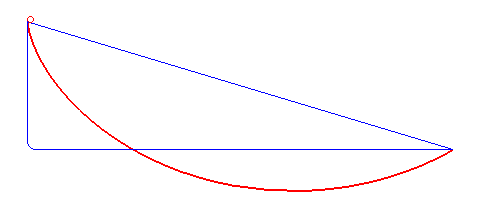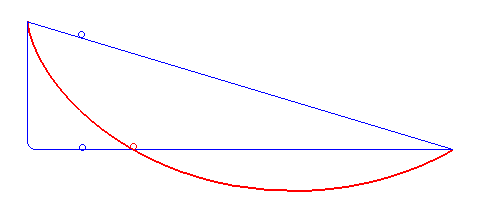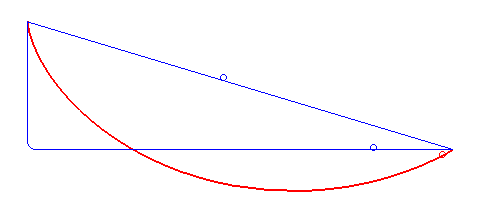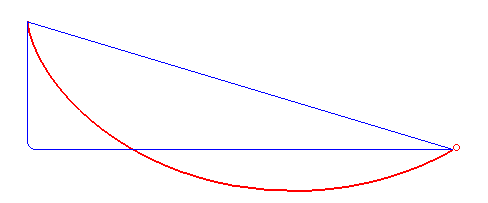
他のYoutube動画の確認
こちらのシミュレーションはサイクロイド坂にボールを置いているため最速にならないですが、ボールに対して坂を極端に大きくすることで誤差を小さくしています。
こちらも最速にはならないパターンです。
補足として、坂にボールを置くタイプのシミュレーションのすべてが誤りとは言い切れません。例えば坂上の質点から仮想的にボールを投映している場合はきちんとサイクロイドが最速になります(ボールが重力に従って運動しているとは言えなくなりますが)。あるいは、サイクロイドと言いつつ先の「特別な坂」と同じ設計であればもちろん最速です。
次の動画も最速ではないパターンです。(摩擦と空気抵抗を無視したとしても)
おわりに
タイトルから一貫してサイクロイドの「坂」と言っていたのはこのためでした。半分タイトル詐欺ですが、半分真面目でしたね。
なぜこんな検証をしたかというと、科学教室のお手伝いをしていると「それYoutubeで見た」という子どもたちが多いのです。もともと教育熱心なご家庭が集まるわけですから、大抵の実験はYoutubeで視聴済みというわけです。なんなら倍速で見ているかもしれません。様々なコンテンツが高速で消費されていきます。
そんな時代だからこそ、当たり前を疑う力をつけ、自分の手で確かめてほしいと思っています。その過程で必要になる技術(計算、シミュレーション、工作など)を興味を持って習得することは苦になりませんし、学ぶことの楽しさを感じられると思います。
ビネクラは科学教室のお手伝いをしています。こちらのページの下部にこれまでの開催を列挙していますのでよければご覧ください(宣伝)。