やること
「Deepでポン」という表現を耳にしました。調べても定義が見つからなかったので私なりに定義してみます(間違っていたらご指摘ください・・・)。
「Deepでポン」は「とりあえずDeep Learningでポンっと結果を出してみる」の意味。Deep Learningの便利さ、魔法のような様子を表現している(cf.ミルモでポン!)。「課題の本質を理解せずにDeep Learningしてるけどもっと適切なアプローチあっただろ」という戒めのニュアンスを含む場合がある。
何かを推定するモデルを構築するとき、とりあえず多項式近似するか、深層学習(ブラックボックス)でポンするか、数理モデル(ホワイトボックス)を構築するか、迷うことがあるでしょう。今日は単純な題材を用いて、多項式近似と深層学習と数理モデル化の違いを考察してみます。
参考文献
サクッと深層学習はこちらもご参照ください。
実行環境
WinPython3.6をおすすめしています。
Google Colaboratoryが利用可能です。

pip install
グラフに日本語を表記するために必要です。
pip install japanize-matplotlibたこ焼きの値段
あるたこ焼き屋さんでは、次のようなまとめ買い割引を行っています。

| 個数 | 価格 |
| 1~10個目 | 50円/個 |
| 11~20個目 | 40円/個 |
| 21個目~ | 30円/個 |
| 容器 | 1舟に6個まで入る 50円/舟 ただし31個目以降は容器無料 |
例えば7個買うと、たこ焼き350円+容器100円=450円になります。1~50個買ったときの金額をプロットしてみます。
import numpy as np
import numpy.random as nr
import matplotlib.pyplot as plt
import japanize_matplotlib
from keras import optimizers
from keras.models import Sequential
from keras.layers.core import Dense
#金額計算関数
def calc_price(num):
price = 0
#たこ焼き
for i in range(num):
if i <= 10:
price += 50
if 10 < i <= 20:
price += 40
if 20 < i:
price += 30
#容器
price += min((1 + (num - 1)//6) * 50, 250) #31個以上は250円固定
return price
#===================
# 正解の確認
#===================
#個数の列
nums = np.arange(1, 51)
#金額計算
prices = np.array(list(map(calc_price, nums)))
#グラフ表示
plt.plot(nums, prices, 'ok', label='正解')
plt.legend()
plt.show()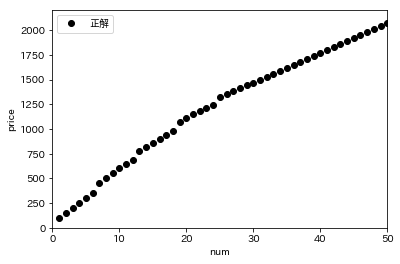
ただしこれは神のみぞ知る真の数理モデルですので、知らないという前提でいきます。
サンプルデータの生成
無作為に選ばれた10人(=N)のお客さんに対して出口調査を行い、「買った個数(=x_sample)」と「支払い金額(=y_sample)」を聞いたところ、次のようになりました。
#===================
# サンプルデータの生成と確認
#===================
#乱数シード固定
nr.seed(0)
#テストデータの生成
N = 10
x_sample = nr.randint(1, 51, N)
#金額計算
y_sample = np.array(list(map(calc_price, x_sample)))
#グラフ表示
plt.plot(x_sample, y_sample, 'ok', label='サンプル(N=10)')
plt.legend()
plt.show()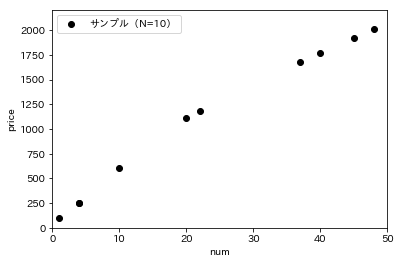
このデータを用いて、個数(=x)から金額(=y)を推定するモデルを構築します。多項式近似として1次関数、2次関数、3次関数を用います。深層学習は中間層のユニット数=10のモデルとユニット数=100のモデルの2種類を比較します。
各モデルで近似 / 学習
詳細はコード参照ですが。
#===================
# 各モデルで学習
#===================
#1次関数で近似(y=ax+b)
a, b = np.polyfit(x_sample, y_sample, 1)
#近似した線
y_1 = a*nums + b
#2次関数で近似(y=ax^2+bx+c)
a, b, c = np.polyfit(x_sample, y_sample, 2)
#近似した線
y_2 = a*(nums**2) + b*nums + c
#3次関数で近似(y=ax^3+bx^2+cx+d)
a, b, c, d = np.polyfit(x_sample, y_sample, 3)
#近似した線
y_3 = a*(nums**3) + b*(nums**2) + c*nums + d
#深層ニューラルネットで近似(中間層のユニット数3)
#学習データ
x_train = x_sample.reshape((N, 1))
y_train = y_sample.reshape((N, 1)) / 2000
#NNモデル
model = Sequential()
model.add(Dense(10, input_dim=1, activation='tanh'))
model.add(Dense(1, activation='linear'))
Adam = optimizers.Adam(lr=0.001)
model.compile(loss='mse', optimizer=Adam)
#学習
model.fit(x_train, y_train, nb_epoch=1000, verbose=0)
#推測した線
y_4 = model.predict(nums) * 2000
#深層ニューラルネットで近似(中間層のユニット数100)
#NNモデル
model2 = Sequential()
model2.add(Dense(100, input_dim=1, activation='tanh'))
model2.add(Dense(1, activation='linear'))
Adam = optimizers.Adam(lr=0.001)
model2.compile(loss='mse', optimizer=Adam)
#学習
model2.fit(x_train, y_train, nb_epoch=1000, verbose=0)
#推測した線
y_5 = model2.predict(nums) * 2000
#グラフ表示
plt.plot(x_sample, y_sample, 'ok', label='サンプル(N=10)')
plt.plot(nums, y_1, '-', label='1次関数')
plt.plot(nums, y_2, '-', label='2次関数')
plt.plot(nums, y_3, '-', label='3次関数')
plt.plot(nums, y_4, '-', label='深層学習(ユニット8)')
plt.plot(nums, y_5, '-', label='深層学習(ユニット100)')
plt.legend()
plt.show()
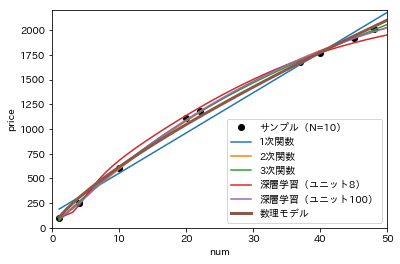
どうでしょうか?どれも似たりよったりですが、1次関数がちょっと合っていないなという印象を受けます。
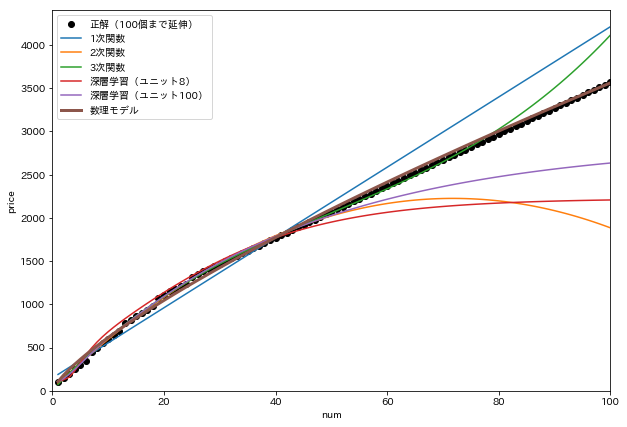
未知のデータをどこまで予測できるか、これらの線を x=100 まで延伸してみます。

80個くらいまでは3次関数が優秀に見えます。
さらにこれらの線を x=200 まで延伸してみます。
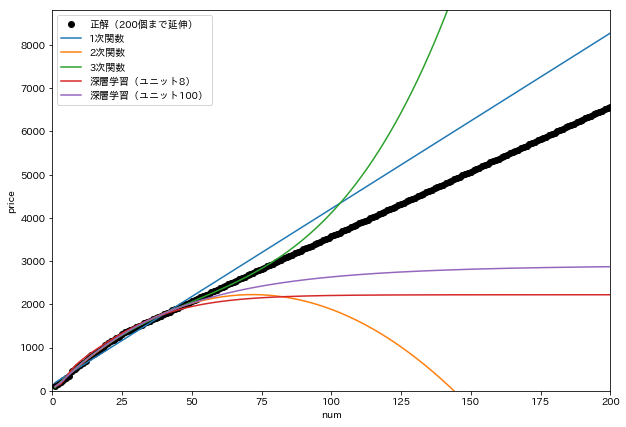
たこ焼きを200個も買う人がいるか分かりませんが、一周回って1次関数がまともに見えます。
数理モデルを立てる
ここで数理モデルを立ててみます。ヒントとして
- 個数が増えるほど金額も上がるだろう(→単調増加関数)
- まとめ買いすると少し割引があるだろう(→傾きは減少していく)
と考え、y=ax^b(0<b<1)を採用することにします。任意の関数近似は以下のように実装します。
from scipy.optimize import curve_fit
#数理モデル
def func(x, a, b):
return a*x**b
#近似
(a_6, b_6), _ = curve_fit(func, x_sample, y_sample)
#近似した線
y_6 = func(nums, a_6, b_6)さっきのグラフに数理モデルを追加しました。ちょっと見づらいですが。
x=100 まで延伸してみると、数理モデルがいかにフィットしているかが分かります。
さらにこれらの線を x=200 まで延伸してみます。
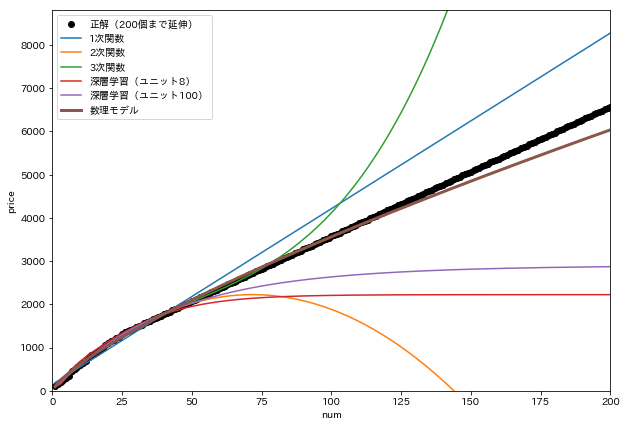
200個買ってもなかなかの精度で予測できています。わずか10個の学習データからとは思えない推定精度ではないでしょうか。
まとめ
今回は、10個の学習データしか得られない状況で次の3つのアプローチで近似 / 学習してみました。
多項式近似
とりあえず思考停止で近似しました。いずれも良くありませんが、1次関数は「個数が増えるほど金額も比例的に上がる」という原理に則っているため比較的筋が良かったです。
深層学習
学習データが少なすぎてまったく不適切でした。(学習データは少なくとも1000セット以上、できれば1万セット以上ほしい)
数理モデル
「個数が増えるほど金額も上がる」と「まとめ買いすると割引がある」という原理を表現できる関数を選択し、少ない学習データから係数を決定しました。
世の中の事象はすべてが数理モデル化できるわけではなく、数理モデルの粒度もいろいろです。数理モデル化は、背景にある原理を考慮し適切なモデルを構築できた場合に限りますが、少ない学習データから高い精度で事象を予測できる可能性を秘めています。またパラメータの説明や分析もしやすいです。今回のように原理がある程度想像できる場合には、思考停止で多項式近似やDeepでポン!するよりも、数理モデル化を行ったほうが良いでしょう。