やること
ZoomやWherebyといったオンライン会議ツールの法人契約に際して、「何部屋契約すれば足りるか分からない」という依頼がありました。例えば社員100人で毎週数百のミーティングが発生するのに5部屋契約ではきっと足りないでしょうし、逆に、社員が5人しかいないのに10部屋契約しても無駄になってしまいます。
近くにいた数学科出身に聞いてみたところ、「あー、面倒くさい(主に境界条件が)」と言われてしまったので、ここではモンテカルロ法でミーティング数と部屋数(チャンネル数)による足りた/足りないを計算してみます。なお、契約プランによってはアカウントの貸与・使い回しが禁止されていることもあるためご注意ください(個人プランを複数契約する等)。
モンテカルロ法とは
モンテカルロ法とは、ある値や確率が知りたいときに、コンピュータ内でサイコロを振りまくって実験的に求める方法です。
仮定
ミーティングは就業時間中のランダムな時間に入り、例えば
- Aさんミーティング:月曜日13:00~15:00
- Bさんミーティング:月曜日13:30~15:30
- Cさんミーティング:月曜日14:30~16:30
と入った場合、14:30~15:00の30分間は3並列で開催されているため、2チャンネル契約では足りず、3チャンネル以上の契約でセーフとなります。時間は30分単位で考えることにして、その他の条件は以下の通り。
- 月~金
- 午前:9:00~12:00
- 午後:13:00~17:00
- 1回のミーティング時間:2時間(準備・片付け時間含む)
- 週あたりミーティング発生数:0~19回で振る
- 契約するミーティングチャンネル数:0~9チャンネルで振る
この条件で1000週分シミュレーションを行い、ミーティング発生数と契約チャンネル数で振って「足りた確率=(足りた週/1000)」をプロットしてみます。
コード
パラメータ
import numpy as np
import numpy.random as nr
from copy import deepcopy
#パラメータ
unit_am = 6 #午前コマ数(30分単位)
unit_pm = 8 #午後コマ数(30分単位)
unit_mtg = 4 #ミーティングコマ数(30分単位)
max_mtg = 20 #発生し得る週あたり最大MTG数(1大きく指定)
max_channel = 10 #契約し得る最大MTGチャンネル数(1大きく指定)
#試行回数(週)
k = 1000モンテカルロ法
#午前または午後にMTGが投入される確率重み
weight_am = (unit_am - unit_mtg + 1) / ((unit_am - unit_mtg + 1) + (unit_pm - unit_mtg + 1))
print(weight_am)
weight_pm = (unit_pm - unit_mtg + 1) / ((unit_am - unit_mtg + 1) + (unit_pm - unit_mtg + 1))
print(weight_pm)
#答え配列
ans = np.zeros((max_channel, max_mtg))
#週あたりMTG数で繰り返し
for num_mtg in range(max_mtg):
#チャンネス数ごとの「足りました」カウント
count = np.zeros(max_channel, int)
#試行回数(週)繰り返し
for _ in range(k):
#午前と午後に入った回数カウント(コマ数, 曜日)
frame_am = np.zeros((unit_am, 5), int)
frame_pm = np.zeros((unit_pm, 5), int)
#MTG発生
for _ in range(num_mtg):
#午前か午後か
rand1 = nr.choice(['am', 'pm'], p=[weight_am, weight_pm])
#曜日
rand2 = nr.randint(5)
#該当の時間に入れる
if rand1 == 'am':
rand3 = nr.randint(unit_am - unit_mtg + 1)
frame_am[rand3:rand3+unit_mtg, rand2] += 1
else:
rand3 = nr.randint(unit_pm - unit_mtg + 1)
frame_pm[rand3:rand3+unit_mtg, rand2] += 1
#print(frame_am, frame_pm)
#チャンネル数が足りる部分をカウント+1
m = max(np.max(frame_am), np.max(frame_pm))
count[m:] += 1
#週数で割って「足りた」百分率とする
rate = count / k * 100
#print(rate)
#週あたりMTG数の列に記録
ans[:, num_mtg] = deepcopy(rate)0.375
0.625午前に入る確率が37.5%、午後は62.5%という意味です。境界条件のため、午前:午後=3時間:4時間の比のままにはなりません。
Excelに貼るためにカンマ区切りでコンソール出力します。
#表示
#print(ans)
for i in range(max_channel):
print(ans[i, 0], end='')
for j in range(1, max_mtg):
print(',', end='')
print(ans[i,j], end='')
print()100.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0
100.0,100.0,89.60000000000001,73.8,51.4,31.7,14.899999999999999,6.3,3.2,0.6,0.1,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0
100.0,100.0,100.0,98.8,96.89999999999999,88.9,85.8,77.8,63.9,56.10000000000001,40.6,29.9,20.7,15.0,7.199999999999999,4.3,1.7000000000000002,0.8999999999999999,0.5,0.1
100.0,100.0,100.0,100.0,100.0,99.4,98.3,97.0,94.6,92.4,87.9,82.39999999999999,75.2,67.4,57.99999999999999,53.5,43.3,39.2,26.900000000000002,22.0
100.0,100.0,100.0,100.0,100.0,100.0,100.0,99.9,99.6,99.7,98.6,96.89999999999999,96.2,94.5,90.4,88.8,82.89999999999999,80.80000000000001,73.7,69.5
100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,99.9,99.5,99.6,99.0,98.9,98.1,96.8,96.5,93.5,92.30000000000001
100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,99.9,99.9,100.0,100.0,99.5,99.2,98.9,98.1
100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,99.9,99.9,99.6
100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0
100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0,100.0結果
Excelに貼りました。
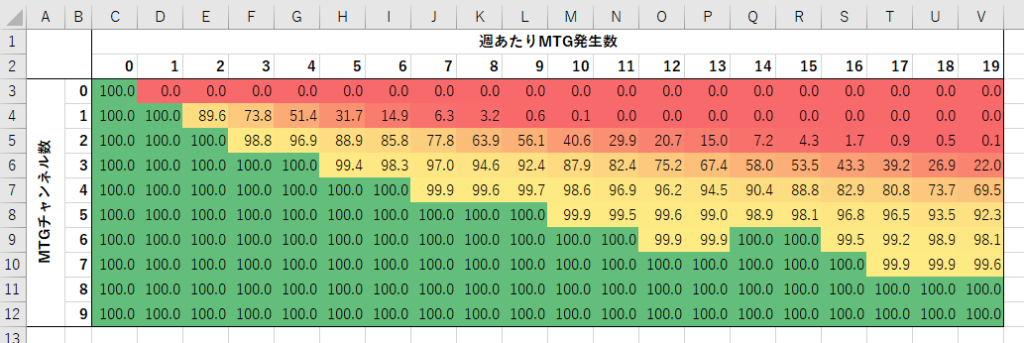
乱数の都合で途中がぐにゃっとしていますが、十分な情報が得られました。例えば週あたり10回のミーティングが発生する場合、4チャンネル契約で98.6%セーフ(1000週中986週は足りる)、5チャンネル契約で99.9%セーフです。あとは安全率や予算との相談で決められるでしょう。

