やること
「量子アニーリングをやっていて巡回セールスマン問題を解いたことがないとは何事だ?貴様にわかか?」と煽られました。泣きながら勉強しました。
今回は量子アニーリングで巡回セールスマン問題を解く方法を解説します。最短ルートで回る経路を見つける問題ですね。
おさらい
これまで、D-waveで問題を解くために「n個の量子ビットからm個を1にする」という条件設定を使っていました。
今回は新しく、「量子ビットaと量子ビットbが同時に1になったらペナルティを与える」という条件設定を使います。
実行環境
WinPython3.6をおすすめしています。
Google Colaboratoryが利用可能です。

量子アニーリングでどう解くのか
次のような4つの都市A, B, C, Dを最短で訪れる経路を求めることにします。各都市を結ぶ道の距離は分かっている必要があります。
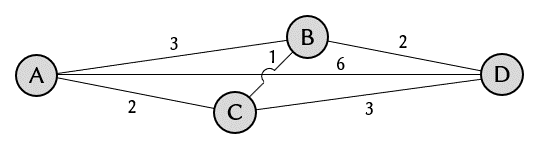
最短経路は、A-C-B-Dまたはその逆の2パターンあることが想像できます。
さっそく天から降ってきたアイデアですみませんが、次のような4×4のテーブルを作ります。とりあえず解の一例を記入しておきました。
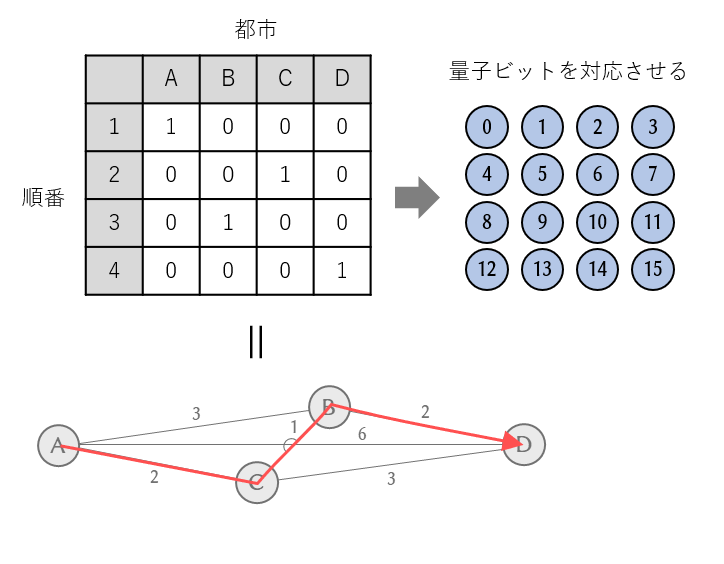
テーブルの各行、各列には1はそれぞれ一つしか入りません。記入済みの解は「1番目にA、2番目にC、3番目にB、4番目にD」という経路を意味しており、これが最短経路の一つです。このようなテーブルを用意することで、経路を0と1の並びで表現することができるのですね。テーブルの各セルを量子ビットに対応させて、16個の量子ビットのどれが0になるか、どれが1になるかを考えていきます。
準備
量子ビットを16個用意します。
import numpy as np
from pyqubo import Binary
from dwave.system.composites import EmbeddingComposite
from dwave.system.samplers import DWaveSampler
#量子ビットを用意する
q00 = Binary('q00')
q01 = Binary('q01')
q02 = Binary('q02')
q03 = Binary('q03')
q04 = Binary('q04')
q05 = Binary('q05')
q06 = Binary('q06')
q07 = Binary('q07')
q08 = Binary('q08')
q09 = Binary('q09')
q10 = Binary('q10')
q11 = Binary('q11')
q12 = Binary('q12')
q13 = Binary('q13')
q14 = Binary('q14')
q15 = Binary('q15')設定1(強い条件)
まず、問題を解く上で絶対に守ってほしい条件(強い条件)を設定していきます。ここでは「n個の量子ビットからm個を1にする」を使います。
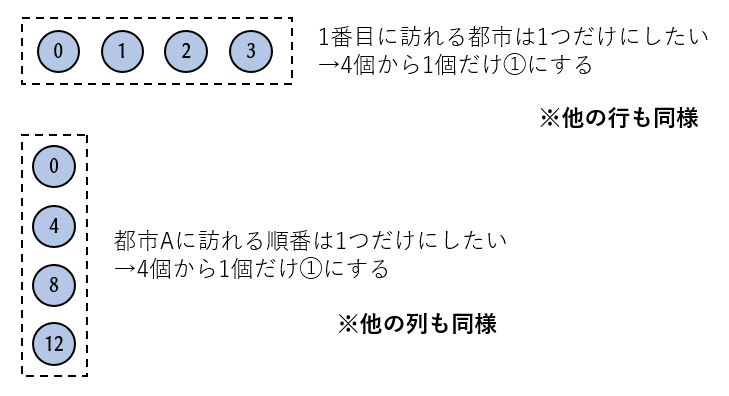
量子ビット [q0, q1, q2, q3] は1番目に訪れる都市を表しています。1番目に訪れる都市は一つしかあり得ないので、この中から1つだけが1になるという設定をします。他の3行も同様です。
また、量子ビット [q0, q4, q8, q12] は都市Aを訪れる順番(何番目か)を表しています。都市Aを訪れる順番は一つしかあり得ないので、やはりこの中から1つだけが1になるという設定をします。他の3列も同様です。
よって次のようにします。
#1番目に訪れる都市は1つだけにしたい、のやつ
H = 0
H += (q00 + q01 + q02 + q03 - 1)**2
H += (q04 + q05 + q06 + q07 - 1)**2
H += (q08 + q09 + q10 + q11 - 1)**2
H += (q12 + q13 + q14 + q15 - 1)**2
#都市Aに訪れる順番は1つだけにしたい、のやつ
H += (q00 + q04 + q08 + q12 - 1)**2
H += (q01 + q05 + q09 + q13 - 1)**2
H += (q02 + q06 + q10 + q14 - 1)**2
H += (q03 + q07 + q11 + q15 - 1)**2設定2(弱い条件)
次に、都市間の距離に基づいた設定をしていきます。次のように考えます。

赤矢印は、1番目の都市から2番目の都市Aに行く4パターンを表しています。左から2本目の矢印の説明を図中に書きました。1番目(B)→2番目(A)の移動になるということは、すなわち [q1, q4] の両方が同時に1になるということです。都市BとAの距離は3ですから、[q1, q4] が同時に1になった場合には3に比例したペナルティを与えることにしましょう。ここでは距離を10分の1にした0.3をペナルティとして与えます。
H += 0.3 * (q1 * q4)この式を見ると分かる通り、[q1, q4] が同時に1になるとエネルギーに0.3が追加されてしまいます。距離に比例したペナルティを設定することで、距離が長い道ほど採用しにくくなり、結果として最短経路が求まるという仕組みです。
ということで48個の式を追加しましょう。上の図から想像できるように、赤い矢印は48本あるので48式です。
#都市間の距離に比例したペナルティ
#1番目から2番目への移動について
H += 0.0 * (q00 * q04) #距離0なので
H += 0.3 * (q01 * q04) #距離3なので
H += 0.2 * (q02 * q04) #距離2なので
H += 0.6 * (q03 * q04) #距離6なので
H += 0.3 * (q00 * q05)
H += 0.0 * (q01 * q05)
H += 0.1 * (q02 * q05)
H += 0.2 * (q03 * q05)
H += 0.2 * (q00 * q06)
H += 0.1 * (q01 * q06)
H += 0.0 * (q02 * q06)
H += 0.3 * (q03 * q06)
H += 0.6 * (q00 * q07)
H += 0.2 * (q01 * q07)
H += 0.3 * (q02 * q07)
H += 0.0 * (q03 * q07)
#2番目から3番目への移動について
H += 0.0 * (q04 * q08)
H += 0.3 * (q05 * q08)
H += 0.2 * (q06 * q08)
H += 0.6 * (q07 * q08)
H += 0.3 * (q04 * q09)
H += 0.0 * (q05 * q09)
H += 0.1 * (q06 * q09)
H += 0.2 * (q07 * q09)
H += 0.2 * (q04 * q10)
H += 0.1 * (q05 * q10)
H += 0.0 * (q06 * q10)
H += 0.3 * (q07 * q10)
H += 0.6 * (q04 * q11)
H += 0.2 * (q05 * q11)
H += 0.3 * (q06 * q11)
H += 0.0 * (q07 * q11)
#3番目から4番目への移動について
H += 0.0 * (q08 * q12)
H += 0.3 * (q09 * q12)
H += 0.2 * (q10 * q12)
H += 0.6 * (q11 * q12)
H += 0.3 * (q08 * q13)
H += 0.0 * (q09 * q13)
H += 0.1 * (q10 * q13)
H += 0.2 * (q11 * q13)
H += 0.2 * (q08 * q14)
H += 0.1 * (q09 * q14)
H += 0.0 * (q10 * q14)
H += 0.3 * (q11 * q14)
H += 0.6 * (q08 * q15)
H += 0.2 * (q09 * q15)
H += 0.3 * (q10 * q15)
H += 0.0 * (q11 * q15)補足
補足ですが、「弱い条件」だけではすべての量子ビットが0になったり(どこも通らなければペナルティもないので)、ずっとAにいる、といった解が出てしまいます。しかし、「強い条件」によってそれは許されません。各行、各列は少なくとも一つずつ1にならないといけませんから、仕方なく一番ペナルティが小さい経路、すなわち最短経路が得られるということです。
さらに補足として、「4つの中から1つだけが1になる」という強い条件も、明示していませんが係数1のペナルティを与えています。式を見ての通り、1が2個あればペナルティ1、1が3個あればペナルティ4を与えます。強い条件のペナルティが1とか4といったオーダーですから、弱い条件はそれよりも小さいオーダーにするために距離を10分の1にして、0.0~0.6くらいのペナルティにしています。弱い条件は「全部は叶わず多少のペナルティが発生してしまう」ことを前提にしているから係数を小さいオーダーにするのです。係数が大きいと、弱い条件を満たすために強い条件を無視するという本末転倒なことが起きてしまいます。
アニーリング実行
あとはお決まりの実行です。サンプリング回数は1000にしました。
#コンパイル
model = H.compile()
qubo, offset = model.to_qubo()
print('qubo\n{}'.format(qubo))
#D-waveの設定
sampler = EmbeddingComposite(DWaveSampler(endpoint='https://cloud.dwavesys.com/sapi',
token='your_token', #あなたのAPIトークンを記入
solver='DW_2000Q_6')) #利用可能なソルバーを指定
#サンプリングしまくる
response = sampler.sample_qubo(qubo, num_reads=1000)
#レスポンスの確認
print('response')
for (sample, energy, occurrence, _) in response.data():
print('Sample:{} Energy:{} Occurrence:{}'.format(list(sample.values()), energy, occurrence))response
Sample:[1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1] Energy:-7.5 Occurrence:79
Sample:[0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0] Energy:-7.5 Occurrence:5
Sample:[1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1] Energy:-7.5 Occurrence:1
Sample:[0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0] Energy:-7.5 Occurrence:1
Sample:[1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1] Energy:-7.5 Occurrence:1
Sample:[1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1] Energy:-7.5 Occurrence:21
Sample:[0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0] Energy:-7.3 Occurrence:2
Sample:[0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0] Energy:-7.3 Occurrence:33
Sample:[0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0] Energy:-7.3 Occurrence:1
(以下略)重複した解がいくつも出てきましたが、エネルギーが最小の解は2パターンで、4×4に並べ直すと次の通り。
Sample:[1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1] Energy:-7.5 Occurrence:79
[[1 0 0 0]
[0 0 1 0]
[0 1 0 0]
[0 0 0 1]]
Sample:[0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0] Energy:-7.5 Occurrence:5
[[0 0 0 1]
[0 1 0 0]
[0 0 1 0]
[1 0 0 0]]A-C-B-Dとその逆の2パターンが得られました!
さいごに
量子アニーリングで重み付きの条件設定ができるようになりました。まだまだ活用例が広がると思うので、アイデアがあったら教えてください。