やること
前回に引き続き、HOBO対応の疑似アニーリングパッケージ「HOBOTAN」でペンシルパズルを解いていきましょう。
今回は「Takuzu(Binairo)」です。このパズル知ってますか?
※この記事はQUBOアニーリングの基礎講座を履修済みであることを前提としています。
TYTANについて
前身となる「TYTAN」はOSSの疑似量子アニーリングパッケージです。
日本量子コンピューティング協会が運営しているチュートリアル教材はこちら。
私のオンライン講義でよければこちらから見れます。
discordコミュニティもあるので気軽に質問できます。
HOBOTANについて
それを元にしてできたのが「HOBOTAN」。使い方はTYTANとほとんど同じです。分からないことがあれば何でも聞いてください。
Takuzuとは
このパズルにはいくつか別名があります。
- タクズ(Takuzu)
- ビナイロ(Binairo)
- まるばつロジック
Puzzle Team さんはBinairoと呼んでいます。1問お借りします。
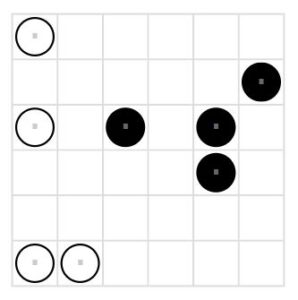
ルールは、盤面を黒と白の玉で埋めるのですが、各行、各列とも白と黒が同数(3個ずつ)入ります。また、直線に3つ同じ色が並んではいけません。さらに、まったく同じ配列の行が2つ以上あってはいけません(列も同様)。
答えはこちらです。

コンセプティスパズル さんでも遊べます(こちらはまるばつロジックという名前ですね)。
定式化
この手の二値タイプのパズルはQUBO/HOBOと相性が良いですね。
黒を0、白を1としておきます。あらかじめ決まっているマスの制約と、各行・各列とも3個だけ1にする制約を設定します。
「直線に3つ同じ色が並んではいけない」はHOBOTANのチュートリアルにある「教室の席にできるだけ多くの生徒を座らせる(ただし縦・横に3席連続で座ってはいけない)」と同じ設定ですね。また出ました。これが3次の項なのでHOBOになります。
from hobotan import *
import numpy as np
import matplotlib.pyplot as plt
#問題(空マスは5にした)
question = [[1,5,5,5,5,5],
[5,5,5,5,5,0],
[1,5,0,5,0,5],
[5,5,5,5,0,5],
[5,5,5,5,5,5],
[1,1,5,5,5,5]]
#量子ビットの用意
q = symbols_list([6, 6], 'q{}_{}')
#式を用意
Hconst = 0
#問題を反映
for i in range(6):
for j in range(6):
if question[i][j] != 5:
Hconst += (q[i, j] - question[i][j])**2
#よこ方向の白は3個
for i in range(6):
Hconst += (np.sum(q[i, :]) - 3)**2
#たて方向の白は3個
for j in range(6):
Hconst += (np.sum(q[:, j]) - 3)**2
#直線の3マスが連続で1になったら臨時ペナルティ
for i in range(6):
for j in range(6 - 3 + 1):
Hconst += np.prod(q[i, j:j+3])
for j in range(6):
for i in range(6 - 3 + 1):
Hconst += np.prod(q[i:i+3, j])
#直線の3マスが連続で0になったら臨時ペナルティ
for i in range(6):
for j in range(6 - 3 + 1):
Hconst += np.prod((1 - q[i, j:j+3]))
for j in range(6):
for i in range(6 - 3 + 1):
Hconst += np.prod((1 - q[i:i+3, j]))
#式の合体
H = Hconst
#HOBOテンソルにコンパイル
hobo, offset = Compile(H).get_hobo()
print(f'offset\n{offset}')
#サンプラー選択
solver = sampler.MIKASAmpler()
#サンプリング
result = solver.run(hobo, shots=1000, T_num=10000)
#上位3件
for r in result[:3]:
print(f'Energy {r[1]}, Occurrence {r[2]}')
#さくっと配列に
arr, subs = Auto_array(r[0]).get_ndarray('q{}_{}')
#さくっと画像に
img, subs = Auto_array(r[0]).get_image('q{}_{}')
plt.figure(figsize=(3, 3))
plt.imshow(img)
plt.show()tensor order = 2
----- compile -----
MODE: GPU
DEVICE: cuda:0
-------------------
offset
160.0
===== sampler =====
MODE: GPU
DEVICE: cuda:0
===================
.......... 1000/10000 min=-156.0 mean=-149.4350128173828
.......... 2000/10000 min=-156.0 mean=-150.55599975585938
.......... 3000/10000 min=-158.0 mean=-151.4910125732422
(中略)
.......... 8000/10000 min=-160.0 mean=-156.65200805664062
.......... 9000/10000 min=-160.0 mean=-156.7930145263672
.......... 10000/10000 min=-160.0 mean=-156.9390106201172
Energy -160.0, Occurrence 6
(画像)
Energy -160.0, Occurrence 3
(画像)
Energy -159.0, Occurrence 1
(画像)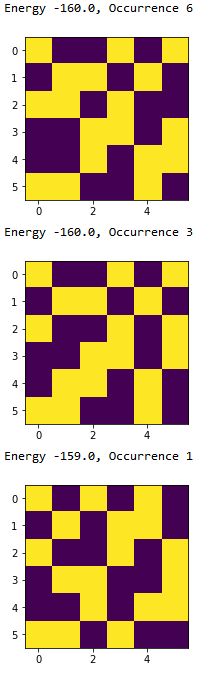

オフセットが160、解のエネルギーが-160(理想的)のものが2種類出ました。正解と見比べてみてどうでしょうか?1番目は正しいですが、2番目は不正解です。
2番目の解は同じ配列があちこちに現れてしまっています。
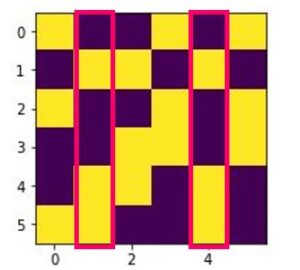
エネルギーが理想的だったにもかかわらず正しくないということは、制約条件が間違っていた(足りなかった)ということですね。やはり「同じ配列の行が2つ以上あってはいけない(列も同様)」の設定が必要です。
配列の一致の検出
ということで「マスが6組とも一致したら臨時ペナルティ」を設定したいです。
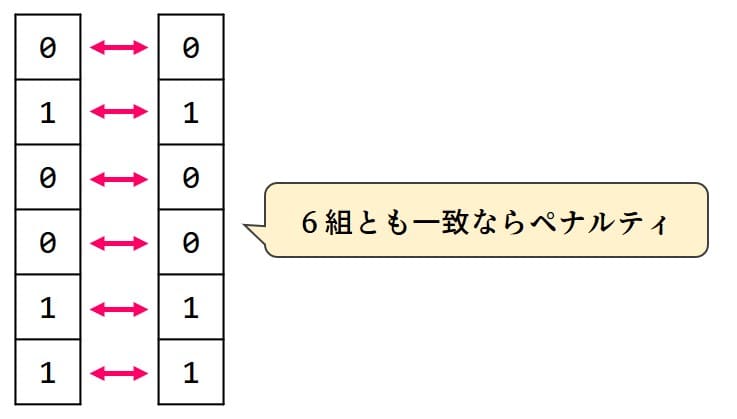
思いっきり簡単にして「マスが2組とも一致したらペナルティ」を考えてみましょう。
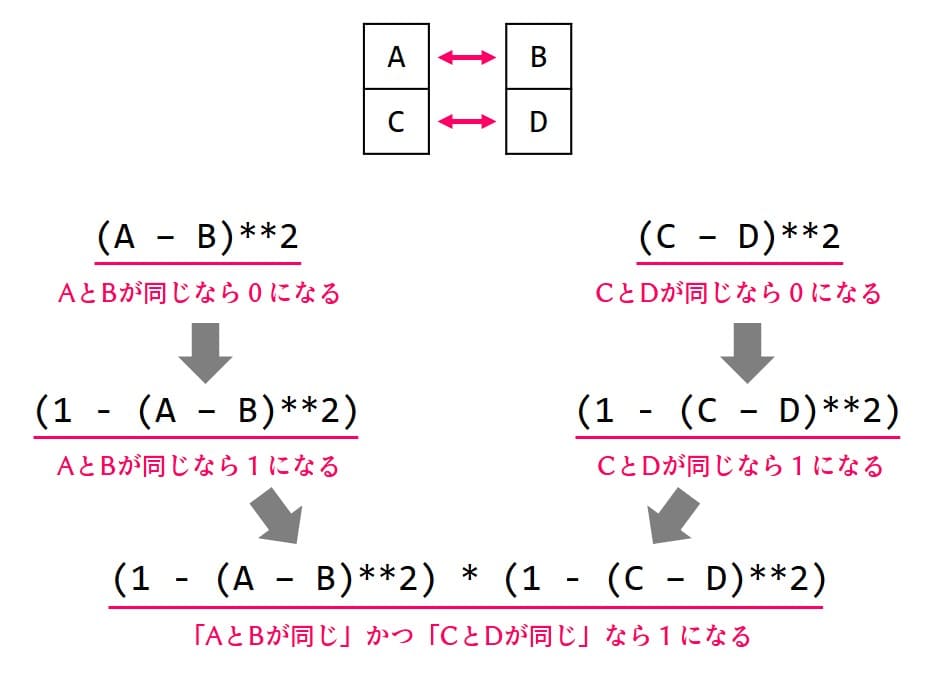
AとBの一致は (A – B)^2 で判定できます。[0, 0] or [1, 1] なら0に、[0, 1] or [1, 0] なら1になります。一致したときに1になってほしいので、この式の否定(=0/1を逆転させる)で (1 – (A – B)^2) となります(→量子アニーリング(QUBO)で複数の数字を均等に2組に分ける)。これでAとBの一致判定ができました。同じことをCとDでも行い、それらをかけ算(=同時に1になったら)すれば「2組とも一致したら1」の出来上がりです。
ところで、(1 – (A – B)^2) × (1 – (C – D)^2) の次数はいくつか?つまり、最大で何個の量子ビットのかけ算になっているかです。展開すると4次だと分かります。
実際は「6組とも一致したら臨時ペナルティ」なので・・・
(1 – ( )^2) × (1 – ( )^2) × (1 – ( )^2) × (1 – ( )^2) × (1 – ( )^2) × (1 – ( )^2)
展開すると12次の式になります。。圧倒的HOBO感!
6列あってどの列も重複してはならないなので、(列目でいうところの)1-2, 1-3, 1-4, 1-5, 1-6, 2-3, 2-4, 2-5, 2-6, 3-4, 3-5, 3-6, 4-5, 4-6, 5-6 の15通りの一致ペナルティを設定します。6C2のコンビネーションで次のように設定できます。
from itertools import combinations
#よこ配列が重複しない
for a, b in combinations(range(6), 2):
Hconst += (1 - (q[a, 0]-q[b, 0])**2) * (1 - (q[a, 1]-q[b, 1])**2) * (1 - (q[a, 2]-q[b, 2])**2)\
* (1 - (q[a, 3]-q[b, 3])**2) * (1 - (q[a, 4]-q[b, 4])**2) * (1 - (q[a, 5]-q[b, 5])**2)
#たて配列が重複しない
for a, b in combinations(range(6), 2):
Hconst += (1 - (q[0, a]-q[0, b])**2) * (1 - (q[1, a]-q[1, b])**2) * (1 - (q[2, a]-q[2, b])**2)\
* (1 - (q[3, a]-q[3, b])**2) * (1 - (q[4, a]-q[4, b])**2) * (1 - (q[5, a]-q[5, b])**2)tensor order = 12
----- compile -----
MODE: GPU
DEVICE: cuda:0
-------------------
offset
190.0
===== sampler =====
MODE: GPU
DEVICE: cuda:0
===================
.......... 1000/10000 min=-184.0 mean=-179.20901489257812
.......... 2000/10000 min=-186.0 mean=-180.26100158691406
.......... 3000/10000 min=-186.0 mean=-181.1070098876953
(中略)
.......... 8000/10000 min=-190.0 mean=-186.239013671875
.......... 9000/10000 min=-190.0 mean=-186.4110107421875
.......... 10000/10000 min=-190.0 mean=-186.58700561523438
Energy -190.0, Occurrence 7
(画像)
Energy -189.0, Occurrence 3
(画像)
Energy -189.0, Occurrence 1
(画像)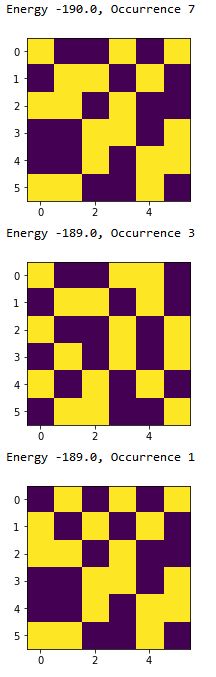

今度はどうでしょうか?理想的なエネルギーの解が一つだけ出ました。見事に正解です。
ちなみに実行時間はそれなりのGPUでも10分以上かかります。
余談(計算速度の話)
2025年1月現在、TYTANパッケージとHOBOTANパッケージはどちらもHOBOに対応しています。どちらで解いても構いません。
しかし、TYTANが通常のテンソルを使うのに対し、HOBOTANは疎テンソルでデータを扱うように改良されています。TYTANで量子ビット数=5のHOBOをコンパイルすると5次テンソルなので55の要素をもつテンソルになりメモリに乗り切りません(乗るかもしれんけど)。一方のHOBOTANはコンパイルが通ります(式が多いとアニーリング作業は遅いですが)。
ということで(およそ)5次以上のHOBOを扱うならHOBOTANがいいです。
おわりに
なお、Takuzuには10×10や20×20サイズの問題もあります。40次のテンソルは、、無理ですね ( ˘ω˘ )アーヤメヤメ


