AI要約
量子ゲートでピクセルアートを作るシリーズの第1弾。3×3サイズの白黒画像を量子回路で生成する挑戦。量子状態の操作とサンプリングの仕組みを活かして、量子コンピュータによるアート制作に取り組みました。
はじめに
2025年3月某日、blueqatさんが珍妙なゲームを(何の前触れもなく)公開しました。こちらの動画の1:20付近からご覧ください。
今回から、量子ゲート計算でこのようなピクセルアートを生成する方法を学んでいきます。
前提
すみませんが量子ゲートでNOT, AND, OR, XORを作る話やQiskitの使い方は過去の記事を履修してください。

はじめに2
8×8サイズのネコは64マスでできているので、ぶっちゃけ64量子ビット分の五線譜を書いて一つ一つ0か1を定義してやれば絵そのものは簡単に生成できます。しかしそれではスケールアップが困難です。16×16サイズだと256量子ビット。補助量子ビットも加えると軽く1000量子ビットを超えてきます。いくら量子ビットがあっても足りません。
動画では、64マスのネコを「たった6量子ビットで描画している」と言っています。これは26=64からきています。どういうことかというと、量子計算から出てきた6量子ビットを10進数で解釈して、対応するN番目のマスを塗ります。こういうデコーダを介して描画するのです。これは、量子ビットを節約することの代償として、1回の計算で塗られるのが1マスだけになることを意味します。単発計算を繰り返すことであちこちのマスが塗られていき、統計的に見ると絵が出来上がるのだという。このようにサンプリングの考え方を活用するのは量子コンピュータっぽさがありますし、学習するモチベーションも上がりますね。
よって、これから取り組んでいくのですが、「マス目の総数に対応した量子ビットの用意をしてはいけない」という制限を付けます。つまり、8×8サイズのイラストを作るときに64個の何かを並べてはならず、6ビットの0/1の組み合わせとして64通りを表現する必要があるのです。
3×3サイズの問題
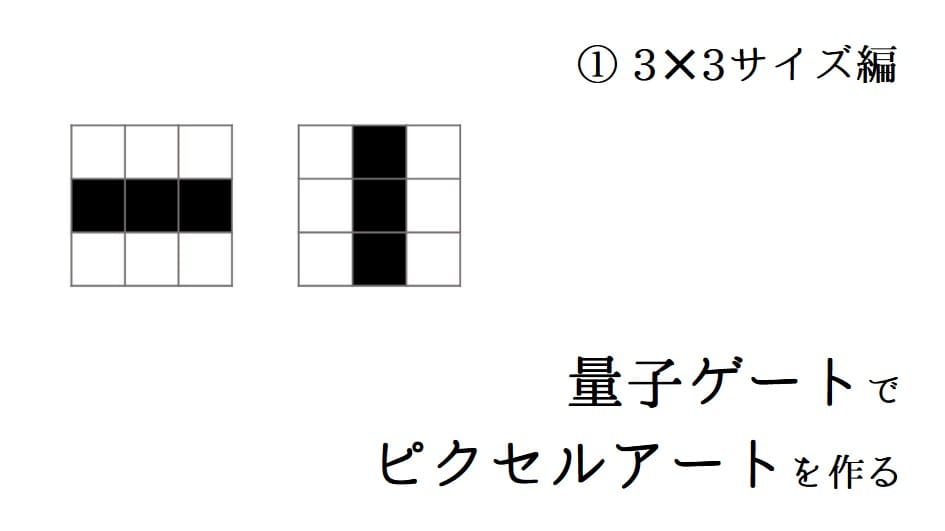
早速、小さな問題として3×3サイズのイラストを作ってみます。こちらが全体構成です。
単一の絵を生成するだけでもいいのですが、ネコジャンプが2パターン生成なのでこちらもそうしてみます。ちなみにこのイラストはライフゲームでもっともよく見られる振動子「ブリンカー」です。周期が2なので2パターンの生成にちょうどいいかと思ってのチョイス。
上の図で重要なことは、量子ゲート計算の出力は3ビットであり、8マスの中から対応する1マスが塗られます。これを繰り返すことで入力が0なら横一文字。入力が1なら縦一文字のイラストが見えてきます。
では、「いい感じのゲートたち」の中身を詳しく見てみます。
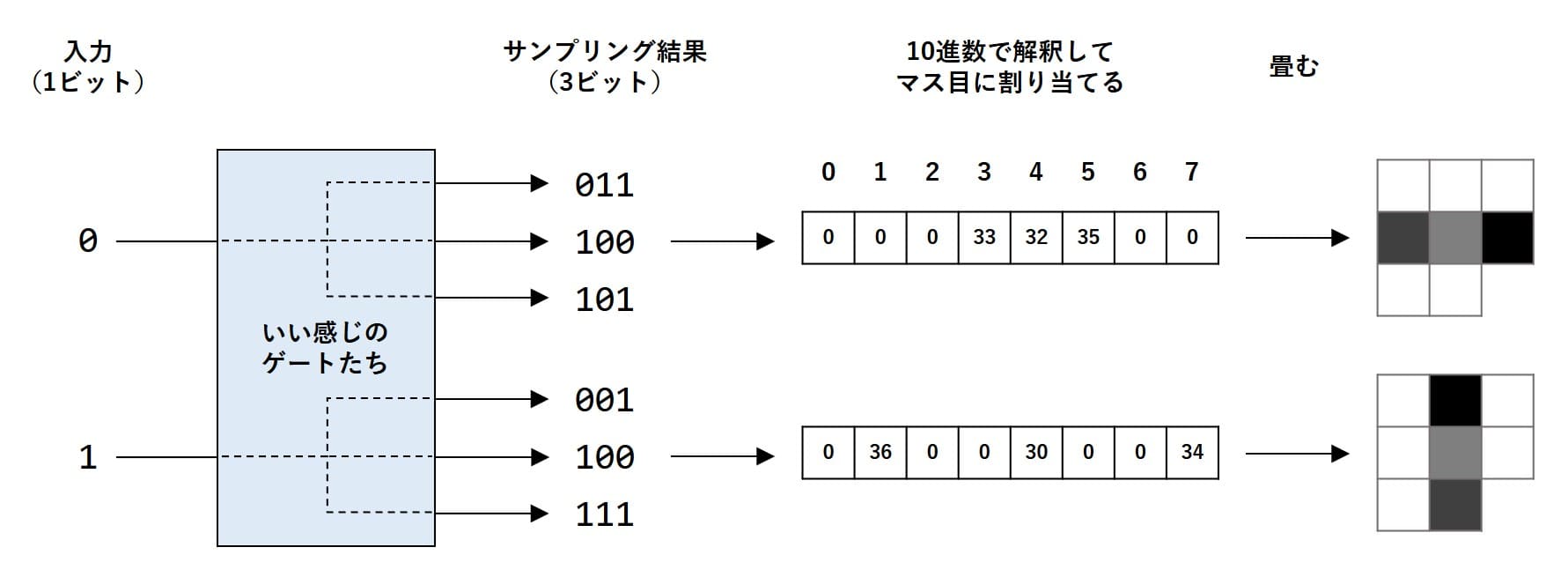
中では量子計算がもたらす確率分布を考えています。そう、量子コンピュータは確率分布を操作するマシンであるというのが、古典コンピュータと決定的に違うポイントなのです。入力が0なら [011, 100, 101] の3通りだけが出力されます。どれが出るかはHゲートを活用してランダムにします。入力が1ならまた違った確率分布に基づいた結果を出します。
もっと詳しく中身を見てみましょう。
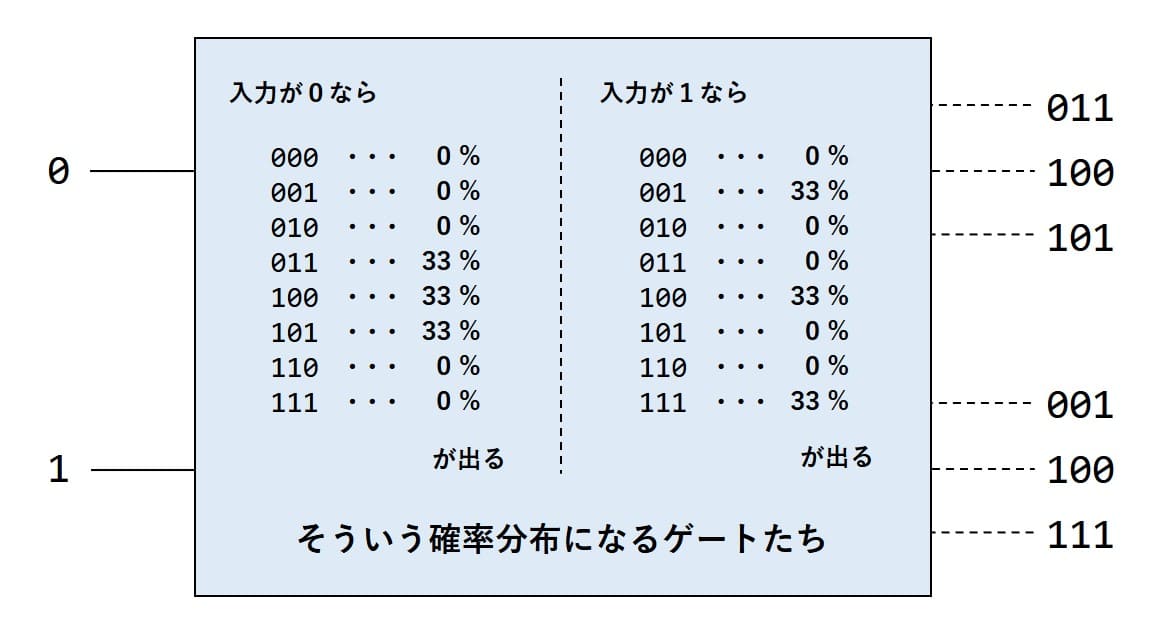
入力は1ビットと書いていましたが、実際には乱数を生むためのビットも入力と言えるかもしれません。2ビットを各々Hゲートに通すことで [00, 01, 10, 11] の4通りの乱数を生成します。ここからが難しいところなのですが、この2ビットの乱数を用いて(入力が0の場合)[011, 100, 101] の3通りだけが出るような論理合成を行います。(は?)
ブリンカーの論理合成
そろそろついてこれない。
まず、乱数は4通りで、生成したい出力は3通りです。塗りたいマスが3個だからそれと同じか少し多い4通りの乱数を生むために乱数ビットを2個にしたわけです。
ここで、4通りの乱数をいい感じに3通りの出力に割り振ります。以下のように割り当てました。
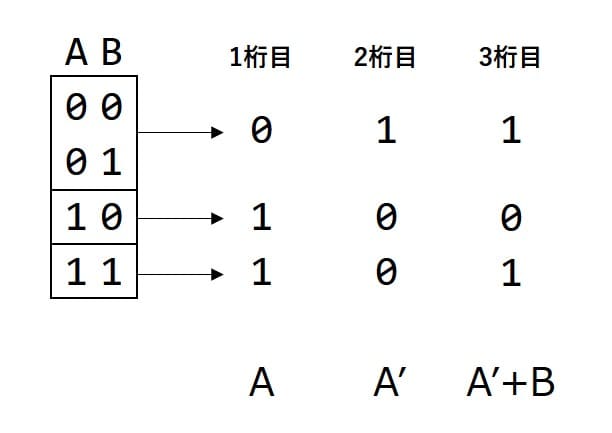
乱数ビットをA, Bとして、各桁について目的の結果が得られるような論理式をひねり出します。
1桁目 = A
2桁目 = A' ※(not A)
3桁目 = A' + B ※{(not A) or B}同様に、入力が1のときも考えます。
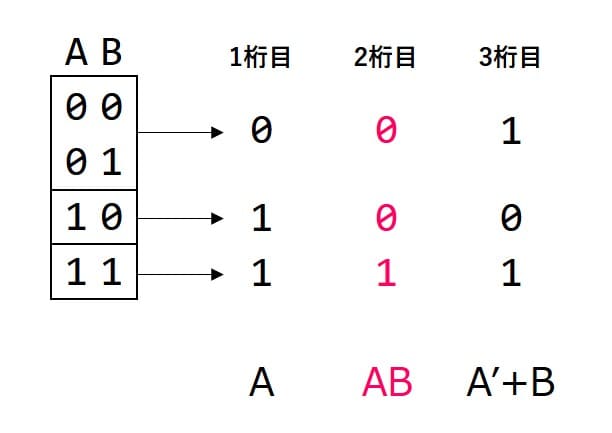
1桁目 = A
2桁目 = AB ※(A and B)
3桁目 = A' + B ※再利用赤字のところだけが新規で、他は入力=0のときのが再利用できます。
コード
コードで確認します。CXゲートでコピペ、CCXゲートで条件付きコピペのようなことができることに注意してください。0番目の量子ビットにXゲートをかけるかどうかで入力を切り替えてください。
import numpy as np
import matplotlib.pyplot as plt
from qiskit import QuantumCircuit
from qiskit_aer import AerSimulator
def NOT(i, j):
global qc
"""
(NOT i) -> j
"""
qc.cx(i, j)
qc.x(j)
def AND(i, j, k):
global qc
"""
(i AND j) -> k
"""
qc.ccx(i, j, k)
def XOR(i, j, k):
global qc
"""
(i XOR j) -> k
"""
qc.cx(i, k)
qc.cx(j, k)
def OR(i, j, k):
global qc
"""
(i OR j) -> k
"""
qc.x(i)
qc.x(j)
qc.ccx(i, j, k)
qc.x(i)
qc.x(j)
qc.x(k)
#初期化
qc = QuantumCircuit(15)
#入力の1ビット
# qc.x(0) # ここを切り替える
#入力のNOT
NOT(0, 1)
#2ビット(4通り)の乱数を作る
qc.h(2) # A
qc.h(3) # B
#便利のため、各NOTを用意
NOT(2, 4) # A'
NOT(3, 5) # B'
#入力=0のときの出力の3ビット
qc.cx(2, 6) # A
qc.cx(4, 7) # A'
OR(4, 3, 8) # A'+B
#入力=1のときの出力の3ビット
qc.cx(2, 9) # A
AND(2, 3, 10) # AB
qc.cx(8, 11) # A'+B
#入力に応じて出力を切り替える
qc.ccx(1, 6, 12) # 1桁目
qc.ccx(1, 7, 13) # 2桁目
qc.ccx(1, 8, 14) # 3桁目
qc.ccx(0, 9, 12) # 1桁目
qc.ccx(0, 10, 13) # 2桁目
qc.ccx(0, 11, 14) # 3桁目
#サンプリング
qc.measure_all()
backend = AerSimulator(method='matrix_product_state')
result = backend.run(qc, shots=500).result().get_counts()
#解の統計
pos = (0, 2, 3, 12, 13, 14)
for i in range(2):
for j in range(2):
for r in result:
# print(r)
sel = ''.join(r[::-1][p] for p in pos)
if f'{i}{j}' == sel[1:3]:
print(f'{sel[0]} | {sel[1:3]} | {sel[3:]} | {result[r]}/500')入力=0のときの結果
0 | 00 | 011 | 112/500
0 | 01 | 011 | 134/500
0 | 10 | 100 | 137/500
0 | 11 | 101 | 117/500入力=1のときの結果
1 | 00 | 001 | 129/500
1 | 01 | 001 | 120/500
1 | 10 | 100 | 139/500
1 | 11 | 111 | 112/500結果は左から「入力」「乱数」「出力」「ヒット回数」です。どうでしょうか。設計通りの確率分布で2パターンの塗り方が生成できました。なお、4通りの一様乱数に3通りの状態を割り当てたため等確率ではありません。入力が0の場合、[011, 100, 101] = [50%, 25%, 25%] の確率分布となっています。
量子譜はこちら。
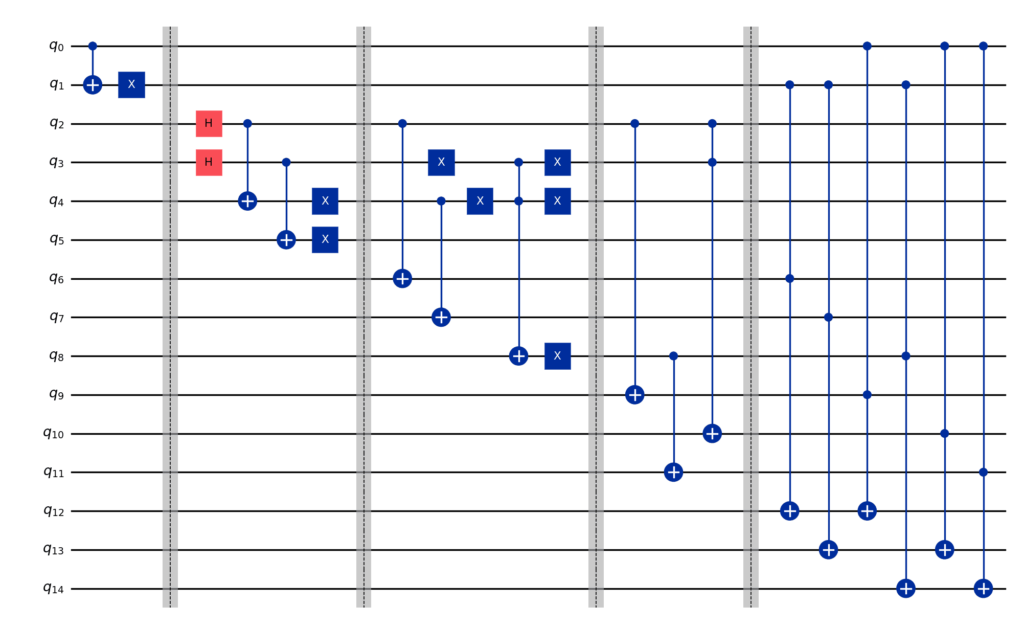
イラスト生成
設計が大丈夫そうなので、サンプリングしながらイラスト化してみましょう。過去に塗ったマスの色を0.9倍に減衰させています(訂正:1.1で割ってます)。
#サンプリングしながらピクセルを点灯
pos = (12, 13, 14)
box = np.zeros(9, 'uint8')
for i in range(50):
qc.measure_all()
backend = AerSimulator(method='matrix_product_state')
result = backend.run(qc, shots=1).result().get_counts()
r = list(result)[0]
sel = ''.join(r[::-1][p] for p in pos)
#10進数ワンホットに戻す
box = box // 1.1 # 過去の色を減衰させる
idx = int(sel[0])*2**2 + int(sel[1])*2**1 + int(sel[2])*2**0
box[idx] = 255
#表示
img = box.reshape(3, 3)
plt.imshow(img, vmin=0, vmax=255)
plt.title(sel)
plt.show()
plt.close()入力=0
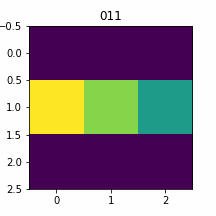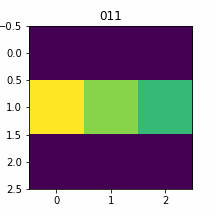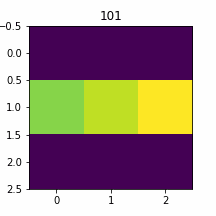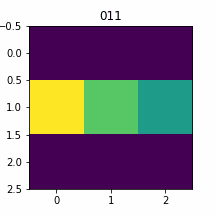
入力=1
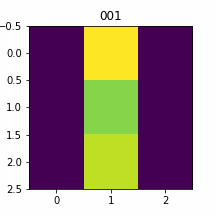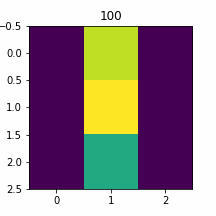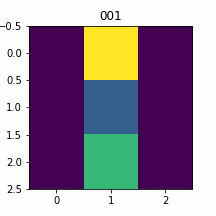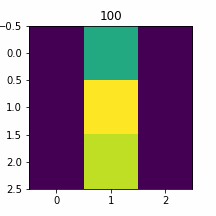
できましたね!
おわりに
いや、うん、いつものことですが我々はどこへ向かっているのか?みんな何処へ行った?見送られることもなく!
次回は4×4サイズのイラスト生成します。