量子ゲートでピクセルアートを作る（②4×4サイズ編）

AI要約
はじめに
４×４サイズの問題
ヒキガエルの論理合成
コード
イラスト生成
おわりに

AI要約

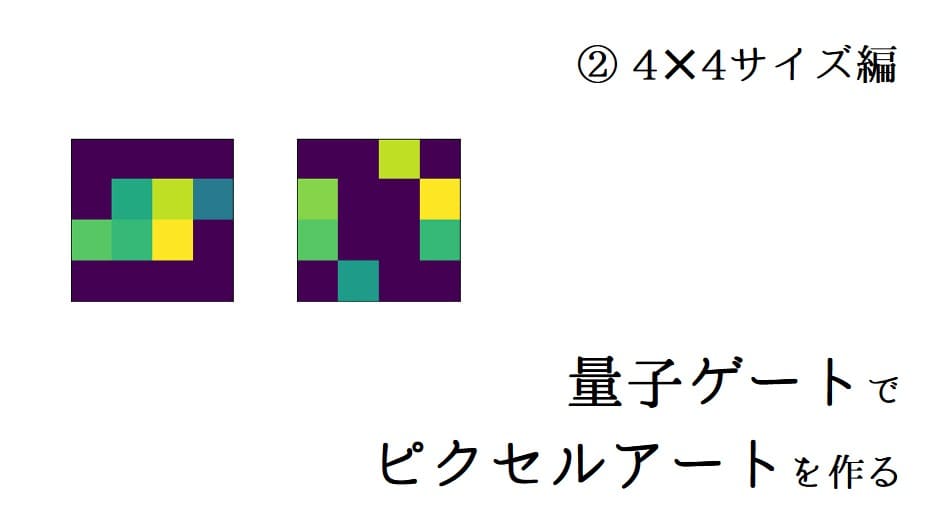
3×3に続き、4×4のピクセルアートを量子回路で描く方法を解説。量子ビットの割り当てやゲート操作を通じて、より複雑な量子アートの表現に挑戦しています。

はじめに

いいものを買ってきた。ほ～れ～

if文で書いたほうが早いんじゃないか？

びゃあ゛ぁぁうまひぃいぃぃ゛ぃぃぃい！！！やっぱり量子コンピュータで生成したイラストは一味違いますよ～！！

　　終
制作・著作
━━━━━
　ⓃⒽⓀ

ということで、前回は量子ゲート計算でライフゲームの「ブリンカー」を生成しました。

今回は少し拡張して４×４サイズのイラストを生成してみます。

４×４サイズの問題

またしてもライフゲームの振動子「ヒキガエル」です。いったいどこがヒキガエルなのか。

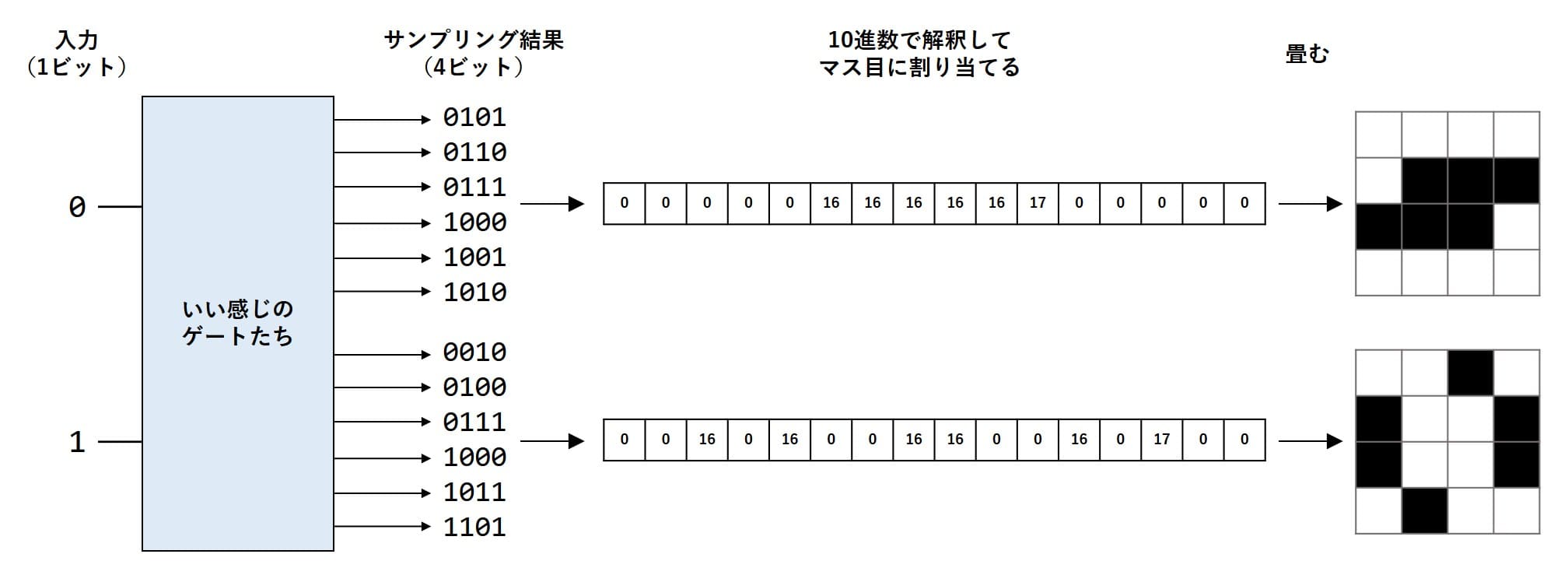
16マスあるのでちょっと大変そうですね。実際大変です。量子パートの出力は４ビットです。

「いい感じのゲートたち」の中身を詳しく見てみます。

おいおい、こんなのできるのか？正直しんどいです。量子コンピュータが確率分布を操作するマシンであることを改めて痛感します。入力が０なら [0101, 0110, 0111, 1000, 1001, 1010] の６通りだけが出力されるようにします。

また、塗るマスが６個なので乱数は３ビット必要です。

ヒキガエルの論理合成

乱数は８通りで、生成したい出力は６通り。

いろいろな振り分け方がありますが、心眼を使って効率が良さそうな割り当てを決めます。ズバリ以下の通り。

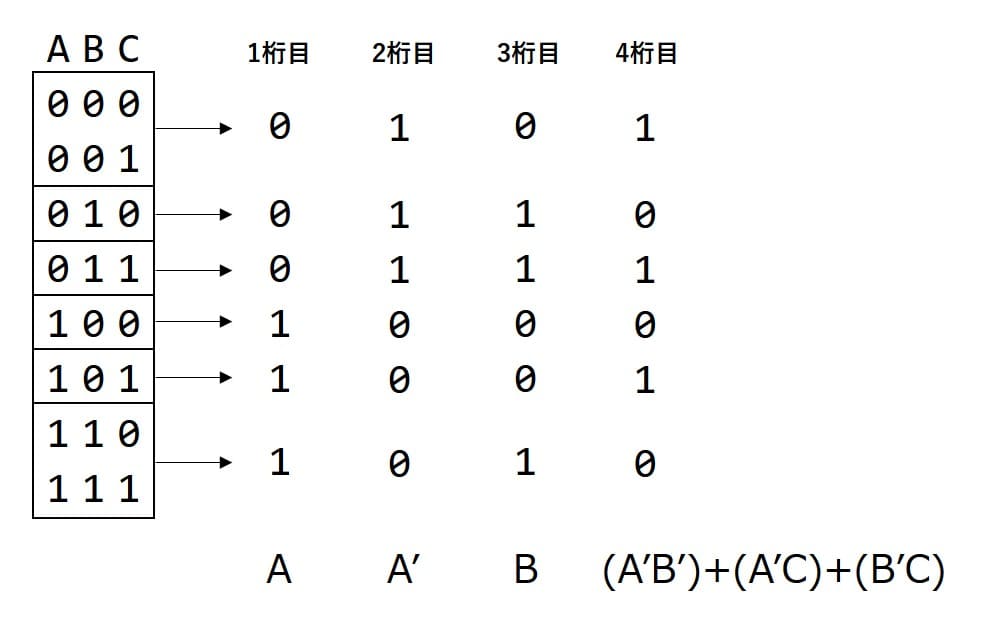
乱数ビットをA, B, Cとして、なんと１～３桁目まで「そのまんまやんけ！」です。４桁目はどうにもならないので論理式をひねり出します。

1桁目 ＝ A

2桁目 ＝ A'

3桁目 ＝ B

4桁目 ＝ A'B' + A'C + B'C

同様に、入力が１のときも考えます。

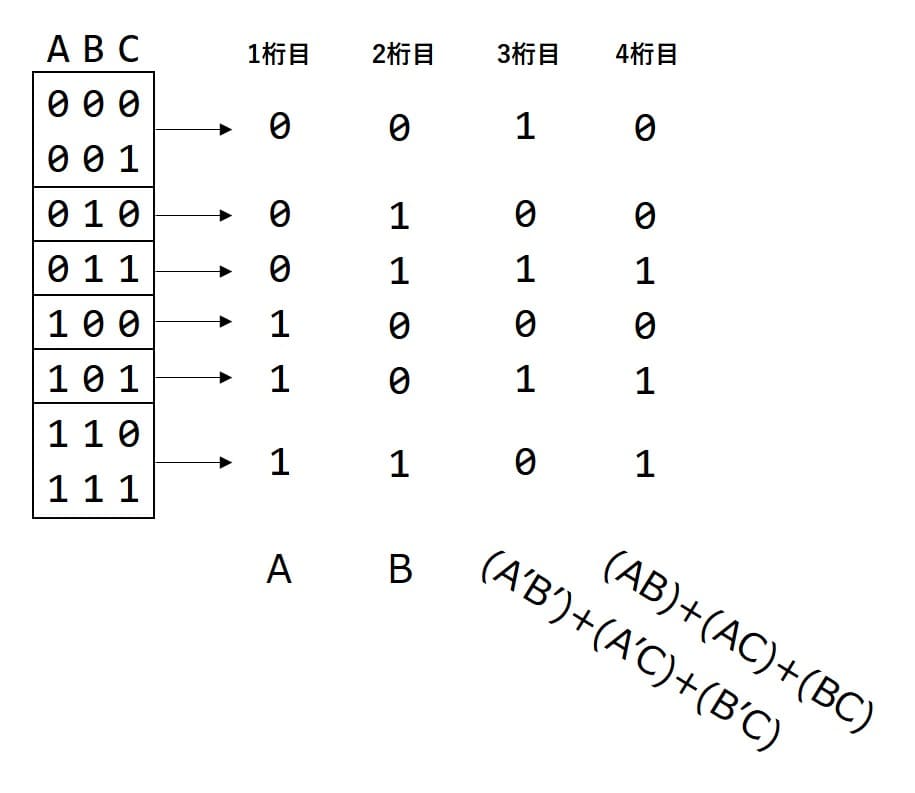
1桁目 ＝ A

2桁目 ＝ B

3桁目 ＝ A'B' + A'C + B'C　※再利用

4桁目 ＝ AB + AC + BC

３桁目はさっきの再利用です。

コード

コードで確認します。０番目の量子ビットにXゲートをかけるかどうかで入力を切り替えてください。

import numpy as np
import matplotlib.pyplot as plt
from qiskit import QuantumCircuit
from qiskit_aer import AerSimulator


def NOT(i, j):
    global qc
    """
    (NOT i) -> j
    """
    qc.cx(i, j)
    qc.x(j)

def AND(i, j, k):
    global qc
    """
    (i AND j) -> k
    """
    qc.ccx(i, j, k)

def XOR(i, j, k):
    global qc
    """
    (i XOR j) -> k
    """
    qc.cx(i, k)
    qc.cx(j, k)

def OR(i, j, k):
    global qc
    """
    (i OR j) -> k
    """
    qc.x(i)
    qc.x(j)
    qc.ccx(i, j, k)
    qc.x(i)
    qc.x(j)
    qc.x(k)


#初期化
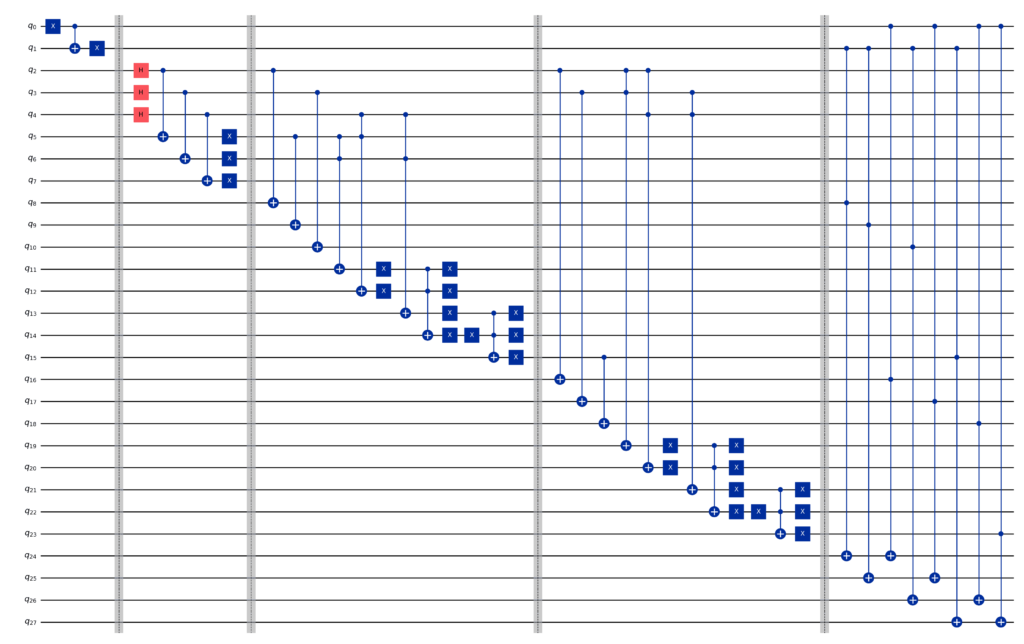
qc = QuantumCircuit(28)

#入力の1ビット
# qc.x(0) # ここを切り替える

#入力のNOT
NOT(0, 1)

#3ビット（8通り）の乱数を作る
qc.h(2) # A
qc.h(3) # B
qc.h(4) # C

#便利のため、各NOTを用意
NOT(2, 5) # A'
NOT(3, 6) # B'
NOT(4, 7) # C'

#入力=0のときの出力の3ビット
qc.cx(2, 8) # A

qc.cx(5, 9) # A'

qc.cx(3, 10) # B

AND(5, 6, 11) # A'B'
AND(5, 4, 12) # A'C
AND(6, 4, 13) # B'C
OR(11, 12, 14) # A'B' + A'C
OR(14, 13, 15) # A'B' + A'C + B'C

#入力=1のときの出力の3ビット
qc.cx(2, 16) # A

qc.cx(3, 17) # B

qc.cx(15, 18) # A'B' + A'C + B'C

AND(2, 3, 19) # AB
AND(2, 4, 20) # AC
AND(3, 4, 21) # BC
OR(19, 20, 22) # AB + AC
OR(22, 21, 23) # AB + AC + BC

#入力に応じて出力を切り替える
qc.ccx(1, 8, 24) # 1桁目
qc.ccx(1, 9, 25) # 2桁目
qc.ccx(1, 10, 26) # 3桁目
qc.ccx(1, 15, 27) # 4桁目

qc.ccx(0, 16, 24) # 1桁目
qc.ccx(0, 17, 25) # 2桁目
qc.ccx(0, 18, 26) # 3桁目
qc.ccx(0, 23, 27) # 4桁目


#サンプリング
qc.measure_all()
backend = AerSimulator(method='matrix_product_state')
result = backend.run(qc, shots=500).result().get_counts()

#解の統計
pos = (0, 2, 3, 4, 24, 25, 26, 27)
for i in range(2):
    for j in range(2):
        for k in range(2):
            for r in result:
                # print(r)
                sel = ''.join(r[::-1][p] for p in pos)
                if f'{i}{j}{k}' == sel[1:4]:
                    print(f'{sel[0]} | {sel[1:4]} | {sel[4:]} | {result[r]}/500')

入力＝０のときの結果

0 | 000 | 0101 | 42/500
0 | 001 | 0101 | 56/500
0 | 010 | 0110 | 60/500
0 | 011 | 0111 | 62/500
0 | 100 | 1000 | 72/500
0 | 101 | 1001 | 79/500
0 | 110 | 1010 | 64/500
0 | 111 | 1010 | 65/500

入力＝１のときの結果

1 | 000 | 0010 | 48/500
1 | 001 | 0010 | 73/500
1 | 010 | 0100 | 71/500
1 | 011 | 0111 | 52/500
1 | 100 | 1000 | 65/500
1 | 101 | 1011 | 80/500
1 | 110 | 1101 | 52/500
1 | 111 | 1101 | 59/500

結果は左から「入力」「乱数」「出力」「ヒット回数」です。多分合ってる！（ヤケクソになってきている）

量子譜はこちら。

イラスト生成

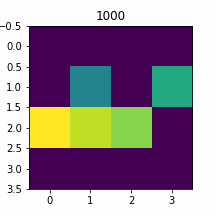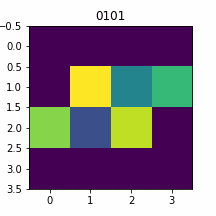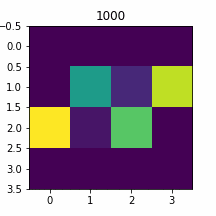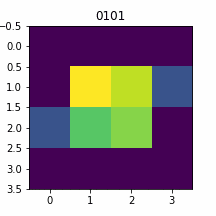
サンプリングしながらイラスト化します。

#サンプリングしながらピクセルを点灯
pos = (24, 25, 26, 27)
box = np.zeros(16, 'uint8')
for i in range(50):
    qc.measure_all()
    backend = AerSimulator(method='matrix_product_state')
    result = backend.run(qc, shots=1).result().get_counts()
    r = list(result)[0]
    sel = ''.join(r[::-1][p] for p in pos)
    
    #10進数ワンホットに戻す
    box = box // 1.1 # 過去の色を減衰させる
    idx = int(sel[0])*2**3 + int(sel[1])*2**2 + int(sel[2])*2**1 + int(sel[3])*2**0
    box[idx] = 255
    
    #表示
    img = box.reshape(4, 4)
    plt.imshow(img, vmin=0, vmax=255)
    plt.title(sel)
    plt.show()
    plt.close()

入力＝０

入力＝１

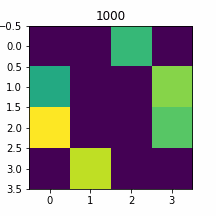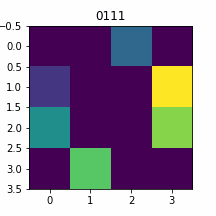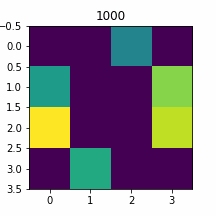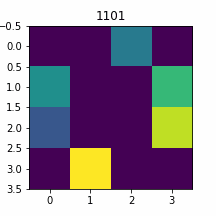
びゃあ゛ぁぁうまひぃいぃぃ゛ぃぃぃい！！！やっぱり量子コンピュータで（以下略

おわりに

今回使った量子ビットは28個。もう少し節約できます。オーバーヘッドで16マスよりも多く使っていますが、スケールアップしたときにきっとお得になると信じています (・ε・｀)ﾎﾝﾏｶｲﾅ

次回、お待ちを