量子ゲートでピクセルアートを作る（③8✕8サイズ準備編）

AI要約
はじめに
８×８サイズはどえらい
ブロック１
ブロック２
ブロック３
ブロック４
ブロック５
ブロック６
合体
おわりに

AI要約

量子ゲートのサンプリングで8×8サイズのネコを描くための準備編です。元画像と6ビット値の対応を確認し、このサイズ特有の難しさや設計上の課題を整理しながら、次の実装段階への道筋を示しました。

はじめに

前回は量子ゲートのサンプリングで「ヒキガエル」を描画しました。

今回からいよいよ８✕８サイズのネコを作っていきます。

８×８サイズはどえらい

まずはネコの画像とその元になる６ビットの値を眺めてみましょう。

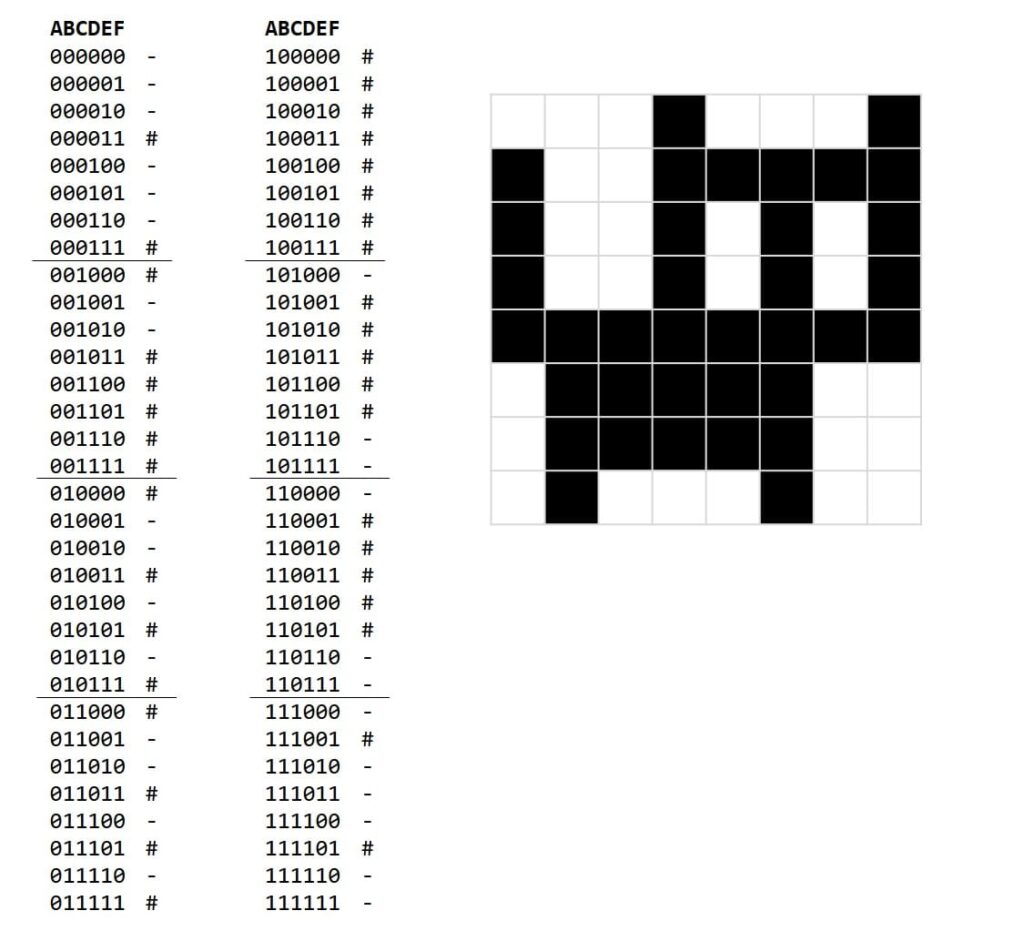
うーん、これは ╮(︶﹏︶”)╭

前回までの方法で黒マスの６ビットだけを生成する論理式を作るのは無理です。

そこで考え方を変えて、ある６ビット乱数が与えられたときに、そのマスを塗るか塗らないか判定する論理式を作ってみます。ABCDEFから論理式を作ってネコを塗りつぶすってことですね。

ブロック１

いきなりブロック１と言われても。

これからネコをいくつかのブロックで塗っていきます。最後にORで合成すればネコになるというわけです。

それにしても６ビットの論理合成っつったってしんどい。６ビットのカルノー図は習ってないですよ。なんとかいい感じの塊を見つけて効率的に塗っていきます。

まずはこの部分に着目します。

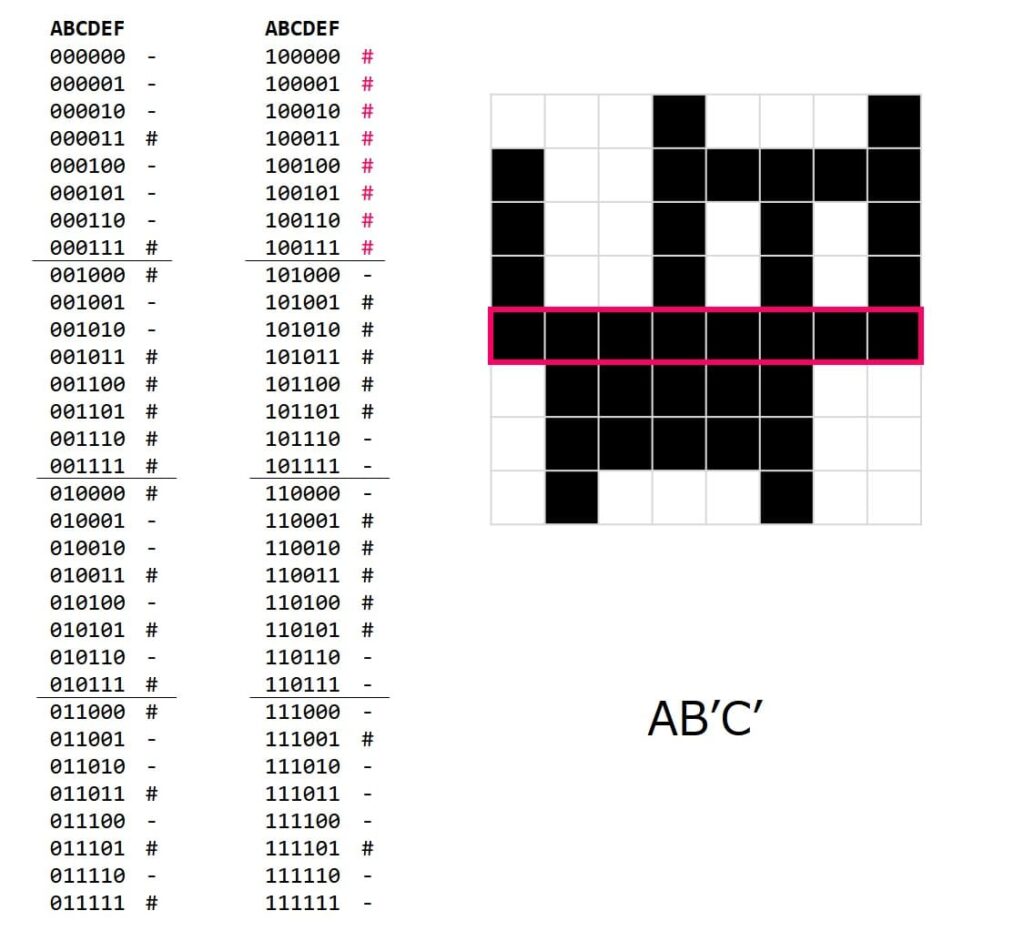
ここは簡単ですね。上位ビット＝１００でキレイに絞れるので、論理式は「AB’C’」です。

ではこれで本当に塗れるのか確認します。観測するのは６ビットの乱数とこのブロックの論理合成結果であることに注意してください。

import numpy as np
import matplotlib.pyplot as plt
from qiskit import QuantumCircuit
from qiskit_aer import AerSimulator


def NOT(i, j):
    global qc
    """
    (NOT i) -> j
    """
    qc.cx(i, j)
    qc.x(j)

def AND(i, j, k):
    global qc
    """
    (i AND j) -> k
    """
    qc.ccx(i, j, k)

def XOR(i, j, k):
    global qc
    """
    (i XOR j) -> k
    """
    qc.cx(i, k)
    qc.cx(j, k)

def OR(i, j, k):
    global qc
    """
    (i OR j) -> k
    """
    qc.x(i)
    qc.x(j)
    qc.ccx(i, j, k)
    qc.x(i)
    qc.x(j)
    qc.x(k)


#初期化
qc = QuantumCircuit(37)

#6ビット（64通り）の乱数を作る
qc.h(0) # A
qc.h(1) # B
qc.h(2) # C
qc.h(3) # D
qc.h(4) # E
qc.h(5) # F

#便利のため、各NOTを用意
NOT(0, 6) # A'
NOT(1, 7) # B'
NOT(2, 8) # C'
NOT(3, 9) # D'
NOT(4, 10) # E'
NOT(5, 11) # F'

#ブロック1
AND(0, 7, 12) # AB'
AND(12, 8, 13) # AB'C'


#サンプリング
qc.measure_all()
backend = AerSimulator(method='matrix_product_state')
result = backend.run(qc, shots=500).result().get_counts()

#確認
pos = (0, 1, 2, 3, 4, 5, 13)
box = np.zeros(64, 'uint8')
base = np.array([2**5, 2**4, 2**3, 2**2, 2**1, 2**0], int)

for r in result:
    sel = ''.join(r[::-1][p] for p in pos)
    #乱数ビット
    bit = np.array(list(sel[:6]), int)
    #ブロック判定ビット
    judge = bool(int(sel[-1]))
    if judge:
        #10進数ワンホットに戻す
        idx = np.sum(base * bit)
        box[idx] = 255

img = box.reshape(8, 8)
plt.imshow(img, vmin=0, vmax=255)
plt.show()
plt.close()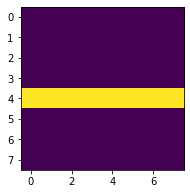

500回サンプリングして、論理合成結果が１の結果に限って６ビット乱数を64マスにデコードして塗っています。論理合成結果が０の解はスルーしています。

結果、きちんと目的のマスだけが塗れることが確認できました。

ブロック２

どんどんいきましょう。今度はここを塗ります。

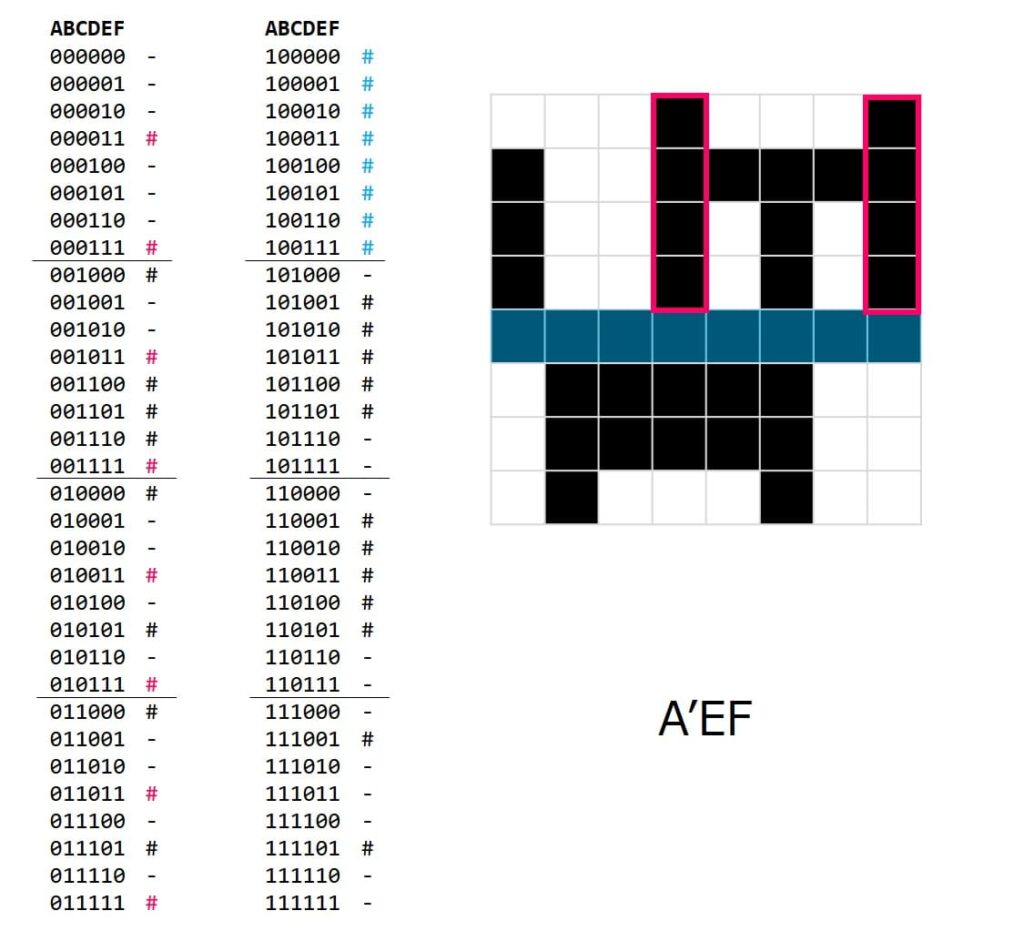
ここも比較的簡単です。画像の上半分なので最上位ビット＝０、かつ、下位ビット＝１１で絞ることができます。

コードを延長して確認。

#ブロック2
AND(6, 4, 14) # A'E
AND(14, 5, 15) # A'EF

pos = (0, 1, 2, 3, 4, 5, 15)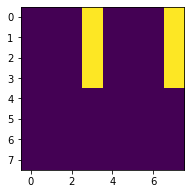

できていますね。

ブロック３

次は少しトリッキーな塗り方をします。

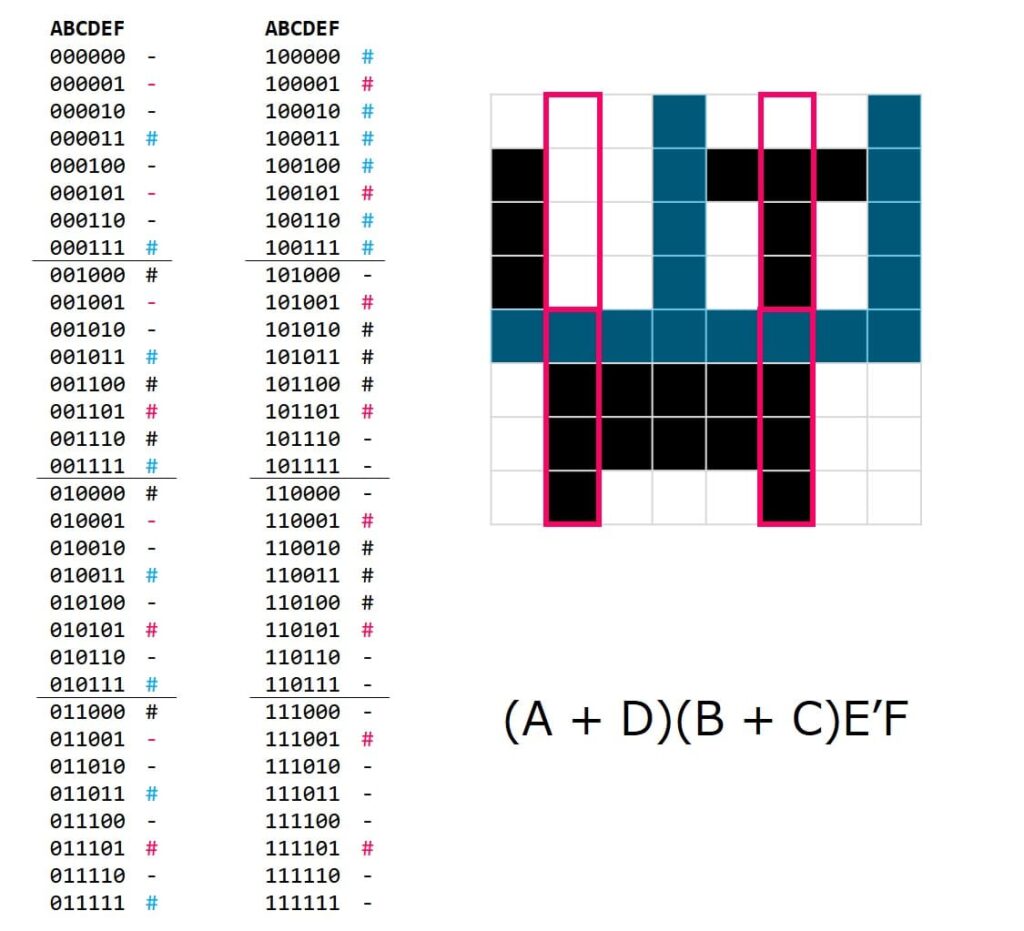
これわかりますかね？縦の４連をORで塗る、かつ、大きな４象限で見たときにもORで絞る。ORが２重になってるんですね。

まるでORのロマネスコやぁ（数学科大爆笑）

確認します。

#ブロック3
OR(0, 3, 16) # (A + D)
OR(1, 2, 17) # (B + C)
AND(16, 17, 18) # (A + D)(B + C)
AND(18, 10, 19) # (A + D)(B + C)E'
AND(19, 5, 20) # (A + D)(B + C)E'F

pos = (0, 1, 2, 3, 4, 5, 20)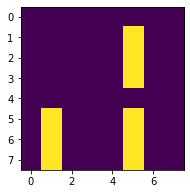

OK牧場。

ブロック４

尻尾を塗ります。

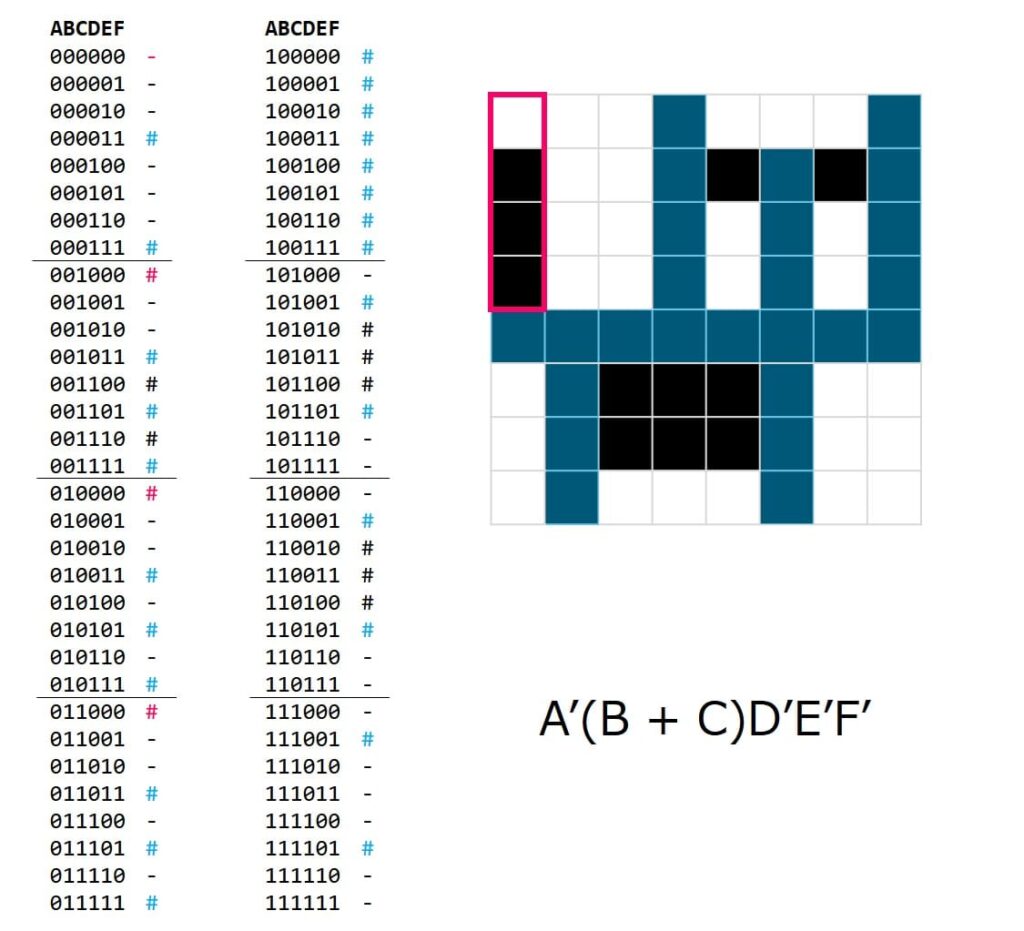
こんなのでも５次式になるんかい。って思いました。（６次式は絶対に使いたくない）

#ブロック4
AND(6, 17, 21) # A'(B + C)
AND(21, 9, 22) # A'(B + C)D'
AND(22, 10, 23) # A'(B + C)D'E'
AND(23, 11, 24) # A'(B + C)D'E'F'

pos = (0, 1, 2, 3, 4, 5, 2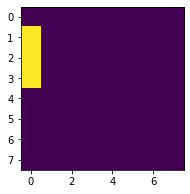4)

順調なり。

ブロック５

ボディを埋めます。

過去に塗った場所を２度塗りしても大丈夫です。XORを使った式をひねり出して３次式に収めてみました。

#ブロック5
XOR(1, 2, 25) # (B ⊕ C)
XOR(3, 4, 26) # (D ⊕ E)
AND(0, 25, 27) # A(B ⊕ C)
AND(27, 26, 28) # A(B ⊕ C)(D ⊕ E)

pos = (0, 1, 2, 3, 4, 5, 2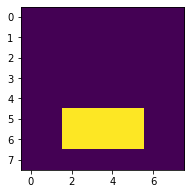8)

いいですね。

ブロック６

ラストです。

#ブロック6
AND(6, 7, 29) # A'B'
AND(29, 2, 30) # A'B'C
AND(30, 3, 31) # A'B'CD

pos = (0, 1, 2, 3, 4, 5, 3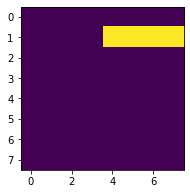1)

ここは簡単でしたね。

合体

ブロック１～６をORしたつもりで塗ってみましょう。量子回路上で統合はしていません。ブロック判定ビット列に１が一つでもあれば、そのときの乱数ビット→10進数→対応マスを塗る、としています。

#確認
pos = (0, 1, 2, 3, 4, 5, 13, 15 ,20, 24, 28, 31)
box = np.zeros(64, 'uint8')
base = np.array([2**5, 2**4, 2**3, 2**2, 2**1, 2**0], int)

for r in result:
    sel = ''.join(r[::-1][p] for p in pos)
    #乱数ビット
    bit = np.array(list(sel[:6]), int)
    #ブロック判定ビット列
    judge = list(sel[-6:])
    if '1' in judge:
        #10進数ワンホットに戻す
        idx = np.sum(base * bit)
        box[idx] = 255

img = box.reshape(8, 8)
plt.imshow(img, vmin=0, vmax=255)
plt.show()
plt.close()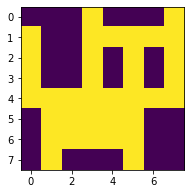

ネコ～ ฅ^•ω•^ฅ

おわりに

さあ、ここからどうやってサンプリングで画像生成まで持っていくのか。次回をお楽しみに。