蓮コラ画像が含まれます。集合体恐怖症の方はご注意ください。
問題
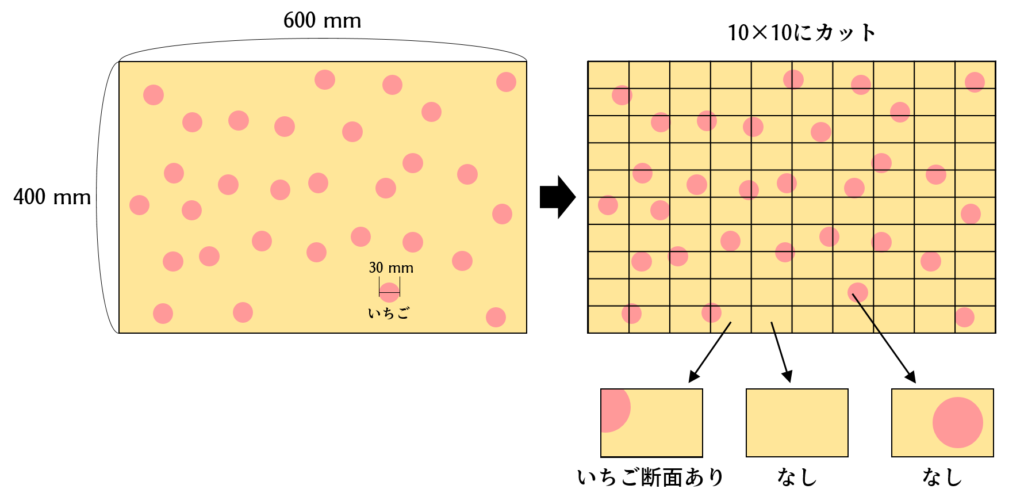
次のような、断面にいちごが見える四角いケーキを作りたい。しかし、いちごのコストは削減したい。
よこ60cm、たて40cmのスポンジ生地に、直径3cmのいちごを散りばめる。生地を10×10個にカットしたとき、少なくとも1つのいちご断面を有するピースが90%以上となるいちごの最小個数を求めよ。
今回は数学をまったく使わずに、モンテカルロ法で答えを求めてみます。
数学ができない
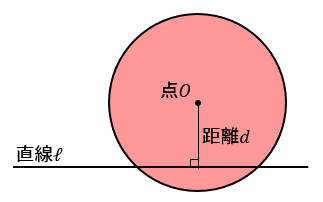
大の大人が3人集まって理論で解こうとあれこれ考えてみましたが、「点と直線の距離」の公式が思い出せず断念しました。
通りかかった数学科出身の人に聞いてみたところ、
あーめんどくさい。(主に境界条件が)
と言われました。
参考文献
モンテカルロ法とは、ある値や確率が知りたいときに、コンピュータ内でサイコロを振りまくって実験的に求める方法です。
実行環境
WinPython3.6をおすすめしています。
Google Colaboratoryが利用可能です。

import
必要なパッケージをインポートします。
import numpy as np
import numpy.random as nr
from copy import deepcopy
import matplotlib.pyplot as plt
from PIL import Image, ImageDrawいちごの用意
いちごの画像を作ります。透明な四角の上に半透明な赤い円を置きます。R値は255、αチャンネルは100としました。
#いちご(透明な四角の上に半透明な赤い円を置いたもの)
ichigo = Image.new('RGBA', (31, 31), (0, 0, 0, 0))
draw_ichigo = ImageDraw.Draw(ichigo)
draw_ichigo.ellipse((0, 0, 30, 30), fill=(255, 0, 0, 100))
#表示
plt.imshow(ichigo)
plt.show()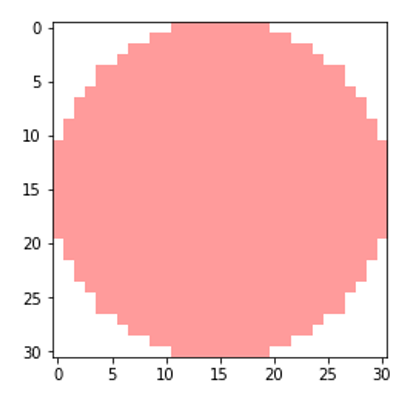
ケーキの用意
ケーキの画像を作ります。ただの透明な四角です。
#ケーキ(透明な四角)
cake = Image.new('RGBA', (600, 400), (0, 0, 0, 0))
#表示
plt.imshow(cake)
plt.show()
ケーキにいちごを100個置いてみる
「ケーキにいちごを置く」関数を作って、100回実行してみます。
#受け取ったケーキのランダムな位置にいちごを置いて返す関数
def put_ichigo(cake_tmp):
x, y = nr.randint(0, 600-30), nr.randint(0, 400-30)
cake_tmp.paste(ichigo, (x, y), ichigo) #透過画像として貼り付け
return cake_tmp
#ケーキにいちごを100個置く
for i in range(100):
cake = put_ichigo(cake)
#表示
plt.imshow(cake)
plt.show()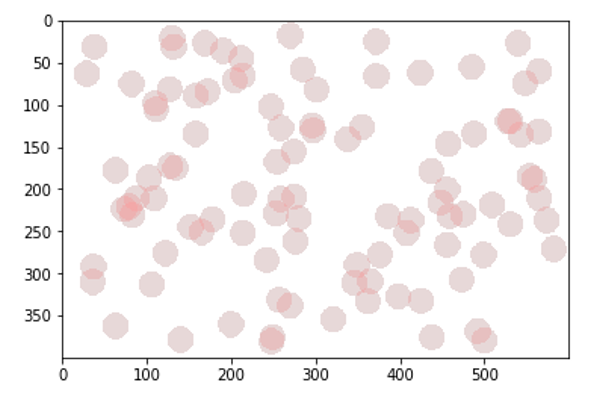
いちごが重ならないように置くには?
いちごをわざわざ透過画像にしたのには理由があります。いちご1個の部分はRGBのR成分が100ですが、いちごが2つ以上重なった部分はRが100より大きくなります。したがって、ケーキのR成分の最大値を調べることでいちごが重なっているかどうかを判断できます。
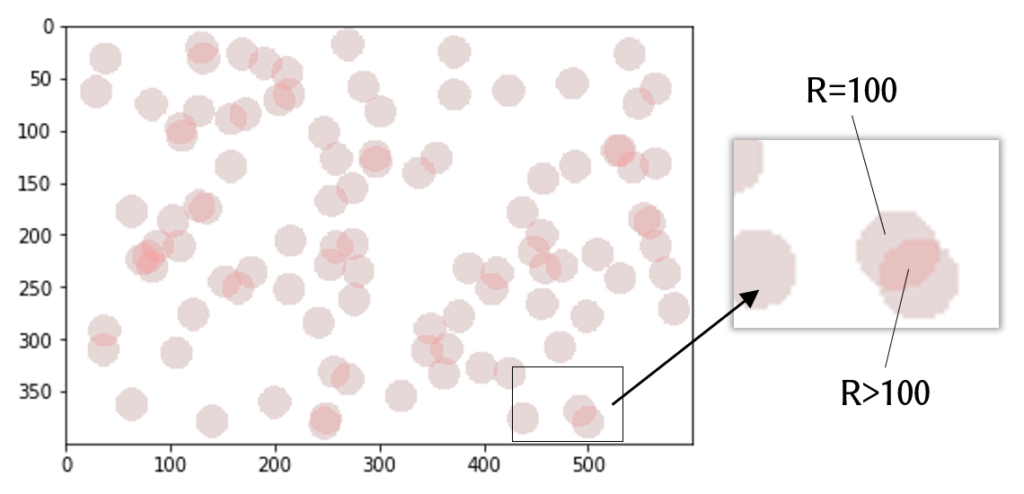
これを利用して、いちごが重ならないように100個置いてみます。
#受け取ったケーキの赤成分の最大値を返す関数
def get_redmax(cake_tmp):
cake_np = np.array(cake_tmp)
return np.max(cake_np[:,:,0])
#ケーキにいちごを100個置く。ただしイチゴが重なった場合は置き直す
ichigo_count = 0
while 1:
#ケーキをコピーしていちごを置いてみる
cake_copy = deepcopy(cake)
cake_copy = put_ichigo(cake_copy)
#いちごが重なっていなければ採用する
if get_redmax(cake_copy) <= 100:
cake = deepcopy(cake_copy)
ichigo_count += 1
#いちごが100個乗ったら終わり
if ichigo_count == 100:
break
#表示
plt.imshow(cake)
plt.show()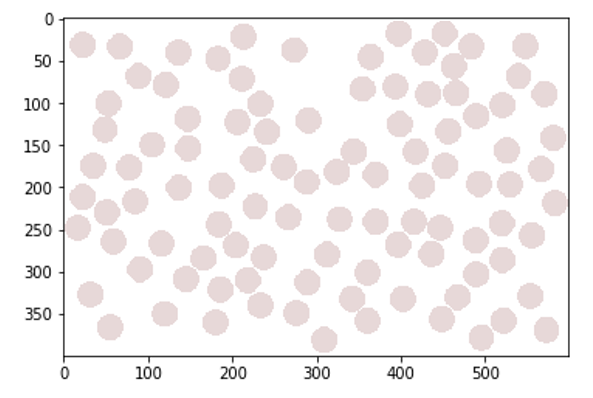
いちご断面があるかどうかの判断は?
ケーキを1ピースにカットしたとき、ピースの外周にR成分=100の部分があれば、そのピースにはいちご断面があるといえます。そこで、「ケーキをカットして1ピースを返す関数」「ピースの外周の赤成分の最大値を返す関数」を作ります。このケーキの全ピースを調べて、「いちご断面があるピース数」「全ピース数」を数えます。
#受け取ったケーキをカットして1ピースを返す関数
def cut_cake(cake_tmp, x, y):
piece = cake_tmp.crop((x, y, x+60, y+40))
return piece
#受け取ったピースの外周の赤成分の最大値を返す関数
def get_redmax_edge(cake_tmp):
cake_np = np.array(cake_tmp)
edge = np.concatenate([cake_np[0,:,0], cake_np[-1,:,0], cake_np[:,0,0], cake_np[:,-1,0]])
return np.max(edge)
#ケーキを10×10にカットして「断面にいちごがあるピース数」と「全ピース数」を数える
ok_count = 0
all_count = 0
for x in range(0, 600, 60):
for y in range(0, 400, 40):
#カット
piece = cut_cake(cake, x, y)
#いちご断面があればOKカウントする
if get_redmax_edge(piece) == 100:
ok_count += 1
#すべてのピースをカウントする
all_count += 1
print('ok_count:{}'.format(ok_count))
print('all_count:{}'.format(all_count))ok_count:98
all_count:100100ピース中98ピースにいちご断面がありました。90%のピース(=90個)にいちご断面があればよいので、いちごを100個散りばめるのはちょっと無駄があるといえます。
サイコロを振りまくる
ここまでのコードを少し改造して(コードは省略)、いちごの数を0~100個、各1000回試行して平均値と標準偏差をプロットすると次のようになりました。
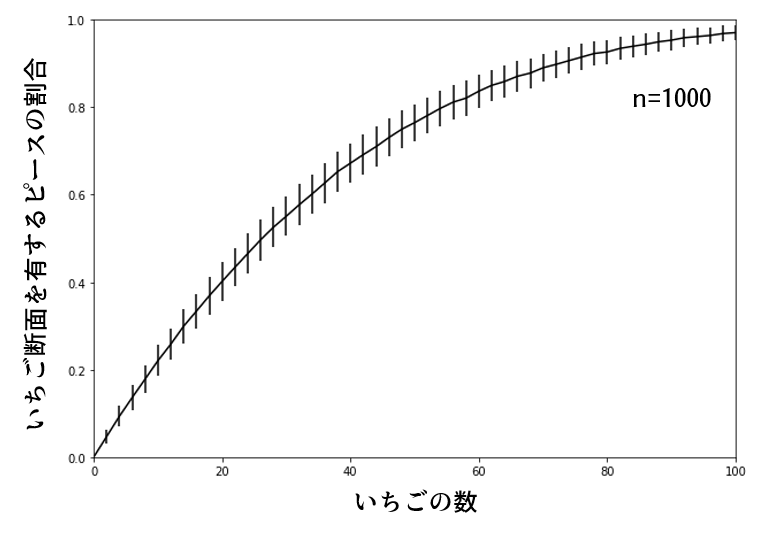
(略)
ichigo_num:72 mean:0.89919
ichigo_num:73 mean:0.90160
ichigo_num:74 mean:0.90704
ichigo_num:75 mean:0.91067
(略)結論、いちごを73個散りばめれば90%以上のピースにいちご断面があらわれることが期待される。


