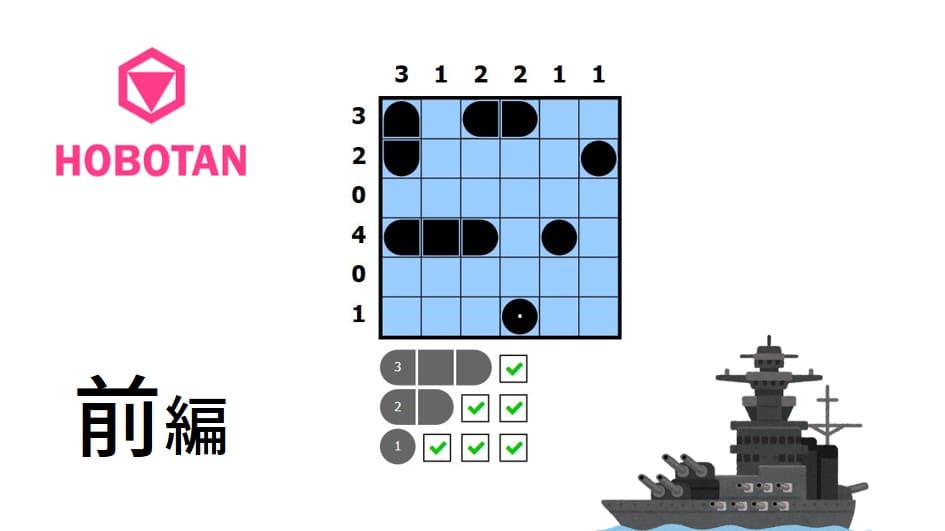
やること
これまでQUBOアニーリングの教材を作ってきましたが、昨年、HOBO対応の疑似アニーリングパッケージ「HOBOTAN」が登場しました。
QUBO(2つの量子ビットの相互作用)では解けなかった問題がHOBO(3個以上の量子ビットの相互作用)で解けるようになります。ここではペンシルパズルの一つ、「海戦パズル(バトルシップ)」(英名:Battleships)を定式化して解いてみましょう。
※この記事はQUBOアニーリングの基礎講座を履修済みであることを前提としています。
TYTANについて
前身となる「TYTAN」はOSSの疑似量子アニーリングパッケージです。
日本量子コンピューティング協会が運営しているチュートリアル教材はこちら。
私のオンライン講義でよければこちらから見れます。
discordコミュニティもあるので気軽に質問できます。
HOBOTANについて
それを元にしてできたのが「HOBOTAN」。使い方はTYTANとほとんど同じです。分からないことがあれば何でも聞いてください。
海戦パズルとは
コンセプティスパズル さんから問題をお借りします。感謝いたします。
ルールは、お絵かきロジックのように各行、各列とも指定した数のマスを黒く塗ります(=船)。最終的に1×1サイズの船を3個、2×1サイズの船を2個、3×1サイズの船を1個配置します。各船の8近傍に他の船があってはいけません。
答えはこちらです。
いつもお世話になっているPuzzle Team さんでも無限に遊べます。
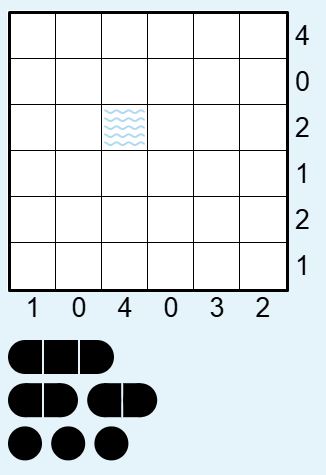
予備実験(1×1の船)
まずは6×6フィールドに1×1サイズの船を3個置くというのをQUBO(またはHOBO)で実装してみます。HOBOTANはQUBOも内包しているので、パッケージとしてはHOBOTANだけで大丈夫です。
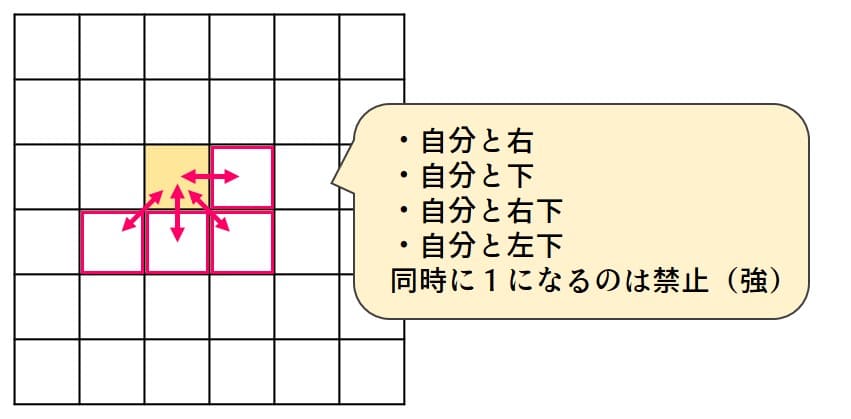
2次元配列状に量子ビットを用意し、全体で3個だけ1にします(強い条件)。このままだと8近傍に他の船が入ってしまうので、それを禁止するために「自分と右、自分と下、自分と右下、自分と左下は同時に塗られない」という条件を追加します(これも強い条件)。
from hobotan import *
import numpy as np
import matplotlib.pyplot as plt
#量子ビットの用意
q = symbols_list([6, 6], 'q{}_{}')
#全体で3マス塗る
Hconst = (np.sum(q) - 3)**2
#自分と右、自分と下、自分と右下、自分と左下は同時に塗られない
for i in range(6):
for j in range(5):
Hconst += q[i, j]*q[i, j+1]
for i in range(5):
for j in range(6):
Hconst += q[i, j]*q[i+1, j]
for i in range(5):
for j in range(5):
Hconst += q[i, j]*q[i+1, j+1]
for i in range(5):
for j in range(1, 6):
Hconst += q[i, j]*q[i+1, j-1]
#式の合体
H = Hconst
#HOBOテンソルにコンパイル
hobo, offset = Compile(H).get_hobo()
print(f'offset\n{offset}')
#サンプラー選択
solver = sampler.MIKASAmpler()
#サンプリング
result = solver.run(hobo, shots=100)
#上位4件
for r in result[:4]:
print(f'Energy {r[1]}, Occurrence {r[2]}')
#さくっと配列に
arr, subs = Auto_array(r[0]).get_ndarray('q{}_{}')
#さくっと画像に
img, subs = Auto_array(r[0]).get_image('q{}_{}')
plt.figure(figsize=(3, 3))
plt.imshow(img)
plt.show()tensor order = 2
----- compile -----
MODE: GPU
DEVICE: cuda:0
-------------------
offset
9.0
===== sampler =====
MODE: GPU
DEVICE: cuda:0
===================
.......... 100/2000 min=9.0 mean=63.48999786376953
.......... 200/2000 min=3.0 mean=51.86000061035156
.......... 300/2000 min=3.0 mean=44.37999725341797
(中略)
.......... 1800/2000 min=-9.0 mean=9.829999923706055
.......... 1900/2000 min=-9.0 mean=7.62999963760376
.......... 2000/2000 min=-9.0 mean=3.4099998474121094
Energy -9.0, Occurrence 1
(画像)
Energy -9.0, Occurrence 1
(画像)
Energy -9.0, Occurrence 1
(画像)
Energy -9.0, Occurrence 1
(画像)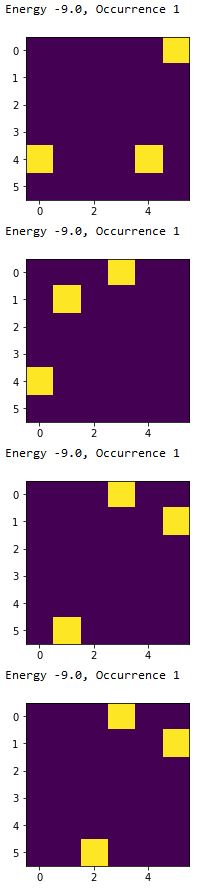
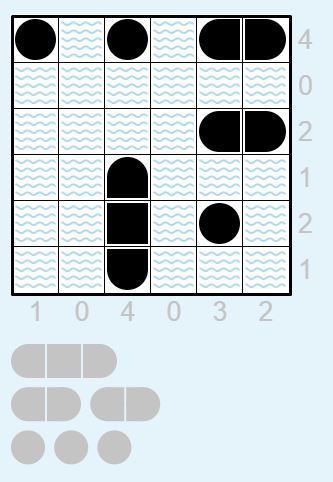
オフセットが9.0、解のエネルギーが-9.0ということで理想的な解が無数に得られました。成功です。
予備実験(3×1の船)
次に、3×1の船をやります。
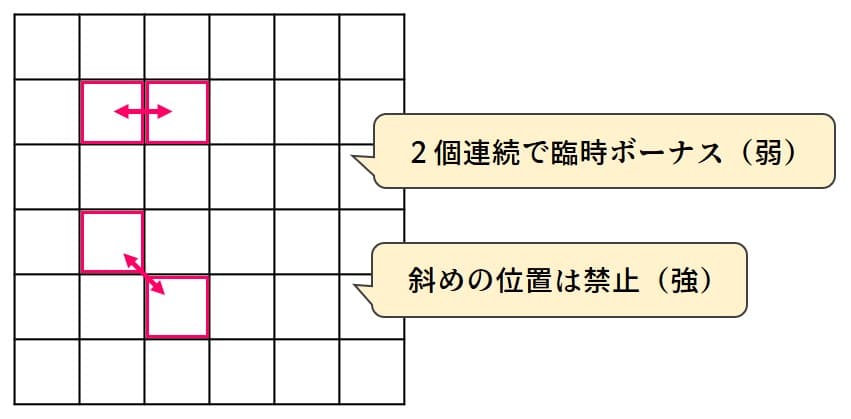
全体で3個だけ1にします(強い条件)。このままだとバラバラになるので、隣り合うマスが連続で塗られたら臨時ボーナスを与えます(弱い条件、この理由が分からない方はTYTAN講座「No.5 お席へどうぞ」「No.6 お絵かきロジック」を再履修、もしくは「量子アニーリング(QUBO)でお絵かきロジック(ロジックアート、ピクロス)を解く」)。
この臨時ボーナスは最大で2個GETできますが、L字になってしまう可能性があります。これを排除するために「斜めのマスが同時に塗られたら臨時ペナルティ」を追加します(強い条件)。
from hobotan import *
import numpy as np
import matplotlib.pyplot as plt
#量子ビットの用意
q = symbols_list([6, 6], 'q{}_{}')
#全体で3マス塗る
Hconst = (np.sum(q) - 3)**2
#隣り合うマスが連続で塗られたら臨時ボーナス
Hcost = 0
for i in range(6):
for j in range(5):
Hcost += -q[i, j]*q[i, j+1]
for j in range(6):
for i in range(5):
Hcost += -q[i, j]*q[i+1, j]
#斜めのマスが同時に塗られたら臨時ペナルティ
for i in range(5):
for j in range(5):
Hconst += q[i, j]*q[i+1, j+1]
for i in range(5):
for j in range(1, 6):
Hconst += q[i, j]*q[i+1, j-1]
#式の合体
H = Hconst + 0.1*Hcost
#HOBOテンソルにコンパイル
hobo, offset = Compile(H).get_hobo()
print(f'offset\n{offset}')
#サンプラー選択
solver = sampler.MIKASAmpler()
#サンプリング
result = solver.run(hobo, shots=100)
#上位4件
for r in result[:4]:
print(f'Energy {r[1]}, Occurrence {r[2]}')
#さくっと配列に
arr, subs = Auto_array(r[0]).get_ndarray('q{}_{}')
#さくっと画像に
img, subs = Auto_array(r[0]).get_image('q{}_{}')
plt.figure(figsize=(3, 3))
plt.imshow(img)
plt.show()tensor order = 2
----- compile -----
MODE: GPU
DEVICE: cuda:0
-------------------
offset
9.0
===== sampler =====
MODE: GPU
DEVICE: cuda:0
===================
.......... 100/2000 min=17.899999618530273 mean=63.460994720458984
.......... 200/2000 min=1.8999996185302734 mean=47.21400451660156
.......... 300/2000 min=-0.10000038146972656 mean=38.15999984741211
(中略)
.......... 1800/2000 min=-9.200000762939453 mean=7.403998851776123
.......... 1900/2000 min=-9.200000762939453 mean=4.676999568939209
.......... 2000/2000 min=-9.200000762939453 mean=1.7129992246627808
Energy -9.200000762939453, Occurrence 1
(画像)
Energy -9.200000762939453, Occurrence 5
(画像)
Energy -9.200000762939453, Occurrence 3
(画像)
Energy -9.200000762939453, Occurrence 2
(画像)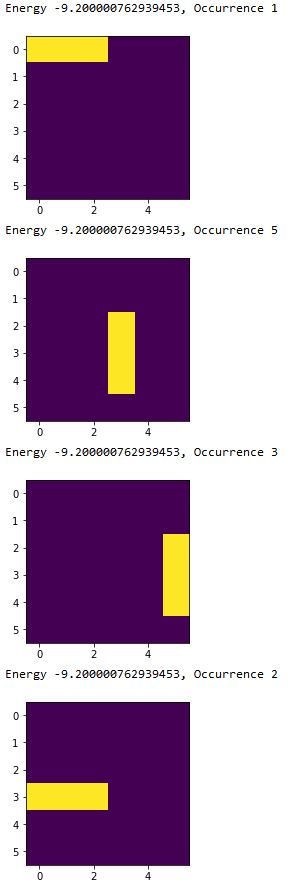
オフセットが9.0、解のエネルギーが-9.20です。臨時ボーナスを0.1倍にしてあるので、それが2個で-0.2です。こちらもうまくいきました。
予備実験(2×1の船)
さて、2×1が少し大変です。
2×1の船は2個あるので全体で4個だけ1にします(強い条件)。こちらもバラバラにならないように、隣り合うマスが連続で塗られたら臨時ボーナスを与えます(弱い条件)。そしてやはりL字や「田の字」になることを防ぐために「斜めのマスが同時に塗られたら臨時ペナルティ」を追加します(強い条件)。
ここまでは3×1の設定と同じですので、結果として4×1が塗られます。
2個の2×1に分けるためには、「直線の3マスが連続で塗られたら臨時ペナルティ」を与えます(強い条件)。これはHOBOTANのチュートリアルにある「教室の席にできるだけ多くの生徒を座らせる(ただし縦・横に3席連続で座ってはいけない)」と同じ設定です(誰も見てねぇよそんなページ)。この条件に3次の項が登場するため、QUBOではなくHOBOである必要があるのです。
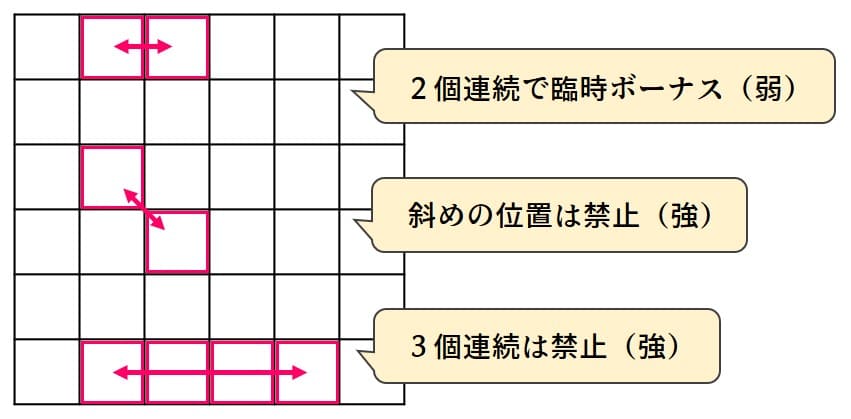
※補足:「斜めマスのペナルティ」によって他の船が8近傍に入ることも防げています。
from hobotan import *
import numpy as np
import matplotlib.pyplot as plt
#量子ビットの用意
q = symbols_list([6, 6], 'q{}_{}')
#全体で4マス塗る
Hconst = (np.sum(q) - 4)**2
#隣り合うマスが連続で塗られたら臨時ボーナス
Hcost = 0
for i in range(6):
for j in range(5):
Hcost += -q[i, j]*q[i, j+1]
for j in range(6):
for i in range(5):
Hcost += -q[i, j]*q[i+1, j]
#斜めのマスが同時に塗られたら臨時ペナルティ
for i in range(5):
for j in range(5):
Hconst += q[i, j]*q[i+1, j+1]
for i in range(5):
for j in range(1, 6):
Hconst += q[i, j]*q[i+1, j-1]
#直線の3マスが連続で塗ったら臨時ペナルティ
for i in range(6):
for j in range(6 - 3 + 1):
Hconst += np.prod(q[i, j:j+3])
for j in range(6):
for i in range(6 - 3 + 1):
Hconst += np.prod(q[i:i+3, j])
#式の合体
H = Hconst + 0.1*Hcost
#HOBOテンソルにコンパイル
hobo, offset = Compile(H).get_hobo()
print(f'offset\n{offset}')
#サンプラー選択
solver = sampler.MIKASAmpler()
#サンプリング
result = solver.run(hobo, shots=100)
#上位4件
for r in result[:4]:
print(f'Energy {r[1]}, Occurrence {r[2]}')
#さくっと配列に
arr, subs = Auto_array(r[0]).get_ndarray('q{}_{}')
#さくっと画像に
img, subs = Auto_array(r[0]).get_image('q{}_{}')
plt.figure(figsize=(3, 3))
plt.imshow(img)
plt.show()tensor order = 3
----- compile -----
MODE: GPU
DEVICE: cuda:0
-------------------
offset
16.0
===== sampler =====
MODE: GPU
DEVICE: cuda:0
===================
.......... 100/2000 min=0.6999998092651367 mean=39.58599853515625
.......... 200/2000 min=-11.100000381469727 mean=28.54399871826172
.......... 300/2000 min=-11.100000381469727 mean=22.060998916625977
(中略)
.......... 1800/2000 min=-16.200000762939453 mean=1.6459972858428955
.......... 1900/2000 min=-16.200000762939453 mean=-0.42400145530700684
.......... 2000/2000 min=-16.200000762939453 mean=-4.641001224517822
Energy -16.200000762939453, Occurrence 1
(画像)
Energy -16.200000762939453, Occurrence 1
(画像)
Energy -16.200000762939453, Occurrence 1
(画像)
Energy -16.200000762939453, Occurrence 1
(画像)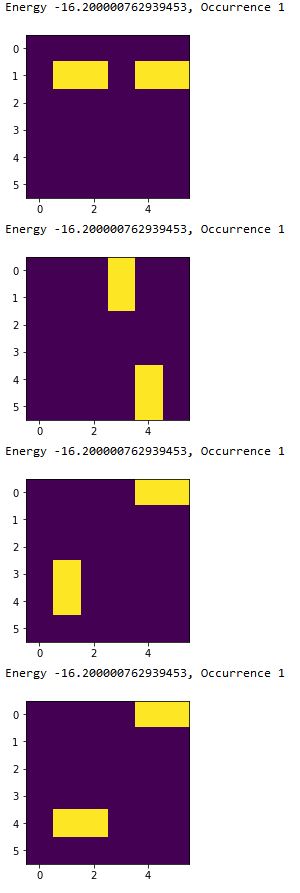
最新バージョンではコンパイル時に「tensor order = 3」のようにテンソルの次元が表示されます。3以上がHOBOです。
オフセットが16.0、解のエネルギーが-16.20ということで、こちらも臨時ボーナス-0.2を獲得しています。
やはりHOBO・・・!! HOBOは全てを解決する・・・!!
おわりに
準備は整いました。後編に続きます。