やること
HOBOで「海戦パズル（バトルシップ）」（英名：Battleships）を解くシリーズの後編です。
いよいよパズルを解きますが、コード量が多いのでしっかりコーヒーをキメて挑んでください。
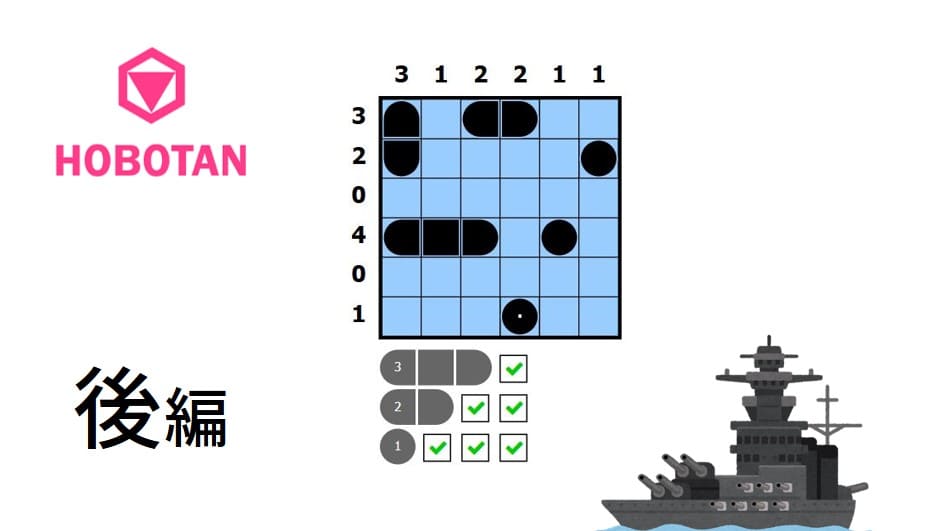
海戦パズル（再掲）
コンセプティスパズル さんから拝借した問題です。
Puzzle Team さんでも無限に遊べます。
予備実験したものを合体
前回作った要素を合体します。量子ビットは6x6x3で定義して、各レイヤーに1×1、2×1、3×1の船を割り当てます。
ここで、レーヤ―間に新しい制約が必要になります。今のままではいけないと思います。だからこそ、制約は今のままではいけないと思っています。 今のままだと、異なるレーヤ―の船が重なってしまったり、互いに８近傍に侵入してしまう可能性があります。レーヤ―をまたいで近傍への侵入を禁止するために、次の図のように「自分と他レイヤーの18各マスは同時に１にならない」という条件を追加します（強い条件）。(๑•́ ₃ •̀๑) ﾂﾀﾜﾚ
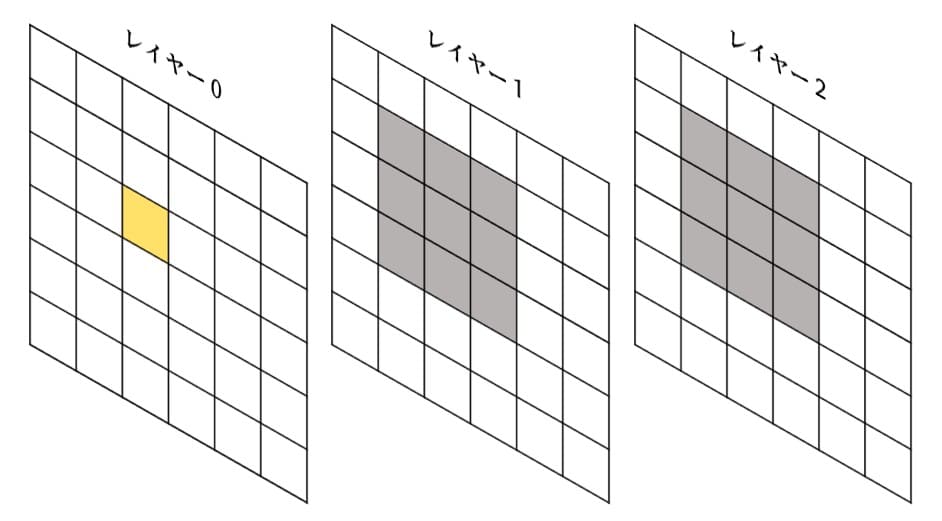
また、すっかり忘れ気味でしたが行と列の数字制約もあります。これは お絵かきロジック や 温度計パズル でやったのと同じです。あと、初期で水マス（＝０）が確定しているマスもあるので設定してください。
最終的なコードです。
from hobotan import *
import numpy as np
import matplotlib.pyplot as plt
#量子ビットを用意
q = symbols_list([6, 6, 3], 'q{}_{}_{}')
#式を用意
Hconst = 0
Hcost = 0
'''
1x1の船
'''
#レイヤー全体で3マス塗る
Hconst += (np.sum(q[:, :, 0]) - 3)**2
#自分と右、自分と下、自分と右下、自分と左下は同時に塗られない
for i in range(6):
for j in range(5):
Hconst += q[i, j, 0]*q[i, j+1, 0]
for i in range(5):
for j in range(6):
Hconst += q[i, j, 0]*q[i+1, j, 0]
for i in range(5):
for j in range(5):
Hconst += q[i, j, 0]*q[i+1, j+1, 0]
for i in range(5):
for j in range(1, 6):
Hconst += q[i, j, 0]*q[i+1, j-1, 0]
'''
2x1の船
'''
#レイヤー全体で4マス塗る
Hconst += (np.sum(q[:, :, 1]) - 4)**2
#隣り合うマスが連続で塗られたら臨時ボーナス
for i in range(6):
for j in range(5):
Hcost += -q[i, j, 1]*q[i, j+1, 1]
for j in range(6):
for i in range(5):
Hcost += -q[i, j, 1]*q[i+1, j, 1]
#斜めのマスが同時に塗られたら臨時ペナルティ
for i in range(5):
for j in range(5):
Hconst += q[i, j, 1]*q[i+1, j+1, 1]
for i in range(5):
for j in range(1, 6):
Hconst += q[i, j, 1]*q[i+1, j-1, 1]
#直線の3マスが連続で塗ったら臨時ペナルティ
for i in range(6):
for j in range(6 - 3 + 1):
Hconst += np.prod(q[i, j:j+3, 1])
for j in range(6):
for i in range(6 - 3 + 1):
Hconst += np.prod(q[i:i+3, j, 1])
'''
3x1の船
'''
#レイヤー全体で3マス塗る
Hconst += (np.sum(q[:, :, 2]) - 3)**2
#隣り合うマスが連続で塗られたら臨時ボーナス
for i in range(6):
for j in range(5):
Hcost += -q[i, j, 2]*q[i, j+1, 2]
for j in range(6):
for i in range(5):
Hcost += -q[i, j, 2]*q[i+1, j, 2]
#斜めのマスが同時に塗られたら臨時ペナルティ
for i in range(5):
for j in range(5):
Hconst += q[i, j, 2]*q[i+1, j+1, 2]
for i in range(5):
for j in range(1, 6):
Hconst += q[i, j, 2]*q[i+1, j-1, 2]
'''
レーヤ―間の追加設定
'''
#あるマスと他のレイヤーの3x3領域は同時に塗られない
for i in range(6):
for j in range(6):
#相手のあぶり出し
tmp0 = []
tmp1 = []
tmp2 = []
if i-1 >= 0 and j-1 >= 0:
tmp0.append(q[i-1, j-1, 0])
tmp1.append(q[i-1, j-1, 1])
tmp2.append(q[i-1, j-1, 2])
if i-1 >= 0:
tmp0.append(q[i-1, j, 0])
tmp1.append(q[i-1, j, 1])
tmp2.append(q[i-1, j, 2])
if i-1 >= 0 and j+1 < 6:
tmp0.append(q[i-1, j+1, 0])
tmp1.append(q[i-1, j+1, 1])
tmp2.append(q[i-1, j+1, 2])
if j-1 >= 0:
tmp0.append(q[i, j-1, 0])
tmp1.append(q[i, j-1, 1])
tmp2.append(q[i, j-1, 2])
tmp0.append(q[i, j, 0])
tmp1.append(q[i, j, 1])
tmp2.append(q[i, j, 2])
if j+1 < 6:
tmp0.append(q[i, j+1, 0])
tmp1.append(q[i, j+1, 1])
tmp2.append(q[i, j+1, 2])
if i+1 < 6 and j-1 >= 0:
tmp0.append(q[i+1, j-1, 0])
tmp1.append(q[i+1, j-1, 1])
tmp2.append(q[i+1, j-1, 2])
if i+1 < 6:
tmp0.append(q[i+1, j, 0])
tmp1.append(q[i+1, j, 1])
tmp2.append(q[i+1, j, 2])
if i+1 < 6 and j+1 < 6:
tmp0.append(q[i+1, j+1, 0])
tmp1.append(q[i+1, j+1, 1])
tmp2.append(q[i+1, j+1, 2])
#レーヤ―0視点、それらと同時に塗れない
for s in tmp1 + tmp2:
Hconst += q[i, j, 0] * s
#レーヤ―1視点、それらと同時に塗れない
for s in tmp0 + tmp2:
Hconst += q[i, j, 1] * s
#レーヤ―2視点、それらと同時に塗れない
for s in tmp0 + tmp1:
Hconst += q[i, j, 2] * s
'''
問題の反映
'''
#横方向の合計
h = [4, 0, 2, 1, 2, 1]
for i in range(6):
Hconst += (np.sum(q[i, :, :]) - h[i])**2
#縦方向の合計
v = [1, 0, 4, 0, 3, 2]
for j in range(6):
Hconst += (np.sum(q[:, j, :]) - v[j])**2
#初期で決まっているマス
Hconst += (np.sum(q[2, 2, :]) - 0)**2
#式の合体
H = Hconst + 0.1*Hcost
#HOBOテンソルにコンパイル
hobo, offset = Compile(H).get_hobo()
print(f'offset\n{offset}')
#サンプラー選択
solver = sampler.MIKASAmpler()
#サンプリング
result = solver.run(hobo, shots=1000, T_num=50000)
#上位1件
for r in result[:1]:
print(f'Energy {r[1]}, Occurrence {r[2]}')
#さくっと配列に
arr, subs = Auto_array(r[0]).get_ndarray('q{}_{}_{}')
#レイヤー確認
plt.figure(figsize=(3, 3))
plt.imshow((arr[:, :, 0]*255).astype('uint8'))
plt.show()
plt.figure(figsize=(3, 3))
plt.imshow((arr[:, :, 1]*255).astype('uint8'))
plt.show()
plt.figure(figsize=(3, 3))
plt.imshow((arr[:, :, 2]*255).astype('uint8'))
plt.show()tensor order = 3
----- compile -----
MODE: GPU
DEVICE: cuda:0
-------------------
offset
90.0
===== sampler =====
MODE: GPU
DEVICE: cuda:0
===================
.......... 1000/50000 min=308.1000061035156 mean=697.7960205078125
.......... 2000/50000 min=308.1000061035156 mean=640.9459228515625
.......... 3000/50000 min=246.59999084472656 mean=601.093505859375
（中略）
.......... 48000/50000 min=-90.4000015258789 mean=-69.29000091552734
.......... 49000/50000 min=-90.4000015258789 mean=-70.6550064086914
.......... 50000/50000 min=-90.4000015258789 mean=-77.21591186523438
Energy -90.4000015258789, Occurrence 2
（画像）
（画像）
（画像）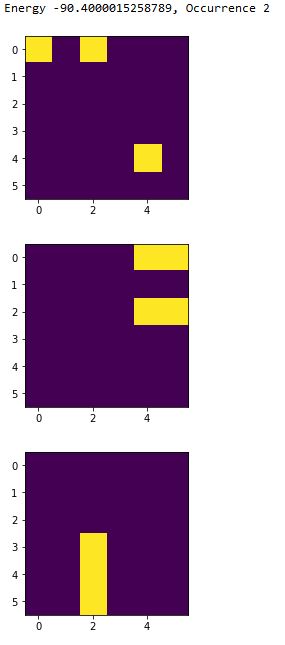
一致してますね？オフセットが90.0、解のエネルギーが-90.40です。前回確認したように臨時ボーナスが-0.4あるはずなので理論通りです。
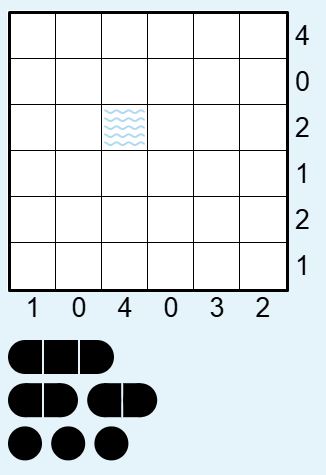
別の問題でも確認
Puzzle Team さんからも１問拝借しました。
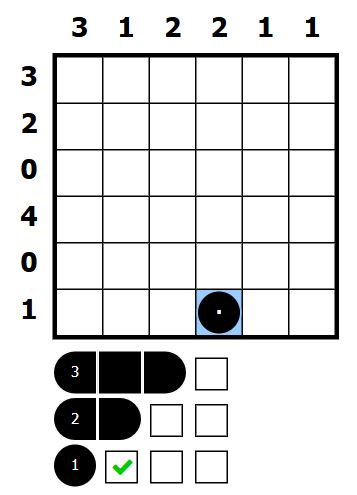
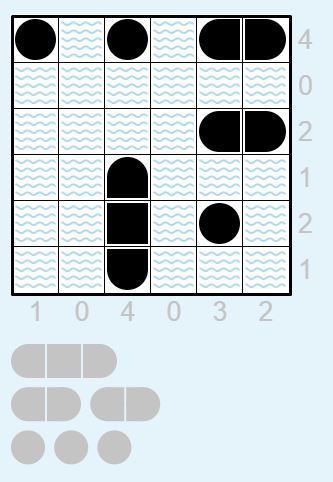
答えはこちら
'''
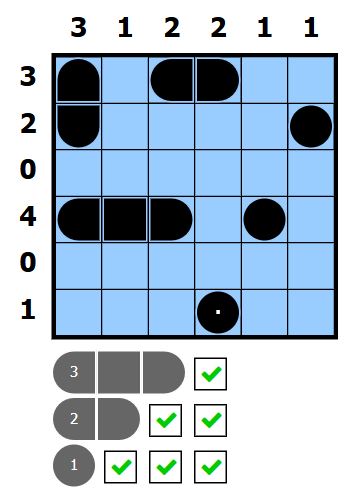
問題の反映
'''
#横方向の合計
h = [3, 2, 0, 4, 0, 1]
for i in range(6):
Hconst += (np.sum(q[i, :, :]) - h[i])**2
#縦方向の合計
v = [3, 1, 2, 2, 1, 1]
for j in range(6):
Hconst += (np.sum(q[:, j, :]) - v[j])**2
#初期で決まっているマス
Hconst += (q[5, 3, 0] - 1)**2tensor order = 3
----- compile -----
MODE: GPU
DEVICE: cuda:0
-------------------
offset
85.0
===== sampler =====
MODE: GPU
DEVICE: cuda:0
===================
.......... 1000/50000 min=363.5 mean=693.305419921875
.......... 2000/50000 min=245.8000030517578 mean=638.341796875
.......... 3000/50000 min=245.8000030517578 mean=597.1168823242188
（中略）
.......... 48000/50000 min=-85.39999389648438 mean=-64.34429931640625
.......... 49000/50000 min=-85.39999389648438 mean=-65.36650085449219
.......... 50000/50000 min=-85.39999389648438 mean=-71.82839965820312
Energy -85.39999389648438, Occurrence 2
（画像）
（画像）
（画像）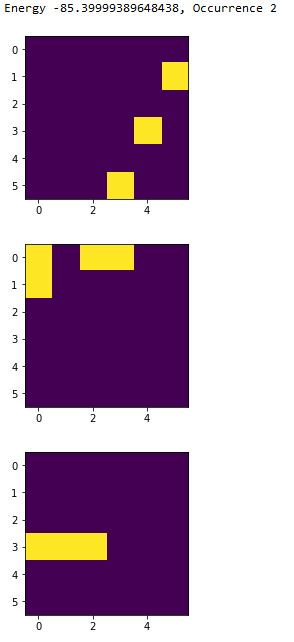
こちらも無事に解けました！
おわりに
HOBOが使えるようになったことで解けるパズルが大幅に増えました（全然解けそうにないやつらもいるんですけどねぇ）。皆さんの参考になるような例を公開していきたいと思います。
普段あまりお願いすることはないのですが、参考になったと思ったら是非リアクションをお願いします。ページ下部に「この記事をシェアする」欄があるのでそこからTwitterでツイートするなど目に見えるアクションを歓迎しています。また、ブログで使用する場合は必ず引用を忘れずに！エンジニア同士のマナーを大切にネ！
