AI要約
遺伝的アルゴリズム「vcopt」を用いて、掘削ルートの最適化に挑戦しました。マリオパーティのミニゲーム「はっくつ!ハッスル!!」を例に、遺伝的アルゴリズムがどのようにルート選定を効率化できるのかを解説。最適解を導き出すプロセスやアルゴリズムを紹介します。
やること
ルート最適化の依頼がありましたので、今回はお仕事紹介です。
マリオパーティに「はっくつ!ハッスル!!」というミニゲームがあります。30秒以内に決められたライン上をドリルで掘って、その正確性を競います。お題がテレサであればこのように外周をなぞります。

採点アルゴリズムは謎です。(有志による解析では再現率(Recall)であることが示唆されており、太線でグリグリ塗ることで100点が取れるとか?)

さて、今回の依頼は「決められたラインをすべて掘削する最短ルート」を計算するシステムの開発です。さっそくアルゴリズムを見ていきましょう。
事前知識
この記事ではお手軽最適化パッケージ「vcopt」を使用します。詳細はチュートリアルをご参照ください。
vcopt関連の記事はこちらです。

問題
問題となるノードとエッジを定義しました。※「はっくつ!ハッスル!!」とはルールが違うのであちらは一旦忘れてください!
こちらがノード番号です。
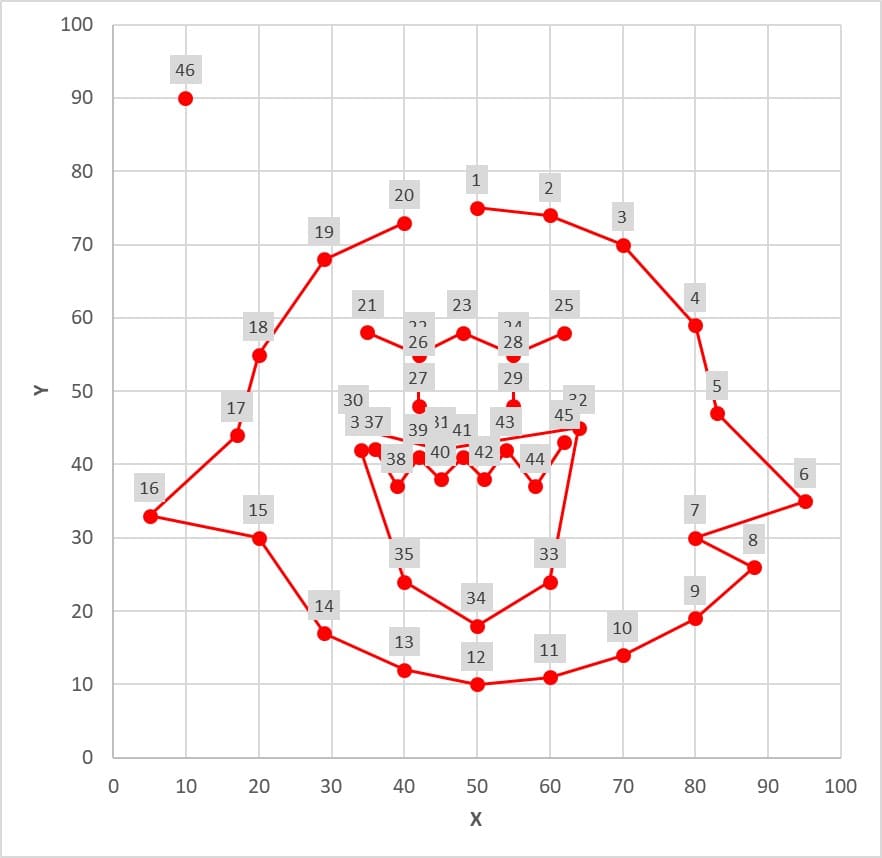
こちらが掘削が必要なエッジです。エッジはどちら側から掘ってもOKです。
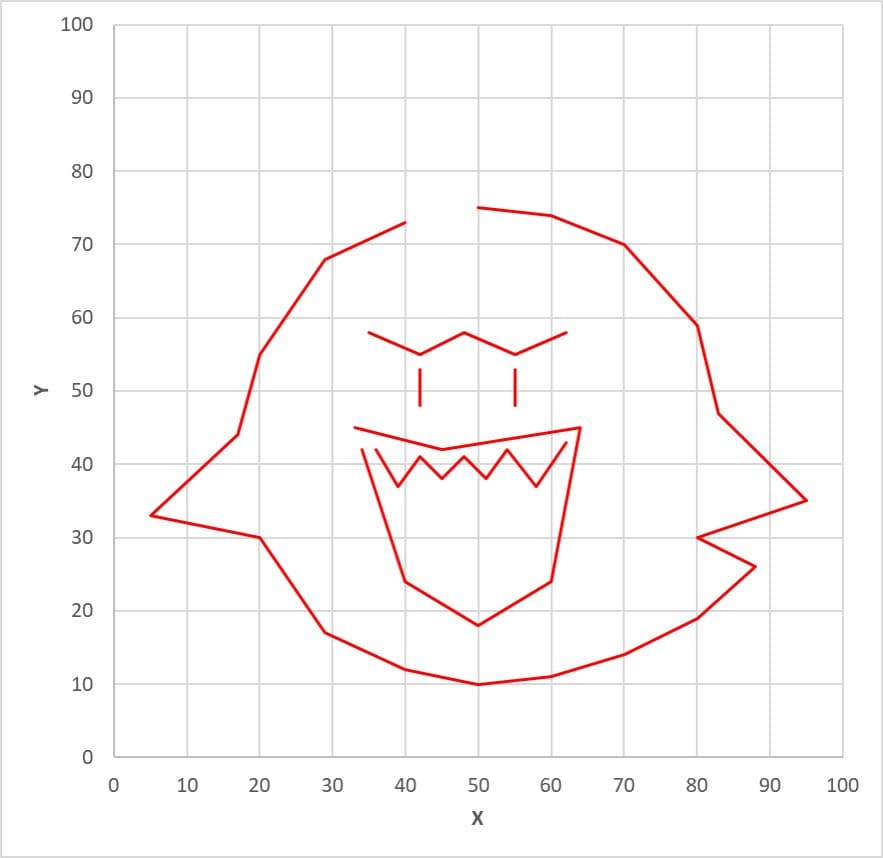
離れた場所にノード46を置いていて、これは掘削と無関係ですが、ここをスタート地点・ゴール地点に設定したいと思います。また、移動スピード:掘るスピード=10:1とします。
入力情報はこのような3つのcsvファイルです(クリックで拡大)。
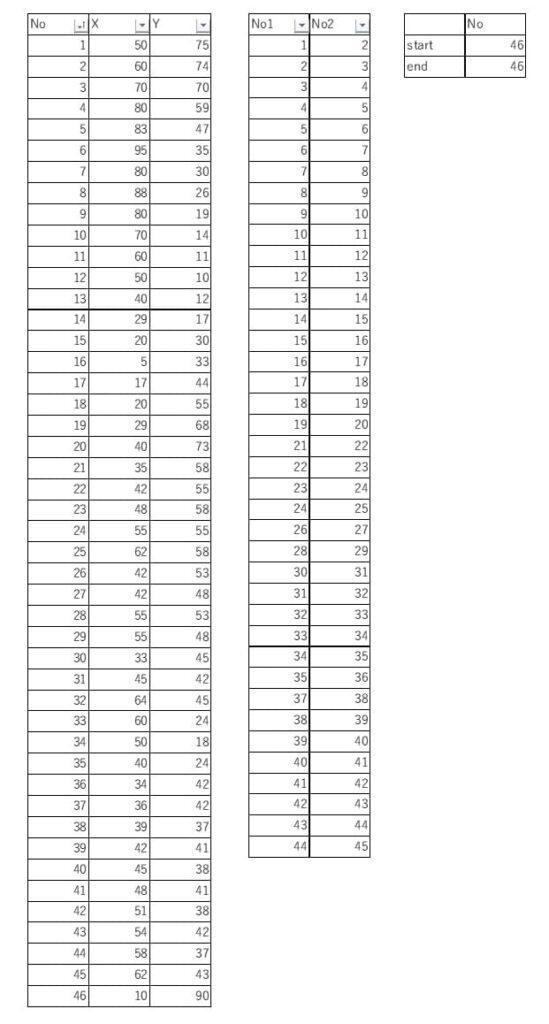
前処理
入力情報をすべて読み込み、一筆書きで繋がるノードたちをグループ化します。次のような6グループにまとまりました。
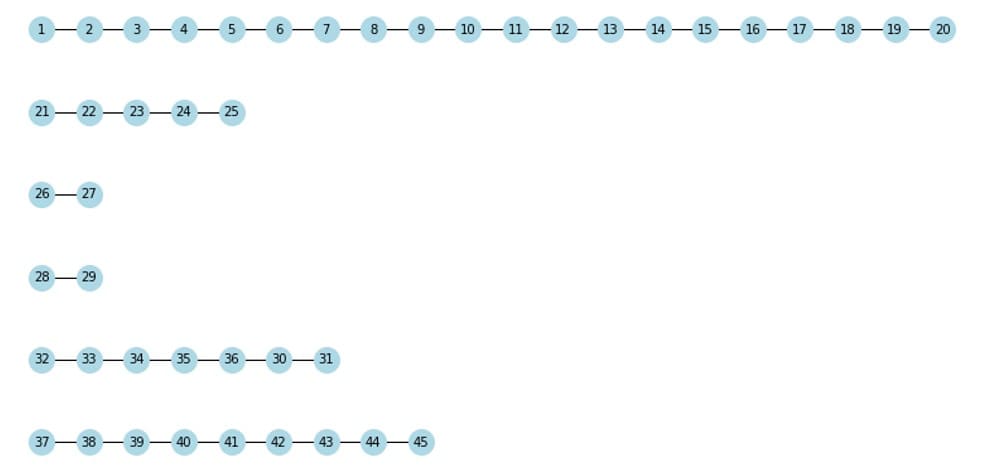
これを上から順にG1, G2, …, G6と呼ぶことにします。G5の表示がちょっとバグっていますが内部的には正しく認識されているのでご心配なく。
遺伝子の設計
いよいよ遺伝的アルゴリズム(GA)でルート最適化します。今回は専用のGAを書くのではなく、vcoptで用意されている順序最適化の関数を使うことにします。
vcopt().tspGA() は、遺伝子配列 [0, 1, 2, a, b, c] と評価関数を与えると、最適化して [1, c, b, 0, a, 2] のように順序を並び替えた解を返してくれます。このように6地点を最短で回るルートを求めるならそのまま適用できますね。
しかし、今回は点ではなく線(ノードではなくエッジ)を回るルートの最適化です。そしてエッジの通り方には正方向と逆方向の2パターンあります。これをどのように遺伝子に落とし込むのでしょうか?
こういう方法があります。
[G1, G2, G3, G4, G5, G6, -G1, -G2, -G3, -G4, -G5, -G6] という遺伝子を用意します。「G1」はグループ1を正方向に掘ること、「-G1」は逆方向に掘ることを意味します。
これを並び替えると、例えば [G1, -G5, -G2, G5, G4, -G1, G6, -G6, -G3, G2, G3, -G4] という遺伝子になります。評価関数では、左から順に見てプラスとマイナスのうち最初に登場したものを拾います。つまり、 [G1, -G5, -G2, G5, G4, -G1, G6, -G6, -G3, G2, G3, -G4] の赤字の部分を抽出して [G1, -G5, -G2, G4, G6, -G3] という遺伝子を得ます。あとはこのルートの距離を計算して評価値を返します。
このようにすると汎用の vcopt().tspGA() で対応できるようになるんですね。もちろんこの方法はベストではないので、本気を出すなら専用のGAを書いたほうがいいです。
最適化
最適化は次のように実行します。
#GAで最適化
model = vcopt()
para, score = model.tspGA(para_range, #並び替えたい遺伝子
tsp_score, #評価関数
0.0) #目標値「para」と「score」には第1位の解が返ってきます。paraからノード番号を復元したものがシステムの出力となります(クリックで拡大)。

以下のようにすると進化が終わった集団全体を取得・集計することができます。ベスト6まで図示してみます。
#解集団の取得
pool = model.pool
pool_score = model.pool_scoreこちらが第1位(と第2位)です。同一スコア(2.186点)で逆方向の関係です。
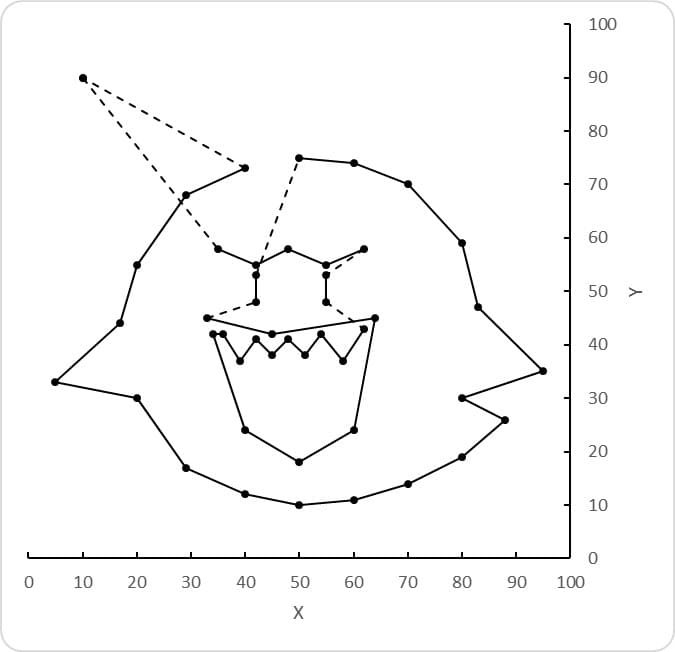
第3位(と第4位)です。スコアは2.191。
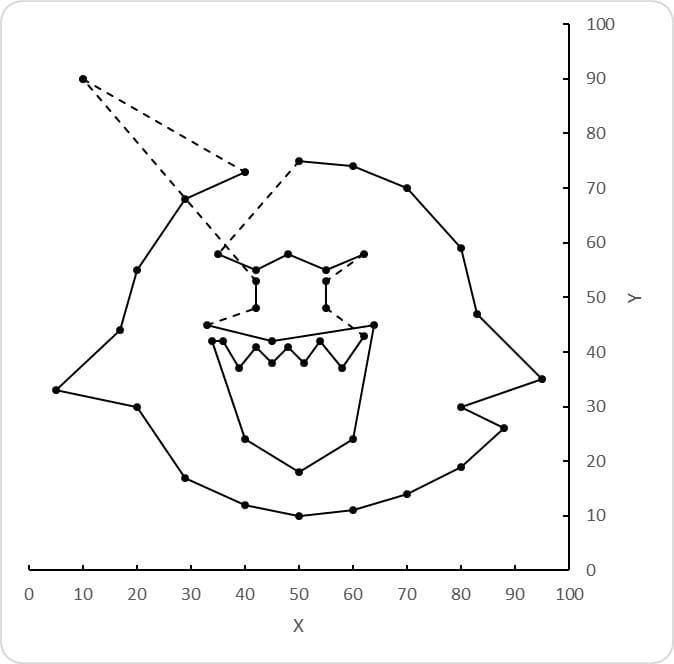
第5位(と第6位)です。スコアは2.194。
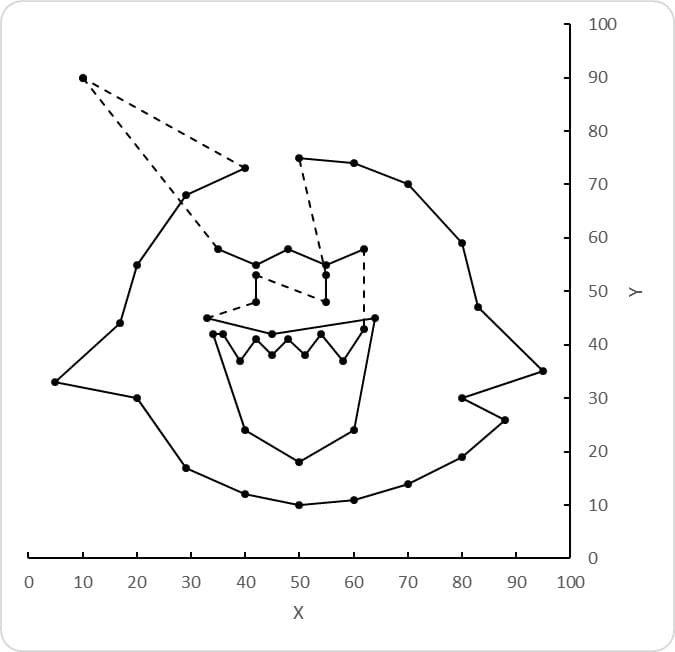
良さそうですね!
おわりに
納品前にいくつかのテストケースで良い解が出るようにパラメータを調整します。例えば、エッジが超細切れのケースでは、グループ化がほとんど行われないため最適化のステップが非常に重たくなります。現実的な時間に収めようとすると解の品質が悪いまま終了してしまいます。このように課題をあぶり出して解決しておくことで、納品後のトラブルが減って使い勝手がぐっと上がります。テストケースの設計は非常に大切と言えます。
また、今回は一筆書きでエッジをグループ化しましたが、そうしないほうが早くなるケースも考えられます。これは次のフェーズで対応することにしましょう。
よい最適化ライフを(*゚▽゚)ノ


