AI要約
量子ゲートで7セグメントLEDを作るシリーズの第2弾。単一セグメントの点灯制御に焦点を当て、各ビットの状態によって適切にON/OFFを切り替える量子回路を設計しました。
やること
前回はQiskitでNOT, AND, XOR, ORゲートを扱うことができました。
今回はいよいよ7セグメントLEDの各バーを光らせる計算を考えます。何が入力で何が出力なのかを意識して読んでみてください。

やりたいこと
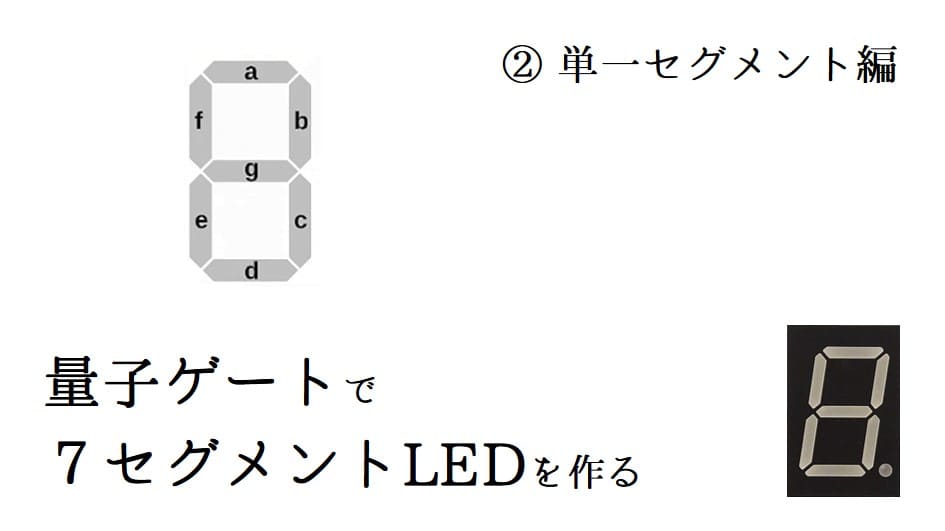
7セグメントLEDは7本のバーの点灯・消灯を制御することで0~9の数字を表示するものです。見たことありますよね。各バーにはa~gまで名前がついています。

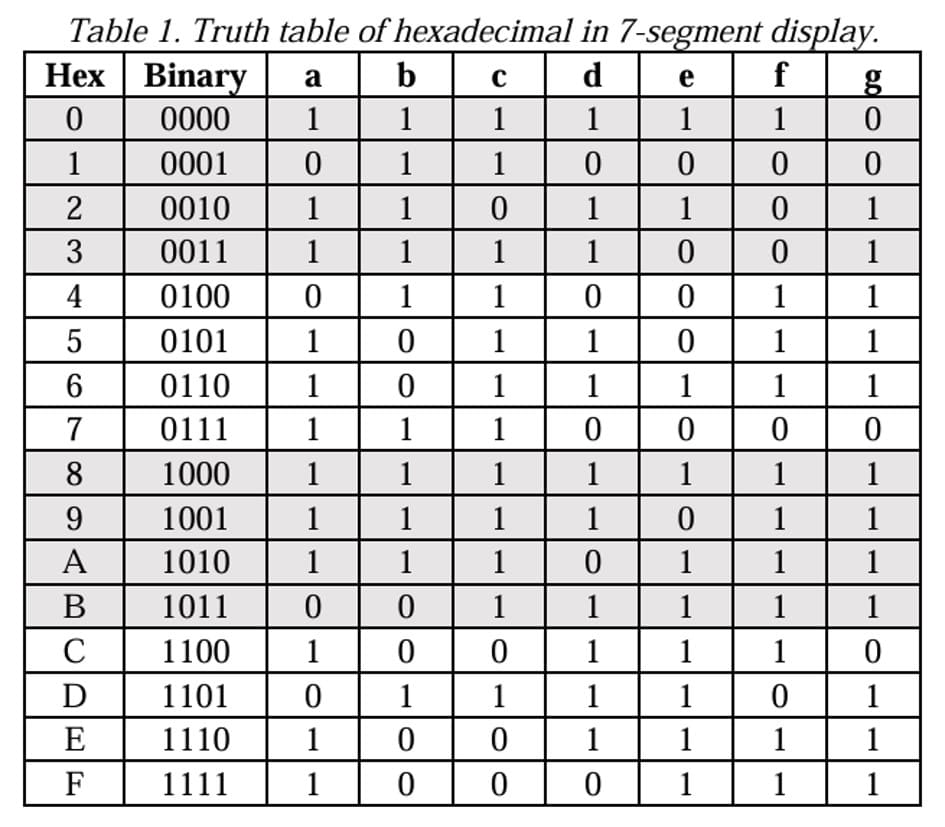
今回は4量子ビットを入力として、0~Fの16通りの出力を計算することを考えます。すなわち、[0000] →「0の表示」、[1111] →「Fの表示」といった対応です。この対応一覧が次のとおりです。
で、結局、何がしたいのかというと以下の通り。ここが一番大事!
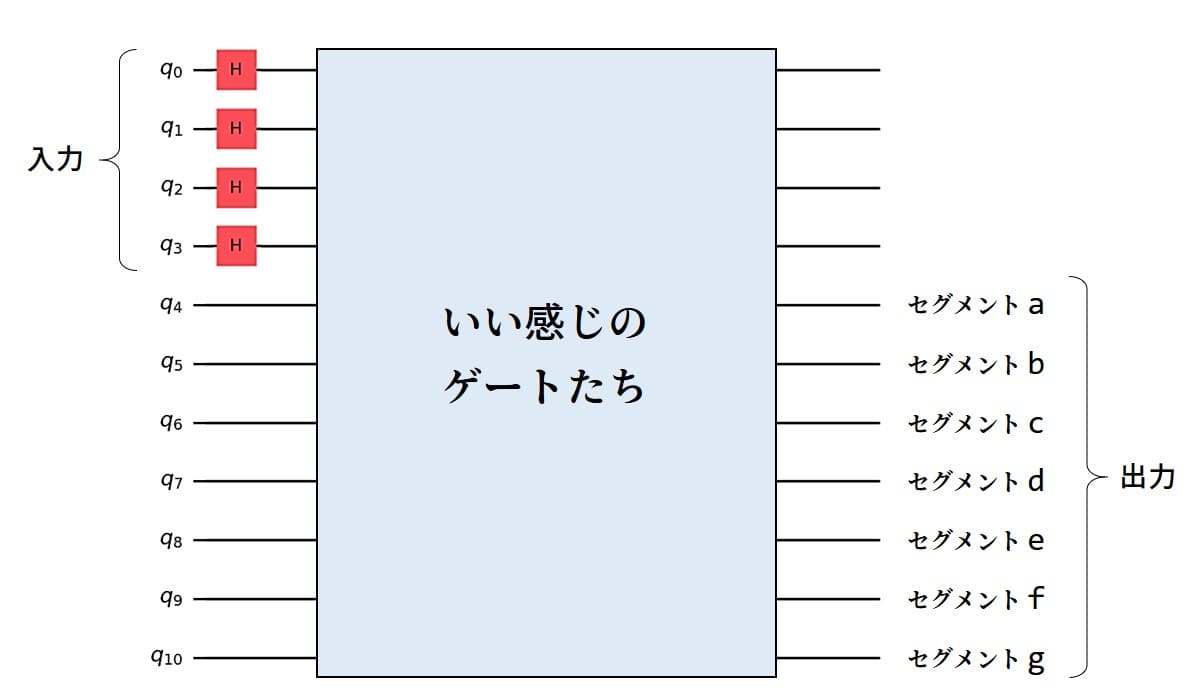
4量子ビットの入力が与えたれたとき、その数字を表示するための各バーの状態を計算したいのです。しかも、入力は [0000] ~ [1111] までの16通りが同時に与えられ、すべてのパターンで正しくLEDが点灯するような共通の「いい感じのゲートたち」を配置するというゲームです。
うん、これはやばそうだ。
例えば入力が [0000] だけであれば簡単ですね。[0000] → [1, 1, 1, 1, 1, 1, 0] を作ればいいのですから、雑に6個をXゲートで反転してやれば完成です。入力情報を使わなくても済みます。しかし、[0000] → [1, 1, 1, 1, 1, 1, 0] と [0001] → [0, 1, 1, 0, 0, 0, 0] を同時に満たすことを考えるともう降参です。16通りすべてで正しい出力になるゲートを置かなければならないのです。
理論
で、まあこういう理論は工学部の基礎でやられていて、例えばこちらの海外の授業テキスト(?)に答えが書かれています。(0~9だけの7セグメントデコーダの文献は多いですが、0~Fまでカバーしている文献は非常に少ないようです)
Buege Mahara Putra, Designing a 7-Segment Display Circuit for Hexadecimal Numbers Using Karnaugh Maps
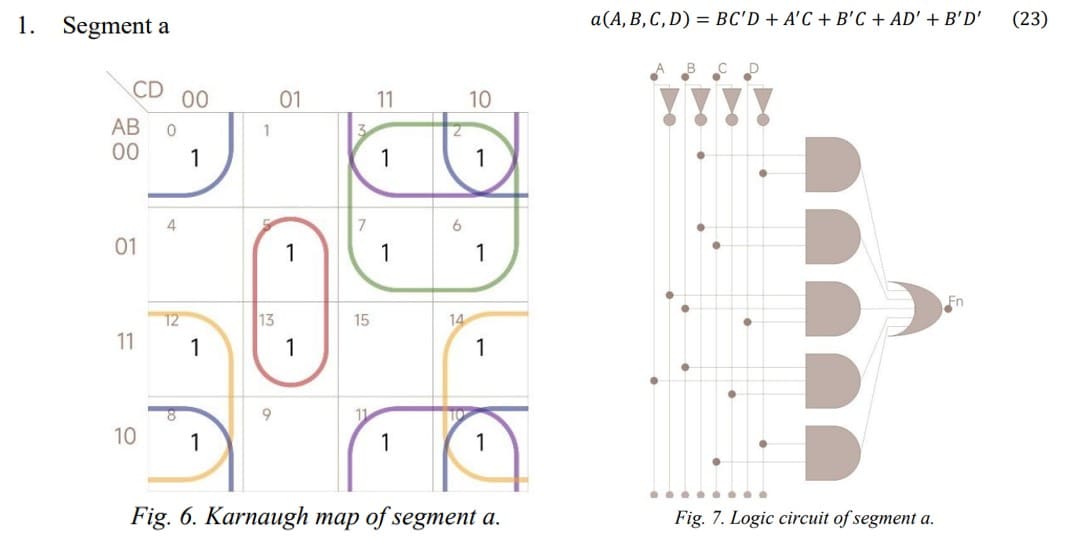
入力ビットの上の桁から順にABCDとして、カルノー図を書いてゴニョゴニョすると、
𝑎(𝐴, 𝐵, 𝐶, 𝐷) = 𝐵𝐶'𝐷 + 𝐴'𝐶 + 𝐵'𝐶 + 𝐴𝐷' + 𝐵'𝐷'このような論理式で変換できると言っています。「’」はNOT、かけ算はAND、足し算はORです。登場していませんが「⊕」がXORです。ただ、実はこの式は間違っているので(は?)後で訂正版を使います。

今度、カルノー図の使い方を教えてあげますね!@修士(工学)
セグメントa
では計算していきましょう。前回作った関数を使用します。
セグメントaの正しい論理式はこちらです。他にも等価な表記パターンがあるので、あくまで正しい論理式の一つと考えておきましょう。
segment a = C(B + A') + D'(A + B') + A'BD + AB'C'前回作ったNOT, AND, XOR, ORゲート関数を使って計算してみます。注意点として、A, B, C, DのそれぞれNOTである A’, B’, C’, D’ を先に用意しています。よく使うので。
#初期化
qc = QuantumCircuit(19)
#同時計算のため入力ビットを重ね合わせにする
qc.h(0)
qc.h(2)
qc.h(4)
qc.h(6)
#入力ビットの反転を用意しておく
NOT(0, 1) # A, A'
NOT(2, 3) # B, B'
NOT(4, 5) # C, C'
NOT(6, 7) # D, D'
#segment a = C(B + A') + D'(A + B') + A'BD + AB'C'
OR(2, 1, 8)
AND(4, 8, 9)
OR(0, 3, 10)
AND(7, 10, 11)
AND(1, 2, 12)
AND(12, 6, 13)
AND(0, 3, 14)
AND(14, 5, 15)
OR(9, 11, 16)
OR(16, 13, 17)
OR(17, 15, 18)
#計算
qc.measure_all()
backend = AerSimulator(method='matrix_product_state')
result = backend.run(qc, shots=500).result().get_counts()
#解の確認
pos = (0, 2, 4, 6, 18)
for i in range(2):
for j in range(2):
for k in range(2):
for l in range(2):
for r in result:
sel = ''.join(r[::-1][p] for p in pos)
if f'{i}{j}{k}{l}' == sel[:4]:
print(f'{sel} | {result[r]}/500')00001 | 40/500
00010 | 38/500
00101 | 25/500
00111 | 22/500
01000 | 25/500
01011 | 32/500
01101 | 34/500
01111 | 24/500
10001 | 38/500
10011 | 32/500
10101 | 28/500
10110 | 33/500
11001 | 39/500
11010 | 31/500
11101 | 28/500
11111 | 31/500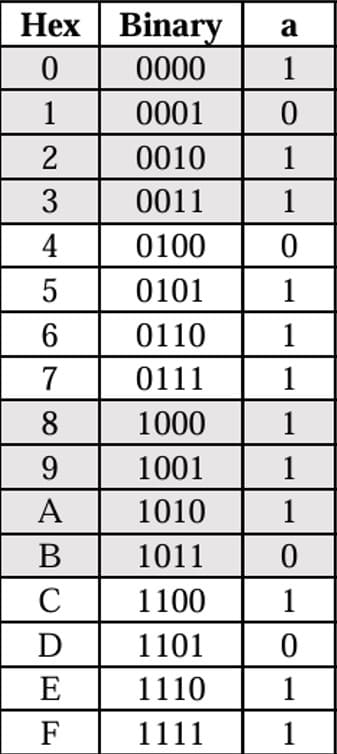
出力は左の4ビットが入力、右の1ビットが出力(セグメントa)です。表示順はソートしてあります。先程の表からセグメントa列だけ抜き出したのものと見比べてみると、16通りの入力に対して、出力はいずれも正しくなっていますね!素晴らしい!
なお、保存した量子譜がこちら。大きい。
セグメントb~g
他のセグメントもやっていきましょう。
セグメントb
構築したい論理式がこちら。
segment b = A'B' + B'D' + A'C'D' + D(A ⊕ C)XORを使わなくても表現できるのですが、使ったほうがゲートの数が減らせるらしい[要出典]
#初期化
qc = QuantumCircuit(17)
#同時計算のため入力ビットを重ね合わせにする
qc.h(0)
qc.h(2)
qc.h(4)
qc.h(6)
#入力ビットの反転を用意しておく
NOT(0, 1) # A, A'
NOT(2, 3) # B, B'
NOT(4, 5) # C, C'
NOT(6, 7) # D, D'
#segment b = A'B' + B'D' + A'C'D' + D(A ⊕ C)
AND(1, 3, 8)
AND(3, 7, 9)
AND(1, 5, 10)
AND(10, 7, 11)
XOR(0, 4, 12)
AND(6, 12, 13)
OR(8, 9, 14)
OR(14, 11, 15)
OR(15, 13, 16)
#計算
qc.measure_all()
backend = AerSimulator(method='matrix_product_state')
result = backend.run(qc, shots=500).result().get_counts()
#解の確認
pos = (0, 2, 4, 6, 16)
for i in range(2):
for j in range(2):
for k in range(2):
for l in range(2):
for r in result:
sel = ''.join(r[::-1][p] for p in pos)
if f'{i}{j}{k}{l}' == sel[:4]:
print(f'{sel} | {result[r]}/500')00001 | 35/500
00011 | 27/500
00101 | 26/500
00111 | 24/500
01001 | 28/500
01010 | 37/500
01100 | 32/500
01111 | 25/500
10001 | 31/500
10011 | 29/500
10101 | 24/500
10110 | 27/500
11000 | 35/500
11011 | 41/500
11100 | 32/500
11110 | 47/500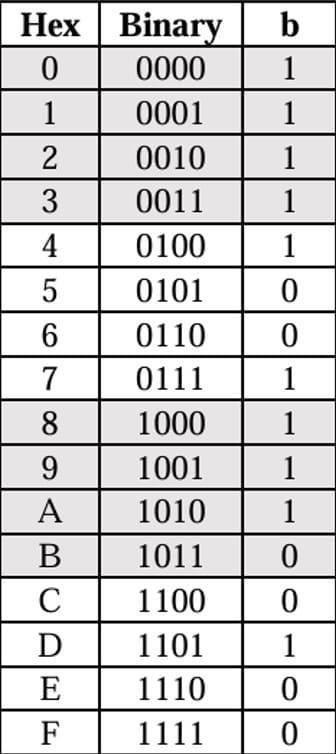
一致しています。
セグメントc
以下、差分だけ記載します。
#初期化
qc = QuantumCircuit(15)
#segment c = (A ⊕ B) + A'C' + A'D + C'D
XOR(0, 2, 8)
AND(1, 5, 9)
AND(1, 6, 10)
AND(5, 6, 11)
OR(8, 9, 12)
OR(12, 10, 13)
OR(13, 11, 14)
#解の確認
pos = (0, 2, 4, 6, 14)00001 | 20/500
00011 | 33/500
00100 | 40/500
00111 | 33/500
01001 | 29/500
01011 | 33/500
01101 | 31/500
01111 | 45/500
10001 | 30/500
10011 | 29/500
10101 | 19/500
10111 | 37/500
11000 | 32/500
11011 | 32/500
11100 | 28/500
11110 | 29/500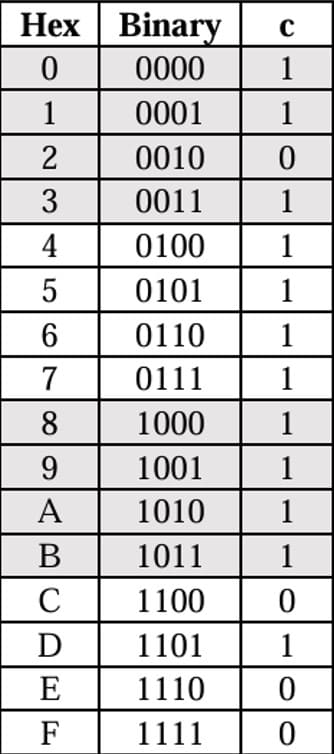
セグメントd
以下、差分だけ記載します。
#初期化
qc = QuantumCircuit(20)
#segment d = AC' + A'B'D' + B(C ⊕ D) + C(B'D + A'D')
AND(0, 5, 8)
AND(1, 3, 9)
AND(9, 7, 10)
XOR(4, 6, 11)
AND(2, 11, 12)
AND(3, 6, 13)
AND(1, 7, 14)
OR(13, 14, 15)
AND(4, 15, 16)
OR(8, 10, 17)
OR(17, 12, 18)
OR(18, 16, 19)
#解の確認
pos = (0, 2, 4, 6, 19)00001 | 38/500
00010 | 26/500
00101 | 31/500
00111 | 42/500
01000 | 31/500
01011 | 26/500
01101 | 31/500
01110 | 37/500
10001 | 22/500
10011 | 34/500
10100 | 34/500
10111 | 37/500
11001 | 28/500
11011 | 31/500
11101 | 24/500
11110 | 28/500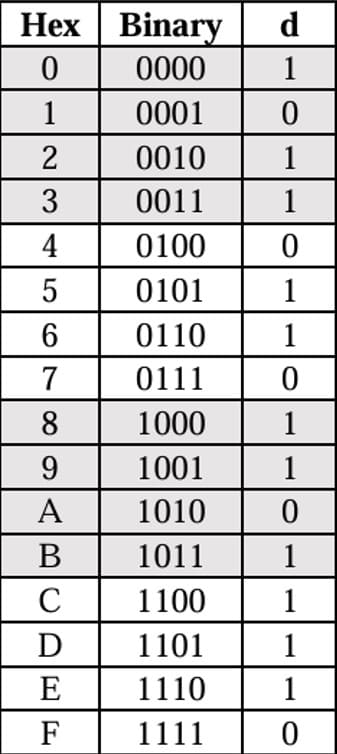
セグメントe
eは比較的単純なもよう。
#初期化
qc = QuantumCircuit(13)
#segment e = A(B + C) + D'(B' + C)
OR(2, 4, 8)
AND(0, 8, 9)
OR(3, 4, 10)
AND(7, 10, 11)
OR(9, 11, 12)
#解の確認
pos = (0, 2, 4, 6, 12)00001 | 40/500
00010 | 38/500
00101 | 30/500
00110 | 29/500
01000 | 31/500
01010 | 33/500
01101 | 30/500
01110 | 33/500
10001 | 23/500
10010 | 33/500
10101 | 28/500
10111 | 25/500
11001 | 35/500
11011 | 29/500
11101 | 34/500
11111 | 29/500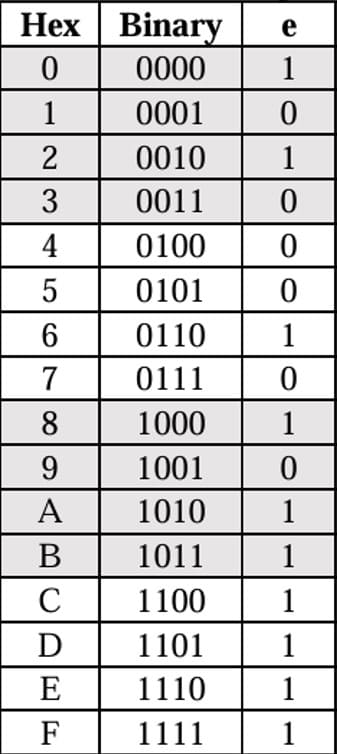
セグメントf
#初期化
qc = QuantumCircuit(19)
#segment f = D'(A + B + C') + AD(B' + C) + A'BC'D
OR(0, 2, 8)
OR(8, 5, 9)
AND(7, 9, 10)
OR(3, 4, 11)
AND(0, 6, 12)
AND(11, 12, 13)
AND(1, 2, 14)
AND(14, 5, 15)
AND(15, 6, 16)
OR(10, 13, 17)
OR(17, 16, 18)
#解の確認
pos = (0, 2, 4, 6, 18)00001 | 22/500
00010 | 38/500
00100 | 27/500
00110 | 33/500
01001 | 33/500
01011 | 32/500
01101 | 33/500
01110 | 48/500
10001 | 25/500
10011 | 31/500
10101 | 27/500
10111 | 32/500
11001 | 29/500
11010 | 30/500
11101 | 35/500
11111 | 25/500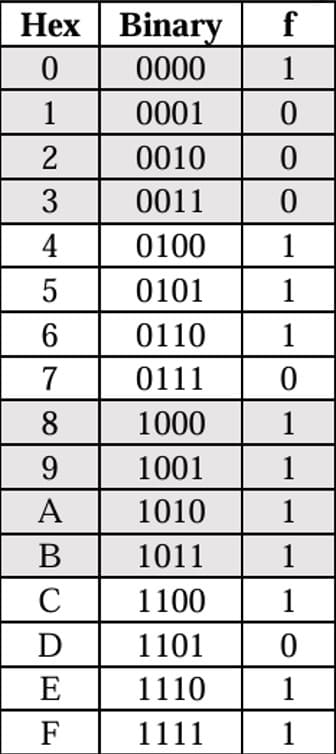
セグメントg
#初期化
qc = QuantumCircuit(16)
#segment g = A(B' + D) + C(B' + D') + A'BC'
OR(3, 6, 8)
AND(0, 8, 9)
OR(3, 7, 10)
AND(4, 10, 11)
AND(1, 2, 12)
AND(12, 5, 13)
OR(9, 11, 14)
OR(14, 13, 15)
#解の確認
pos = (0, 2, 4, 6, 15)00000 | 32/500
00010 | 23/500
00101 | 33/500
00111 | 25/500
01001 | 38/500
01011 | 33/500
01101 | 24/500
01110 | 30/500
10001 | 33/500
10011 | 39/500
10101 | 35/500
10111 | 31/500
11000 | 21/500
11011 | 36/500
11101 | 38/500
11111 | 29/500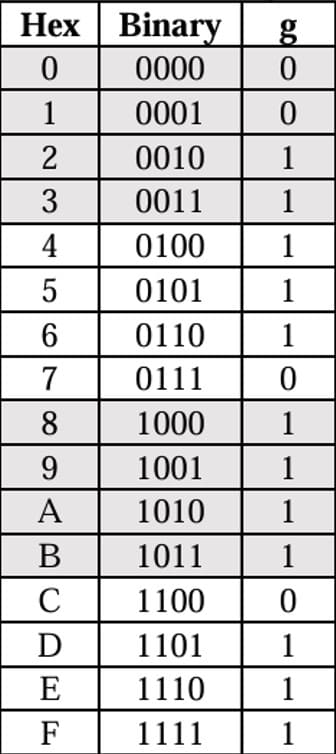
これですべてのセグメントの計算がうまくいきました!これで準備OKです。
おわりに
いや、何これ?量子コンピュータのやり方あってます??
とりあえず次回も読んでください。きっと感動すると思います。
2025/12/03追記
Google Colabで試せます↓(入力とNOT線の並びだけ少し違うのでご注意を)