AI要約
量子ゲートで7セグメントLEDを作るシリーズの第3弾。各セグメントの点灯ロジックを統合し、入力された数字に応じて7つのセグメントが正しく点灯する量子回路を構築しました。
やること
前回は7セグメントLEDの各セグメントの量子譜を実現しました。大変でしたね~^^;
今回は7つのセグメントを統合して、16通りの入力に対するLEDの出力を見てみます。ドキドキしますね!

セグメント統合
前回、入力からセグメントaを計算するのに使用した量子ビットの数は、入力が4個、入力の各NOTが4個、途中計算用が10個、出力が1個の合計19個でした。このうち入力関連の8個は他のセグメントでも使い回しますが、各セグメントの途中計算用が積み重なるので大量になりますね。何個になるか分かりません。
では、セグメントb以降の量子ビットの添字を書き換えて統合してみます。コードが長い!
#初期化
qc = QuantumCircuit(71)
#同時計算のため入力ビットを重ね合わせにする
qc.h(0)
qc.h(2)
qc.h(4)
qc.h(6)
#入力ビットの反転を用意しておく
NOT(0, 1) # A, A'
NOT(2, 3) # B, B'
NOT(4, 5) # C, C'
NOT(6, 7) # D, D'
#segment a = C(B + A') + D'(A + B') + A'BD + AB'C'
OR(2, 1, 8)
AND(4, 8, 9)
OR(0, 3, 10)
AND(7, 10, 11)
AND(1, 2, 12)
AND(12, 6, 13)
AND(0, 3, 14)
AND(14, 5, 15)
OR(9, 11, 16)
OR(16, 13, 17)
OR(17, 15, 18)
#segment b = A'B' + B'D' + A'C'D' + D(A ⊕ C)
AND(1, 3, 19)
AND(3, 7, 20)
AND(1, 5, 21)
AND(21, 7, 22)
XOR(0, 4, 23)
AND(6, 23, 24)
OR(19, 20, 25)
OR(25, 22, 26)
OR(26, 24, 27)
#segment c = (A ⊕ B) + A'C' + A'D + C'D
XOR(0, 2, 28)
AND(1, 5, 29)
AND(1, 6, 30)
AND(5, 6, 31)
OR(28, 29, 32)
OR(32, 30, 33)
OR(33, 31, 34)
#segment d = AC' + A'B'D' + B(C ⊕ D) + C(B'D + A'D')
AND(0, 5, 35)
AND(1, 3, 36)
AND(36, 7, 37)
XOR(4, 6, 38)
AND(2, 38, 39)
AND(3, 6, 40)
AND(1, 7, 41)
OR(40, 41, 42)
AND(4, 42, 43)
OR(35, 37, 44)
OR(44, 39, 45)
OR(45, 43, 46)
#segment e = A(B + C) + D'(B' + C)
OR(2, 4, 47)
AND(0, 47, 48)
OR(3, 4, 49)
AND(7, 49, 50)
OR(48, 50, 51)
#segment f = D'(A + B + C') + AD(B' + C) + A'BC'D
OR(0, 2, 52)
OR(52, 5, 53)
AND(7, 53, 54)
OR(3, 4, 55)
AND(0, 6, 56)
AND(55, 56, 57)
AND(1, 2, 58)
AND(58, 5, 59)
AND(59, 6, 60)
OR(54, 57, 61)
OR(61, 60, 62)
#segment g = A(B' + D) + C(B' + D') + A'BC'
OR(3, 6, 63)
AND(0, 63, 64)
OR(3, 7, 65)
AND(4, 65, 66)
AND(1, 2, 67)
AND(67, 5, 68)
OR(64, 66, 69)
OR(69, 68, 70)
#計算
qc.measure_all()
backend = AerSimulator(method='matrix_product_state')
result = backend.run(qc, shots=500).result().get_counts()
#解の確認
import matplotlib.pyplot as plt
pos = (0, 2, 4, 6, 18, 27, 34, 46, 51, 62, 70)
for i in range(2):
for j in range(2):
for k in range(2):
for l in range(2):
for r in result:
sel = ''.join(r[::-1][p] for p in pos)
if f'{i}{j}{k}{l}' == sel[:4]:
print(f'{sel} | {result[r]}')
#セグメント表示
plt.figure(figsize=(2, 2))
if sel[4] == '1':
plt.plot([0, 1], [2, 2], '-k', linewidth=5)
if sel[5] == '1':
plt.plot([1, 1], [1, 2], '-k', linewidth=5)
if sel[6] == '1':
plt.plot([1, 1], [0, 1], '-k', linewidth=5)
if sel[7] == '1':
plt.plot([0, 1], [0, 0], '-k', linewidth=5)
if sel[8] == '1':
plt.plot([0, 0], [0, 1], '-k', linewidth=5)
if sel[9] == '1':
plt.plot([0, 0], [1, 2], '-k', linewidth=5)
if sel[10] == '1':
plt.plot([0, 1], [1, 1], '-k', linewidth=5)
plt.xlim(-1, 2)
plt.ylim(-0.5, 2.5)
plt.title(f'{sel[4:]}')
plt.show()
plt.close()
matplotlibのグラフでLEDディスプレイを再現してあります。グラフ上部の解は、左4ビットが入力、右7ビットが出力(各セグメント)です。どうでしょうか?
できてるやんけ^^
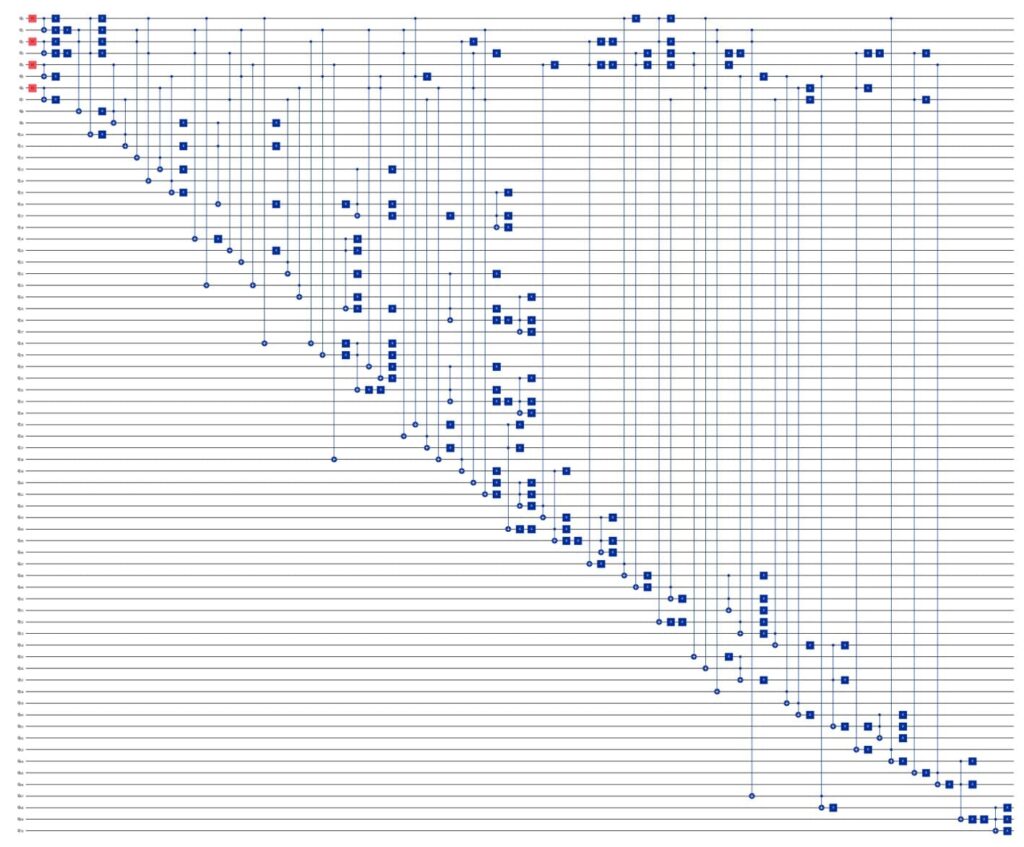
なお、量子譜の画像はこちら(クリックで拡大)(いや見えんわ!)。デカすぎる!
おわりに
シミュレーション上ではありますが、[0000] ~ [1111] の16通りの入力から7セグメントLEDを点灯させるための量子回路(量子譜)ができました!
このシリーズは一旦ここで休憩に入ります。今後は「量子譜の圧縮」や「電子部品で再現」をやろうと思っています。しばらくまた勉強してきますので、首をビヨンビヨンして待っていてください。
ほな、おやすみ ( ´⚰︎` )°゜
2025/12/03追記
Google Colabで試せます↓(入力とNOT線の並びだけ少し違うのでご注意を)

Google Colab