AI要約
量子ゲートで任意のピクセルアートを作るため、論理式を半自動で探索するツールを作りました。この方法の有効性を確かめるために新しいイラストをサクッと生成してしまいます。あと、使用する量子ビットも減らします。
はじめに
ネコを生成して完結したと思った!?
残念!まだ擦り続けます。
どんなイラストも生成できるように論理式の半自動探索ツールを作りました。論理王におれはなる!(倒置法)あと、使用する量子ビットも減らします。
論理式の自動探索
ネコの画像を再掲します↓
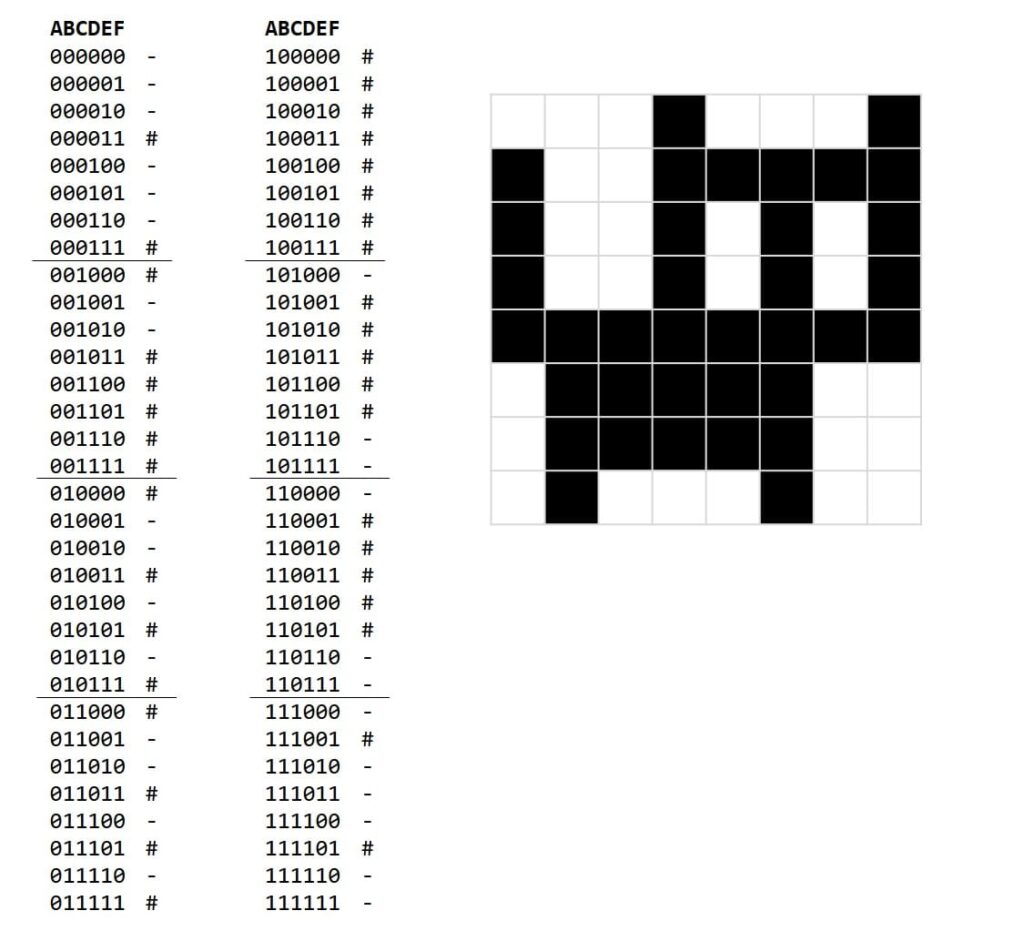
やはり6ビットの論理合成を自力で作るのは困難です。前回は一応できましたが、もっと効率的な式があるんだろうなと思うと夜も眠れません。
そこで、Pythonで「6ビット論理式半自動探索ツール」なるものを作りました。未公開です。
探索したいピクセルアートを入力すると、いくつかの段階に分けて候補式を提示してくれます。
#入力(ネコ)
img = ['00010001',
'10011111',
'10010101',
'10010101',
'11111111',
'01111100',
'01111100',
'01000100']次の4パターンの式を全探索して、目的イラストの構成部品になり得るものを提示してくれます。
![]()
![]()
![]()
![]()
※ X は X’ (NOT X) も含む
※ + (OR) は ⊕ (XOR) も含む
第1段階は2つの文字からなる式(1アクションで到達できる式)ですが、これは基本的に該当なし。
第2段階(2アクション式)で次の2候補が出ました。
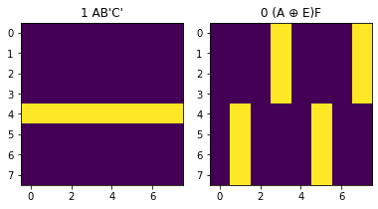
第3段階(3アクション式)は24候補出ました。一部を掲載します。
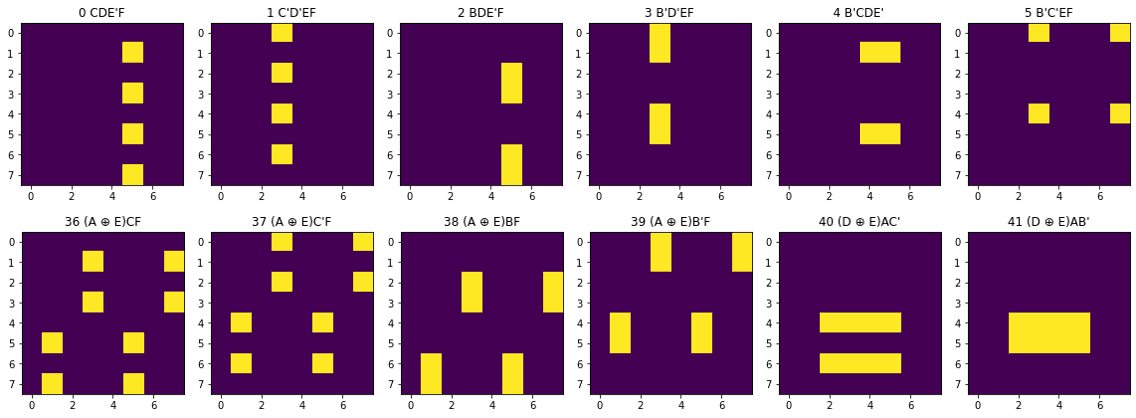
ここまでに出た式をフル活用してもまだイラストが埋まらないので、第4段階まで見て適当な部品を選びます。選ぶのは人間がやります。
結果、キミに決めた!
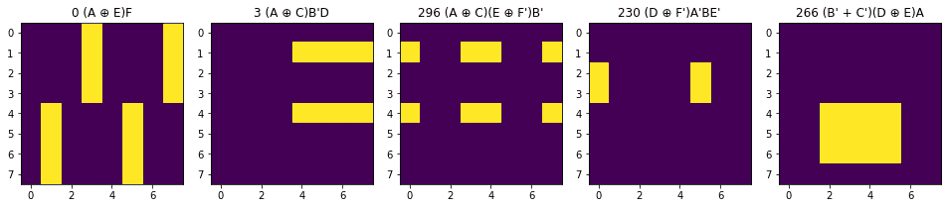
#新ネコ
(A ⊕ E)F
(A ⊕ C)B'D
(A ⊕ C)(E ⊕ F')B'
(D ⊕ F')A'BE'
(B' + C')(D ⊕ E)A人力では絶対に思いつかないような式がありますね~ φ(´・ω・`)スゲー
参考までに、前回私が作った式はこちらです。

#旧ネコ
AB'C'
A'EF
(A + D)(B + C)E'F
A'(B + C)D'E'F'
A(B ⊕ C)(D ⊕ E)
A'B'CD前回は6式だったのが、今回は5式に削減できています。
この論理式は出来損ないだ。食べられないよ(27♂ 新聞社)
まさにこういう気分です。
量子ビットの節約
もう一つ工夫してみます。これまでは途中式が出る度に新品の量子ビットを使っていたので36量子ビットまで膨らんでいました(それでも少ないほうですが)。
調べてみると、不要になったものは
qc.reset()で0に初期化できるようなので、途中式用の量子ビットはこれで再利用していきます。
さらに、D’ (NOT D) は使用しないのでそもそも作らないことにします。
これらを反映したコードがこちらです。
#初期化
qc = QuantumCircuit(20)
#6ビット(64通り)の乱数を作る
qc.h(0) # A
qc.h(1) # B
qc.h(2) # C
qc.h(3) # D
qc.h(4) # E
qc.h(5) # F
#便利のため、各NOTを用意
NOT(0, 6) # A'
NOT(1, 7) # B'
NOT(2, 8) # C'
# D'
NOT(4, 9) # E'
NOT(5, 10) # F'
#11, 12, 13を途中式用にする
#ブロック1
XOR(0, 4, 11) # (A ⊕ E)
AND(11, 5, 14) # (A ⊕ E)F
#ブロック2
qc.reset(11)
XOR(0, 2, 11) # (A ⊕ C)
AND(11, 7, 12) # (A ⊕ C)B'
AND(12, 3, 15) # (A ⊕ C)B'D
#ブロック3
qc.reset(11)
XOR(4, 10, 11) # (E ⊕ F')
AND(12, 11, 16) # (A ⊕ C)(E ⊕ F')B'
#ブロック4
qc.reset(11)
qc.reset(12)
XOR(3, 10, 11) # (D ⊕ F')
AND(11, 6, 12) # (D ⊕ F')A'
AND(12, 1, 13) # (D ⊕ F')A'B
AND(13, 9, 17) # (D ⊕ F')A'BE'
#ブロック5
qc.reset(11)
qc.reset(12)
qc.reset(13)
OR(7, 8, 11) # (B' + C')
XOR(3, 4, 12) # (D ⊕ E)
AND(11, 12, 13) # (B' + C')(D ⊕ E)
AND(13, 0, 18) # (B' + C')(D ⊕ E)A
#塗るかどうかの総合判定ビット
qc.reset(11)
qc.reset(12)
qc.reset(13)
OR(14, 15, 11)
OR(11, 16, 12)
OR(12, 17, 13)
OR(13, 18, 19)「(A ⊕ C)B’」は再利用しています。再利用も考慮してあえて長い式を選択する戦略もあるんですよね。完全自動探索ツールにするならそこまで考慮したいですね。
ということで、なんと20量子ビットまで減らせました。サンプリングすると問題なくネコが生成されました。
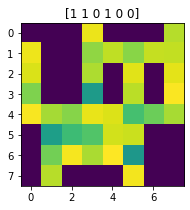
量子譜はかつてなくコンパクトになっています。
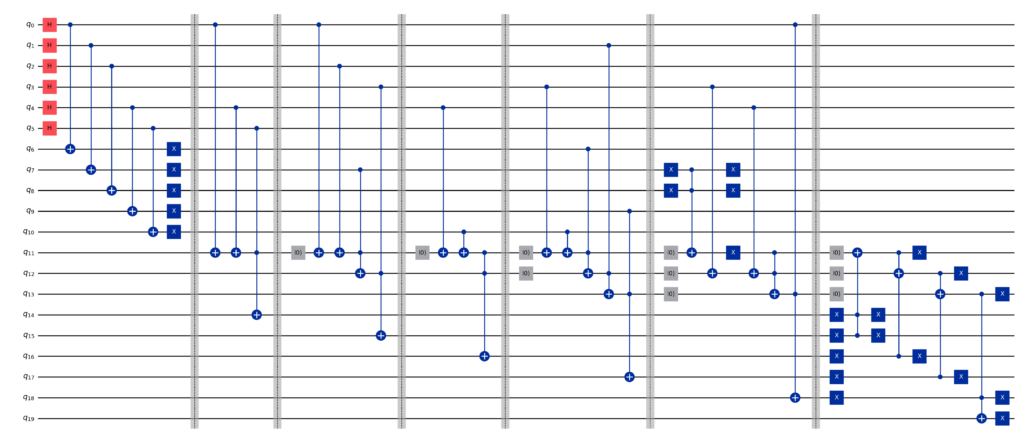
他のイラストもできる?
せっかく半自動探索ツールを作ったので他のイラストも生成してみましょう。こちらの「心」に挑戦します。

探索の結果、こちらの式たちに決定。
#心
AB'D'E'F'
(A ⊕ B)D'EF'
(A + F)BCDE'
(A ⊕ F')B'CDE
(A ⊕ D')(C ⊕ E)BF'
(A ⊕ D)(E ⊕ F')BC'
いやキモすぎる。。
誰が思いつくんだ。XOR使いすぎだろ!
コードはこんな感じ。たったの22量子ビット。「D’F’」「CD」は再利用しています。
#初期化
qc = QuantumCircuit(22)
#6ビット(64通り)の乱数を作る
qc.h(0) # A
qc.h(1) # B
qc.h(2) # C
qc.h(3) # D
qc.h(4) # E
qc.h(5) # F
#便利のため、各NOTを用意
# A'
NOT(1, 6) # B'
NOT(2, 7) # C'
NOT(3, 8) # D'
NOT(4, 9) # E'
NOT(5, 10) # F'
#11, 12, 13, 14を途中式用にする
#ブロック1
AND(0, 6, 11) # AB'
AND(11, 9, 12) # AB'E'
AND(8, 10, 13) # D'F'
AND(12, 13, 15) # AB'D'E'F'
#ブロック2
qc.reset(11)
qc.reset(12)
XOR(0, 1, 11) # (A ⊕ B)
AND(11, 4, 12) # (A ⊕ B)E
AND(12, 13, 16) # (A ⊕ B)D'EF'
#ブロック3
qc.reset(11)
qc.reset(12)
qc.reset(13)
OR(0, 5, 11) # (A + F)
AND(11, 1, 12) # (A + F)B
AND(12, 9, 13) # (A + F)BE'
AND(2, 3, 14) # CD
AND(13, 14, 17) # (A + F)BCDE'
#ブロック4
qc.reset(11)
qc.reset(12)
qc.reset(13)
XOR(0, 10, 11) # (A ⊕ F')
AND(11, 6, 12) # (A ⊕ F')B'
AND(12, 4, 13) # (A ⊕ F')B'E
AND(13, 14, 18) # (A ⊕ F')B'CDE
#ブロック5
qc.reset(11)
qc.reset(12)
qc.reset(13)
qc.reset(14)
XOR(0, 8, 11) # (A ⊕ D')
XOR(2, 4, 12) # (C ⊕ E)
AND(11, 12, 13) # (A ⊕ D')(C ⊕ E)
AND(13, 1, 14) # (A ⊕ D')(C ⊕ E)B
AND(14, 10, 19) # (A ⊕ D')(C ⊕ E)BF'
#ブロック6
qc.reset(11)
qc.reset(12)
qc.reset(13)
qc.reset(14)
XOR(0, 3, 11) # (A ⊕ D)
XOR(4, 10, 12) # (E ⊕ F')
AND(11, 12, 13) # (A ⊕ D)(E ⊕ F')
AND(13, 1, 14) # (A ⊕ D)(E ⊕ F')B
AND(14, 7, 20) # (A ⊕ D)(E ⊕ F')BC'
#塗るかどうかの総合判定ビット
qc.reset(11)
qc.reset(12)
qc.reset(13)
qc.reset(14)
OR(15, 16, 11)
OR(11, 17, 12)
OR(12, 18, 13)
OR(13, 19, 14)
OR(14, 20, 21)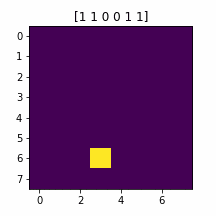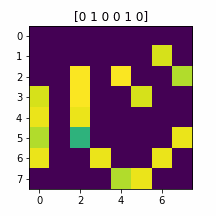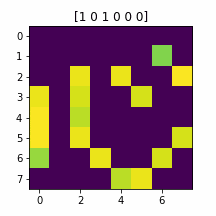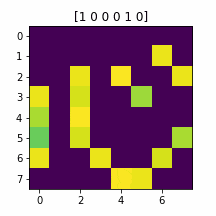
量子譜もやっぱりコンパクト
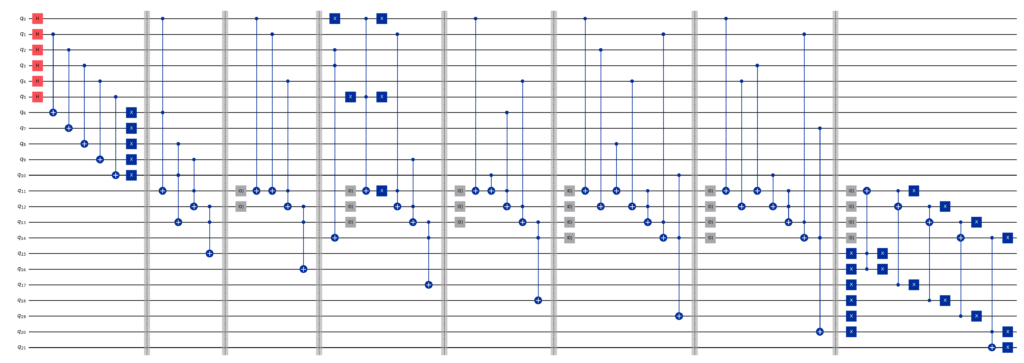
大成功です!
おわりに
このシリーズを書くのも最後かのぅ (´・ω・`)

本業の最適化案件で部屋に缶詰になっているせいか、アニメネタが多くなってしまいました(は?)


