やること
葉脈ってきれいですよね。フラクタル構造で葉の隅々まで水を運んでいるように見えます。

今回はプログラムで葉脈を作ってみます。このようなフラクタルな構造を作るには再帰的処理が有効です。再帰的な関数はざっくり言うと「自分で自分を呼び出す関数」です。子分を作って、子分もまた子分を作って・・・というようにねずみ講 MLM(マルチレベルマーケティング)のように子分が増えていくイメージですね。
実行環境
WinPython3.6をおすすめしています。
WinPython - Browse /WinPython_3.6/3.6.7.0 at SourceForge.net
Portable Scientific Python 2/3 32/64bit Distribution for Windows
Google Colaboratoryが利用可能です。

Google Colab
コード
まずは1本目の線を斜めに描いておきます。
import cv2
import numpy as np
import matplotlib.pyplot as plt
#画像表示関数
def show(img):
plt.imshow(img, vmin=0, vmax=255)
plt.show()
#サイズ
size = 512
#初期化(画像はこの後ずっとグローバル参照される)
img = np.zeros((size, size))
#1本目
start = np.array([0, 0])
end = np.array([size, size])
cv2.line(img, tuple(start), tuple(end), 255, 2)
show(img)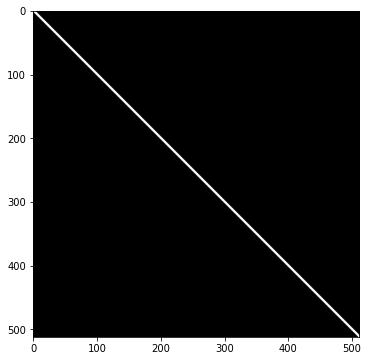
再帰的に枝を追加する関数を用意して実行してみましょう。この関数は受け渡された枝(始点と終点)の中点から左右に60°分岐した2本の枝を画像に書き込みます。そして2本の枝に対してまたこの関数で子どもの枝を生成させます。無限に続くといけないので指定した深さで止めます。
#枝を追加する関数
def add_branch(start, end, depth):
#スタートとエンドの中点
middle = (start + end) / 2
print(middle)
#回転行列
t1 = np.deg2rad(60)
R1 = np.array([[np.cos(t1), -np.sin(t1)],
[np.sin(t1), np.cos(t1)]])
t2 = np.deg2rad(-60)
R2 = np.array([[np.cos(t2), -np.sin(t2)],
[np.sin(t2), np.cos(t2)]])
#新しい枝のベクトル
vec = (end - middle) * 0.7 #少し短くしておく
vec1 = np.dot(R1, vec)
vec2 = np.dot(R2, vec)
#各点をintにしておく
middle = middle.astype(int)
vec1 = vec1.astype(int)
vec2 = vec2.astype(int)
#新しい枝の書き込み
cv2.line(img, tuple(middle), tuple(middle + vec1), 255, 2)
cv2.line(img, tuple(middle), tuple(middle + vec2), 255, 2)
#現在の深さ
current_depth = depth + 1
#深さが足りなければ再帰的に実行
if current_depth < stop_depth:
add_branch(middle, middle + vec1, depth=current_depth)
add_branch(middle, middle + vec2, depth=current_depth)
#深さ
stop_depth = 1
#再帰的な枝の追加
add_branch(start, end, depth=0)
show(img)[256. 256.]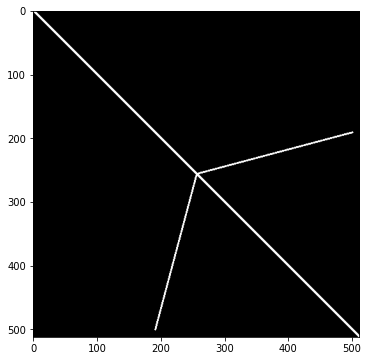
子どもの枝が書き込まれました。深さ1なので1回子どもが生まれたら終了です。
深さを4にすると、
[256. 256.]
[223.5 378. ]
[180.5 389. ]
[169.5 378.5]
[176. 403.5]
[254. 409.]
[250.5 423.5]
[268.5 405.5]
[378. 223.5]
[409. 254.]
[405.5 268.5]
[423.5 250.5]
[389. 180.5]
[403.5 176. ]
[378.5 169.5]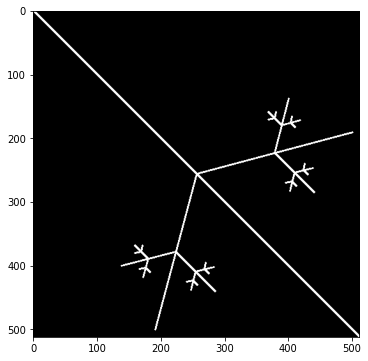
いいですね、うまくいきました。
おまけ:葉脈の複雑さによる水の浸透シミュレーション
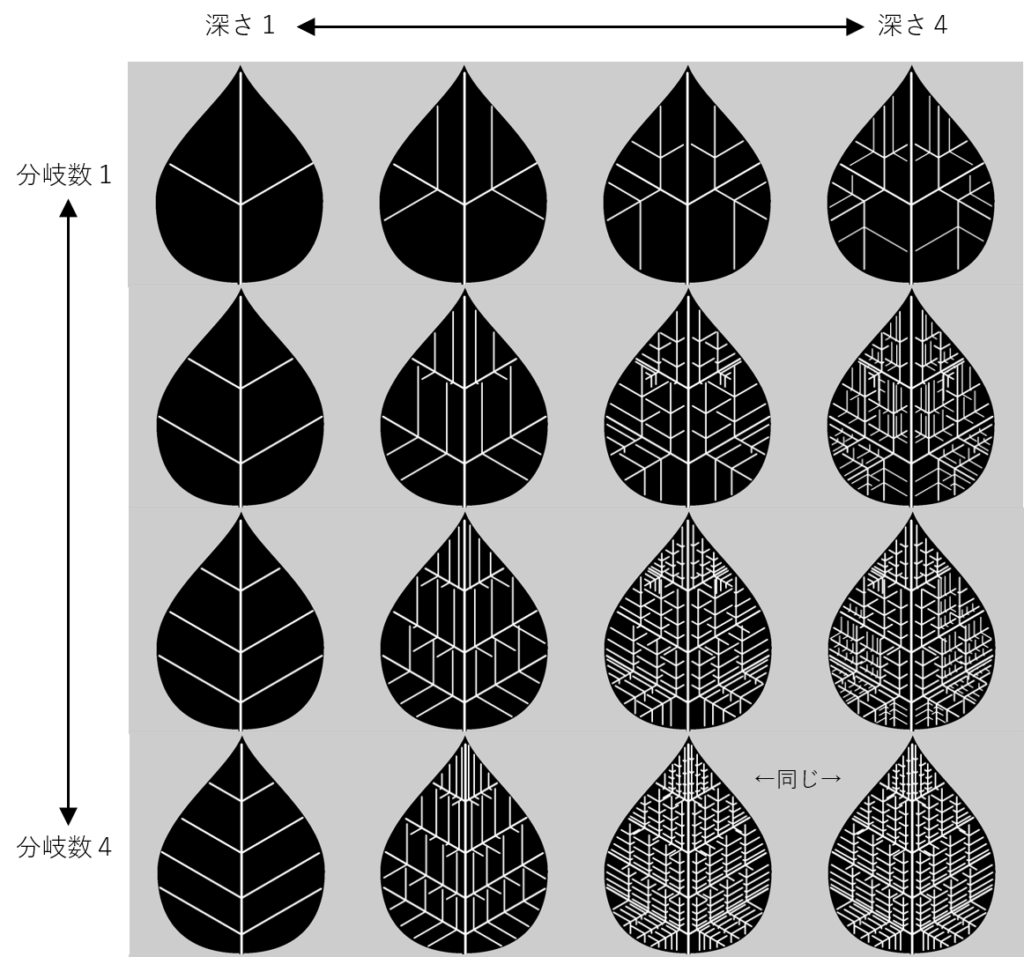
これを使ってさまざまな複雑さの葉脈を作ってみました。それゆけ網状脈!
葉柄からの水の浸透をシミュレーションしました。こちらの写真は桑の葉に蛍光液を吸わせたものです。(桑かな?)

2次元セルオートマトン的に畳み込み更新を繰り返しました。葉脈は葉肉に対して30倍の浸透速度にしてあります。4K画質でどうぞ。
分岐数や深さが大きいほど水が葉全体に速く行き渡るのが分かりますね。
おわりに
ところでHaskell(プログラミング言語)は再帰処理の訓練に良いと聞きました。これも勉強してみましょうか。