やること
ダーツの「カウントアップ」は、24本投げて合計得点を競う遊び方です。
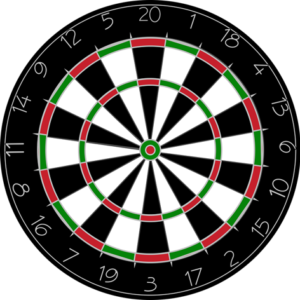
ど真ん中の赤い部分をインナーブル(50点)、その周りの緑の部分をアウターブル(25点)と呼び、それ以外はボードの縁に書かれている得点(シングル)が与えられます。ただし、中程にある細い帯状の領域に刺されば3倍(トリプル)、外側の帯に刺されば2倍(ダブル)となります。
さて、上級者はひたすら20トリプル(=60点)を狙うのですが、初心者はあんな細いところ狙えません。しかも1点と5点に挟まれているので悲惨なことになります。
初心者向けの戦略として、「練習あるのみ、ブルを狙え!」「横ブレを抑えて20トリプルを狙え!」「16~19のエリアは期待値が高い!」といったアドバイスがされることがありますが、本当に正しいでしょうか。
今回はモンテカルロ法を用いて、個人の縦ブレと横ブレの規模に応じた最適戦略を調べてみます。
参考文献
モンテカルロ法とは、ある値や確率が知りたいときに、コンピュータ内でサイコロを振りまくって実験的に求める方法です。今回はコンピュータ内でダーツを投げまくって期待値を調べます。
実行環境
WinPython3.6をおすすめしています。
Google Colaboratoryが利用可能です。

import
必要なパッケージをインポートします。
import math
import numpy as np
import numpy.random as nr
import matplotlib.pyplot as pltパラメータと設定
よこ方向のブレ(mm単位の標準偏差)、たて方向のブレ(mm単位の標準偏差)、各座標めがけて何回投げるか、を設定します。ちなみに標準偏差2mmというのは、だいたい「2/3の確率で±2mmの範囲に収まる」くらいのブレですので、超上級者だと思います。Phil Taylorおじさんをご存知ですか?
#===========================
# パラメータ
#===========================
#投げたときのブレ具合(標準偏差、単位:mm)
sd_x = 2 #よこ方向
sd_y = 2 #たて方向
#各座標狙って何回投げるか(多いほうが力こそパワー)
num = 50
#===========================
# 設定
#===========================
#スコア一覧
score_set = [6, 13, 4, 18, 1, 20, 5, 12, 9, 14, 11, 8, 16, 7, 19, 3, 17, 2, 15, 10]関数たち
(x, y)座標から(r, degree)を返す関数、(r, degree)からスコアを返す関数を作ります。つまり、ある(x, y)座標に刺さったときに何点もらえるのかを調べる関数セットです。
ボードはソフトダーツのサイズを用いました。(厳密な規格はないそうですが)
#===========================
# 関数
#===========================
#(x, y)座標から(r, degree)を返す
def xy2rd(x, y):
#中心からの距離
r = (x**2 + y**2)**0.5
#角度(3時から上へ)
rad = math.atan2(y, x)
degree = math.degrees(rad)
return r, degree
#(r, degree)からスコアを返す
def score(r, degree):
#アウトの場合
if 197 < r:
return 0
#ブル系の場合
if r < 8:
return 50
elif r < 22:
return 25
#基本スコア
index = int((degree + 9) // 18)
score = score_set[index]
#ダブル、トリプル処理
if 105 < r <= 125:
return score * 3
if 177 < r <= 197:
return score * 2
return score
#関数チェック
print('座標(0, 110)を極座標へ:{}'.format(xy2rd(0, 110)))
print('中心から110mm, 3時から反時計回りに90度:{}'.format(score(110, 90)))座標(0, 110)を極座標へ:(110.0, 90.0)
中心から110mm, 3時から反時計回りに90度:60試しに (x, y) = (0, 110) を極座標に変換してスコアを調べてみると、60点(20トリプル)でした。極座標では「中心から110mm, 3時から反時計回りに90度」を意味します。
各座標めがけて50本ずつ投げて期待値を調べる
初期設定のとおり、たて・よこ共に標準偏差2mmのブレがある時の期待値グラフを出しました。
#===========================
# メイン
#===========================
#各座標の期待値を入れる配列
E = np.zeros((394, 394))
for i in range(394):
for j in range(394):
#目標座標
x, y = (j - 197, 197 - i) #対応ややこしい。(i, j)は0~393, (x, y)は-197~196
#ブレさせる
x_bure = nr.normal(x, sd_x, num)
y_bure = nr.normal(y, sd_y, num)
#ある座標の期待値
e = 0
for n in range(num):
#xy座標から極座標へ
r, degree = xy2rd(x_bure[n], y_bure[n])
#スコアを調べる
e += score(r, degree)
#ある座標の期待値を格納
e /= num
E[i, j] = e
#期待値最大の座標
best_x, best_y = np.unravel_index(np.argmax(E), E.shape)
#結果グラフ
plt.imshow(E, vmin=0, vmax=60)
plt.plot(best_y, best_x, 'or', markersize=10)
plt.show()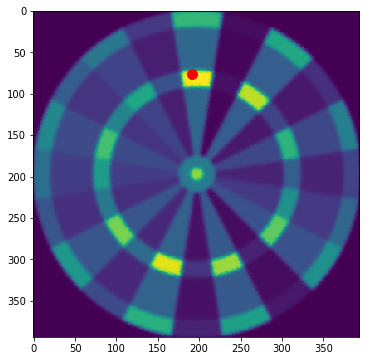
赤点はもっとも期待値が高かった座標を示しています。これだけの腕前があれば、20トリプルを狙うのがよいということです。
網羅的に調べた
たて・よこのブレをそれぞれ 2, 5, 10, 20, 40mm で動かしながら調べました。
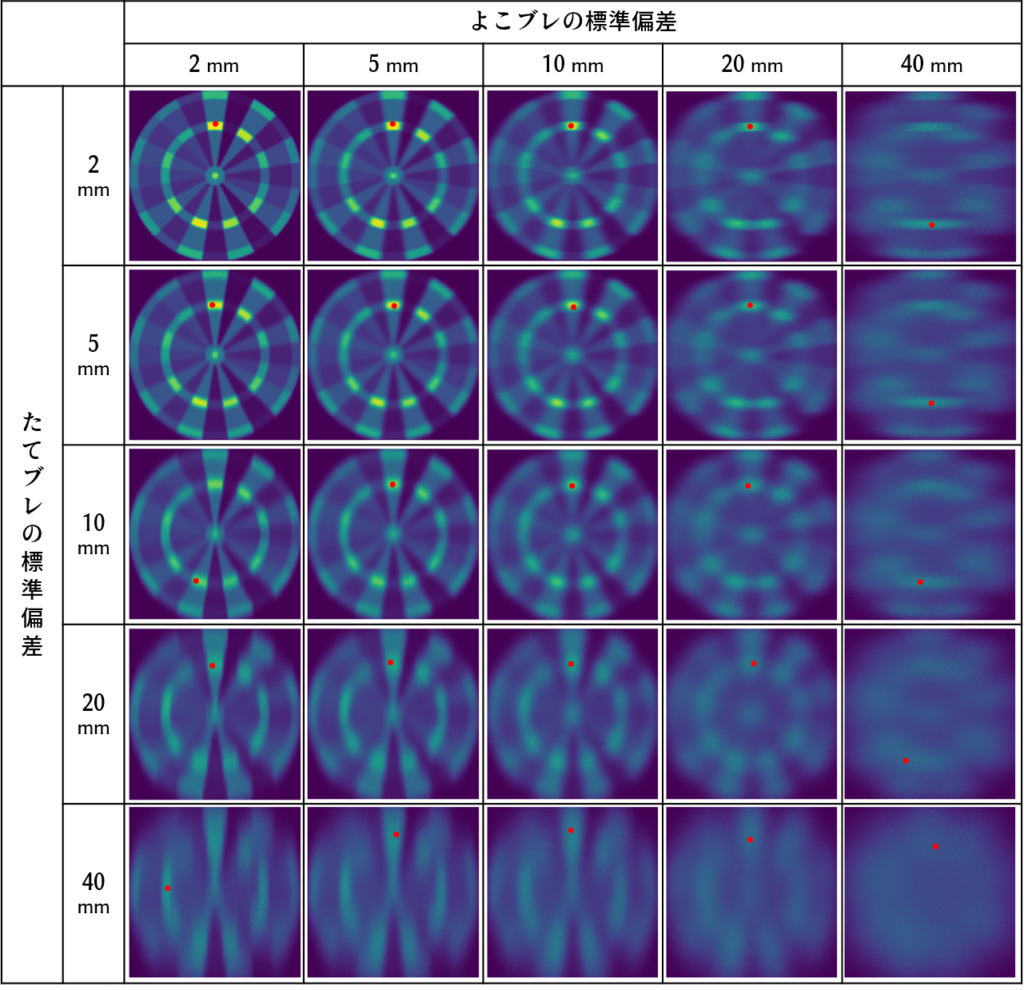
結局、どこを狙えば良いのかを整理しました。
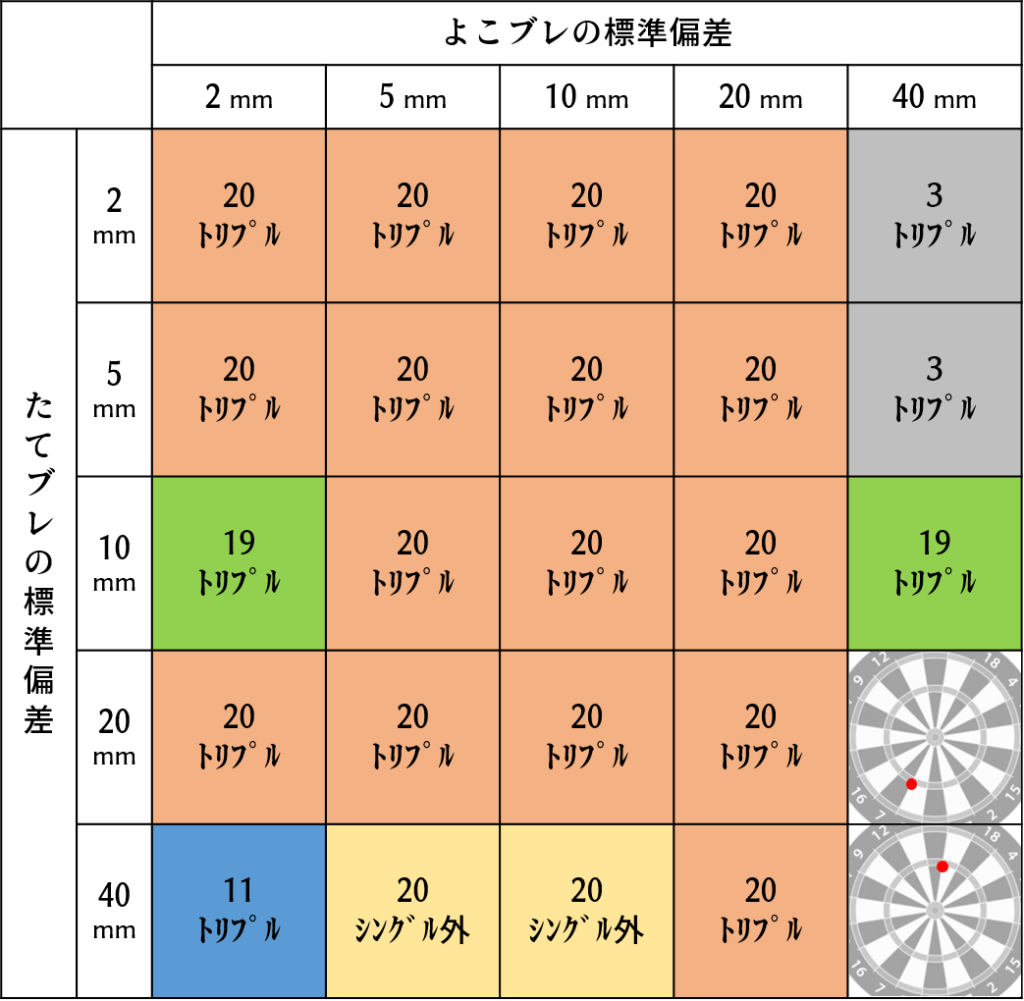
これを見ると、だいたい円状にブレる人は「20トリプルを狙っとけ」ですが、縦にブレやすい人は19トリプルや11トリプル、横にブレやすい人は3トリプルや19トリプルが最適戦略になり得るようです。
皆さんもとりあえず100本投げてブレの傾向を知り、モンテカルロ法を駆使して自分にあった戦略を見つけてみてはいかがでしょうか。

