やること
※2022/09/20修正があります
迷路の最短経路を求めたいです。例えば、「スタートから水を流す」ような探索方法を幅優先探索と呼びます。一方で、「スタートからルンバを発進させ、行き止まりにぶつかったら途中の分かれ道まで戻る」ような探索方法を深さ優先探索と呼びます。今回は、幅優先探索を実装してみましょう。
実行環境
WinPython3.6をおすすめしています。
WinPython - Browse /WinPython_3.6/3.6.7.0 at SourceForge.net
Portable Scientific Python 2/3 32/64bit Distribution for Windows
sourceforge.net
参考文献
迷路の探索アルゴリズムについては、とにかくこちらをご参照ください。なんかもうすごいです。
迷路で眺める探索アルゴリズム(Search algorithm visualize) | How wonderfl!!
fl.corge.net
import
今回使うパッケージをインポートします。
import numpy as np
import matplotlib.pyplot as plt
from scipy.ndimage.filters import minimum_filter, maximum_filter見慣れない関数（minimum_filter, maximum_filter）があります。これらは、深層学習で言うところの「Maxpooling / Minpooling」のような処理を実現してくれます。「周囲のマスで一番小さい数字を拾う」という処理で用いますが、詳細はまあ置いておきましょう。
迷路の作成
はい、手入力です。’#’は壁（＝障害物）です。
#########################
# 迷路
#########################
maze = ['----#-----',
'--#--#--#-',
'g--#---#s-']前処理
コスト、探索済みか？、障害物の２次元配列を用意します。
#########################
# 前処理
#########################
#たてとよこ
h, w = len(maze), len(maze[0])
#コスト
cost = np.zeros((h, w), dtype=int) + 999
#コストが書き込まれて探索が終了したマス（bool）
done = np.zeros((h, w), dtype=bool)
#障害物（bool）
barrier = np.zeros((h, w), dtype=bool)
#プーリング用のフィルタ
g = np.array([[0, 1, 0],
[1, 1, 1],
[0, 1, 0]])
#mazeからスタート位置、ゴール位置、障害物位置を取得
for i in range(h):
maze[i] = list(maze[i])
for j in range(w):
if maze[i][j] == 's':
start = (i, j)
cost[i, j] = 0
done[i, j] = True
if maze[i][j] == 'g':
goal = (i, j)
if maze[i][j] == '#':
barrier[i, j] = True
print('start\n{}'.format(start))
print('goal\n{}'.format(goal))
print('cost\n{}'.format(cost))
print('done\n{}'.format(done))
print('barrier\n{}'.format(barrier))start
(2, 8)
goal
(2, 0)
cost
[[999 999 999 999 999 999 999 999 999 999]
[999 999 999 999 999 999 999 999 999 999]
[999 999 999 999 999 999 999 999 0 999]]
done
[[False False False False False False False False False False]
[False False False False False False False False False False]
[False False False False False False False False True False]]
barrier
[[False False False False True False False False False False]
[False False True False False True False False True False]
[False False False True False False False True False False]]スタート位置とゴール位置が正しく検出されています。コスト配列はいわば進んだ距離で、スタート位置だけが０、その他のマスは999*が記録されています。探索済み配列は、スタート位置だけがTrueです。障害物配列は、障害物の位置がTrueです。
*はい、このコードは999ステップ以上には対応していません。
表示関数
ごにょごにょと書きます。引数は処理ステップ数です。
#########################
# 表示関数
#########################
def show(step):
plt.figure(figsize=(10, 10))
#フィールド、障害物の表示
plt.imshow(barrier, cmap='inferno_r')
#スタート、ゴールの記入
plt.text(start[1]-0.4, start[0]-0.1, 'S', size = 20, color = 'r')
plt.text(goal[1]-0.4, goal[0]-0.1, 'G', size = 20, color = 'b')
#コストの記入
x, y = np.where(cost != 999)
c = cost[x, y]
for i in range(len(x)):
plt.text(y[i]-0.1, x[i]+0.1, c[i], size = 20, color = 'gray')
#plt.savefig('save/{}.png'.format(step), bbox_inches='tight', pad_inches=0)
plt.show(), plt.close(), print()
#表示
show(0)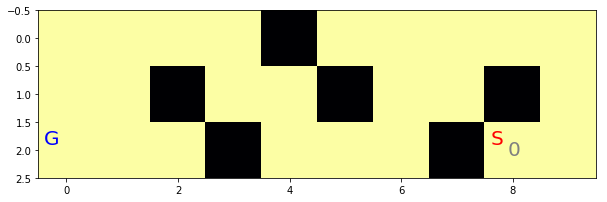
コスト配列のうち999でない数字がグレーで書き込まれます。
幅優先探索で迷路を探索する
水が次のステップでどこに流れ込むか、またそこへ行くためのコストはいくらか。これらを計算し、costとdoneの配列を更新します。気になる方はprintのコメントアウトを解除して見てみてください。
#########################
# 幅優先探索
#########################
for i in range(1, 999):
#次に進出するマスのbool
done_next = maximum_filter(done, footprint=g) * ~done
#print('done_next\n{}'.format(done_next))
#次に進出するマスのcost
cost_next = minimum_filter(cost, footprint=g) * done_next
cost_next[done_next] += 1
#print('cost_next\n{}'.format(cost_next))
#costを更新
cost[done_next] = cost_next[done_next]
#ただし障害物のコストは999とする
cost[barrier] = 999
#print('cost\n{}'.format(cost))
#探索終了マスを更新
done[done_next] = done_next[done_next]
#ただし障害物は探索終了としない
done[barrier] = False
#print('done\n{}'.format(done))
#表示
show(i)
#終了判定
if done[goal[0], goal[1]] == True:
break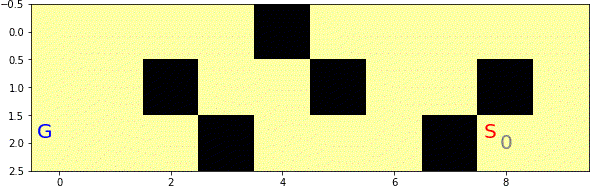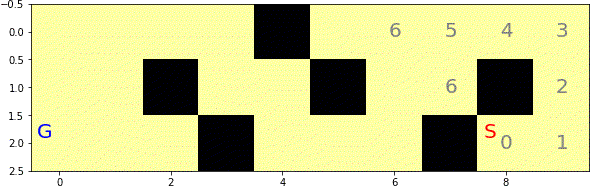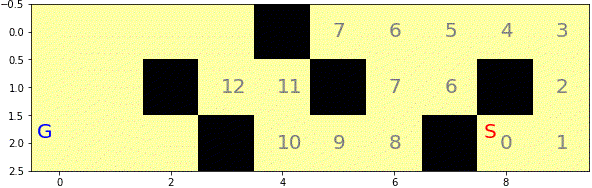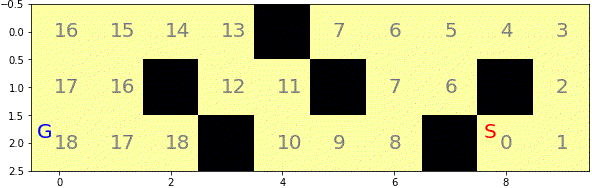
ルートのあぶり出し
※2022/09/20修正
このままでは最短ルートが分かりませんので、ゴールから逆にたどって調べます。
#########################
# ゴールから逆順でルート計算
#########################
point_now = goal
cost_now = cost[goal[0], goal[1]]
route = [goal]
print('route\n{}'.format(route))
while cost_now > 0:
#上から来た場合
if 0 <= point_now[0] - 1 and cost[point_now[0] - 1, point_now[1]] == cost_now - 1:
#更新
point_now = (point_now[0] - 1, point_now[1])
cost_now = cost_now - 1
#記録
route.append(point_now)
#下から来た場合
if point_now[0] + 1 < h and cost[point_now[0] + 1, point_now[1]] == cost_now - 1:
#更新
point_now = (point_now[0] + 1, point_now[1])
cost_now = cost_now - 1
#記録
route.append(point_now)
#左から来た場合
if 0 <= point_now[1] - 1 and cost[point_now[0], point_now[1] - 1] == cost_now - 1:
#更新
point_now = (point_now[0], point_now[1] - 1)
cost_now = cost_now - 1
#記録
route.append(point_now)
#右から来た場合
if point_now[1] + 1 < w and cost[point_now[0], point_now[1] + 1] == cost_now - 1:
#更新
point_now = (point_now[0], point_now[1] + 1)
cost_now = cost_now - 1
#記録
route.append(point_now)
#ルートを逆順にする
route = route[::-1]
print('route\n{}'.format(route))route
[(2, 0)]
route
[(2, 8), (2, 9), (1, 9), (0, 9), (0, 8), (0, 7), (1, 7), (1, 6), (2, 6), (2, 5), (2, 4), (1, 4), (1, 3), (0, 3), (0, 2), (0, 1), (1, 1), (1, 0), (2, 0)]逆順にたどる前、route配列にはゴールの位置が記録されています。ここからコストが一つずつ小さくなる方向に進みながらroute配列に座標を加えていきます。コストが０のところまで来たら終了です。
※チェックする座標の添字は、縦方向は0以上h未満、横方向は0以上w未満の範囲であることに注意しましょう。Pythonでは負の添字は配列の最後尾を参照してしまい、迷路が上下で繋がったような判定になる可能性があります。迷路サイズより大きい添字はエラーとなります。
route配列を逆順にひっくり返したら完成です。
大きな迷路で
#########################
# 迷路
#########################
maze = ['###########################################',
's-#---#-----------#-----------------------#',
'#-###-###########-#-#################-###-#',
'#---#-----------#-#-#---------------#-#-#-#',
'###-###########-#-#-#####-#####-###-###-#-#',
'#-#---------#-#-#-------#-#---#-#-#-----#-#',
'#-#######-###-#-#######-###-###-#-#####-#-#',
'#---------#-------#---------#-----#-----#-#',
'#####-###-#####-###-#####-###-#####-#####-#',
'#---#-#-#-#---#-#---#-#---#---#-----#-----#',
'#-#-#-#-#-###-#-#-###-###-#-###-###-#-###-#',
'#-#-#-#-#---#-#-#-#-----#-#-#---#-#-#-#-#-#',
'#-#-#-#-#####-#-#######-###-#-###-#-#-#-#-#',
'#-#-#-#-------#-------#-----#-#---#-#-#-#-#',
'#-#-#-#-#####-###-###-#######-###-###-#-#-#',
'#-#-#-#---#-#---#-#-#-----------#-----#-#-#',
'#-#-#-#####-###-###-###########-###-###-#-#',
'#-#-#---------#-------------#-#-#-#-#---#-#',
'#-#-#####-###-#-###-###-#####-#-#-#-###-#-#',
'#-#-----#-#-#-#-#-#---#-#-------#-#---#-#-#',
'#-#####-###-#-###-#####-###-###-#-###-#-#-#',
'#-----#-----#---------------#-#-#---#-#---#',
'###-#-#-###-###-#########-###-###-###-###-#',
'#-#-#-#-#-#-#---#-------#-#-------------#-#',
'#-###-###-###-#####-#-###-###-#######-###-#',
'#-------------#---#-#-#-----#-#---#---#---#',
'#-###-#######-###-###-#-#####-###-###-#-###',
'#-#-#-#-#-------#-----#-#-------#---#-#---#',
'#-#-#-#-###-###-#-#####-#####-#####-#-###-#',
'#-#-#-#-#---#-#-#-#---------#-------#---#-#',
'#-#-#-#-#-###-###-#-#-#######-#####-###-#-#',
'#-#-#---#-#-------#-#-#-------#---#-#---#-#',
'#-#-#####-#-#######-#-#########-###-#-###-#',
'#-#-------#---------#---------------#-#---g',
'###########################################']
計算オーダーは置いておきまして、よくできています。
