10/15(火)-10/19(土)　岐阜県（南濃温泉「水晶の湯」）で自動運転車の実証実験を行います☆彡

21-1. 数式を使わずにD-waveマシンの使い方を学ぶ

やること

量子コンピュータの使い方を検索すると、だいたい数式ばかり出てきて憤死します。Σ←これが出てくるとだいたいアウトです。今日は数式を使わずにD-waveの基本的な使い方を学んでみます。

目標は「n個の量子ビットの中からm個を１にする」ができるようになることです。たぶんこれができればＯＫなはず。

イジングとかハミルトニアンとかキューボとかそういった外国語は使いません（使えません）。

実行環境

D-wave leapに登録すると月に１分間だけ実機での計算時間がもらえます。API tokenが手に入るので、コード中の「#D-waveの設定」のところに記述します。

The Leap™ Quantum Cloud Service | D-Wave
D-Wave Leap quantum cloud service delivers immediate, real-time access to our Advantage quantum computers and quantum hybrid solver services.
www.dwavesys.com

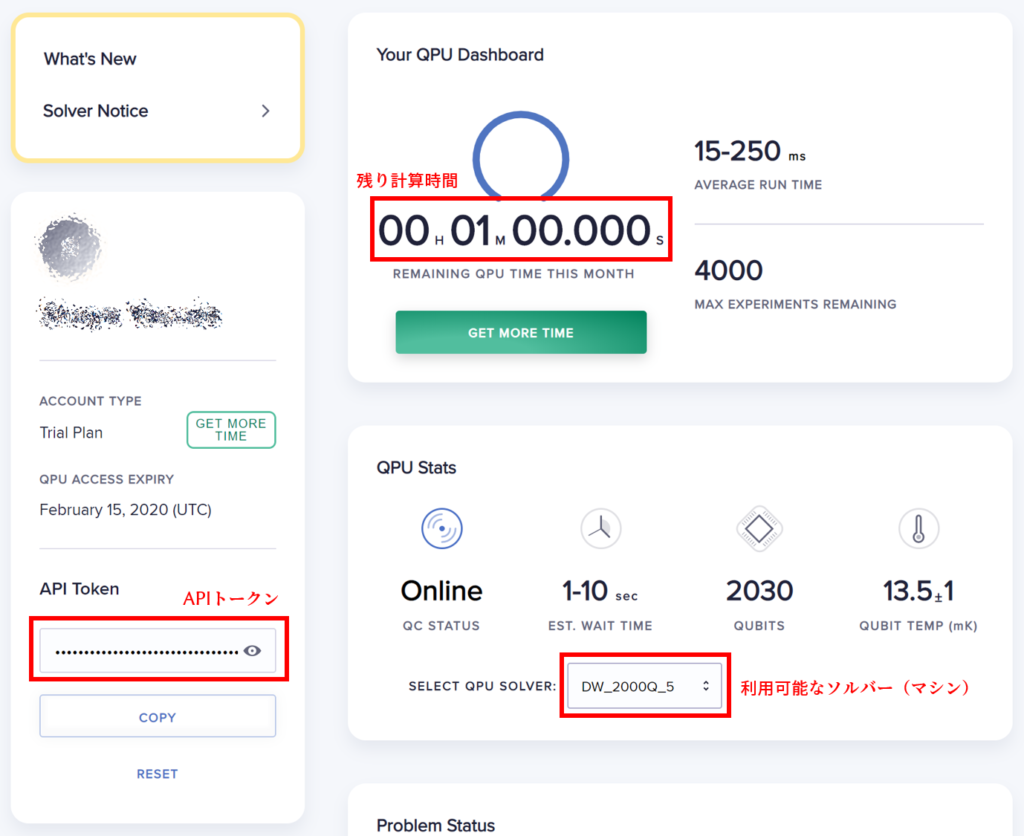
WinPython3.6をおすすめしています。

WinPython - Browse /WinPython_3.6/3.6.7.0 at SourceForge.net
Portable Scientific Python 2/3 32/64bit Distribution for Windows
sourceforge.net

pip

必要なパッケージをインストールしておきます。

pip install pyqubo
pip install dwave-ocean-sdk

４つの量子ビットの中から２つを１にする

能書きはさておき、答えです。ここでは「４つの量子ビットの中から２つを１にする」をしています。

from pyqubo import Binary
from dwave.system.composites import EmbeddingComposite
from dwave.system.samplers import DWaveSampler

#量子ビットを４つ用意する
q0, q1, q2, q3  = Binary('q0'), Binary('q1'), Binary('q2'), Binary('q3')

#条件を記述する
H = (q0 + q1 + q2 + q3 - 2)**2

#コンパイル
model = H.compile()
qubo, offset = model.to_qubo()
print('qubo\n{}'.format(qubo))

#D-waveの設定
sampler = EmbeddingComposite(DWaveSampler(endpoint='https://cloud.dwavesys.com/sapi',
                                          token='your_token', #あなたのAPIトークンを記入
                                          solver='DW_2000Q_5')) #利用可能なソルバーを指定

#サンプリングしまくる
response = sampler.sample_qubo(qubo, num_reads=1000)

#レスポンスの確認
print('response')
for (sample, energy, occurrence, _) in response.data():
    print('Sample:{} Energy:{} Occurrence:{}'.format(list(sample.values()), energy, occurrence))
qubo
{('q0', 'q1'): 2.0, ('q0', 'q2'): 2.0, ('q0', 'q3'): 2.0, ('q1', 'q2'): 2.0, ('q1', 'q3'): 2.0, ('q2', 'q3'): 2.0, ('q0', 'q0'): -3.0, ('q1', 'q1'): -3.0, ('q2', 'q2'): -3.0, ('q3', 'q3'): -3.0}
response
Sample:[1, 0, 1, 0] Energy:-4.0 Occurrence:133
Sample:[0, 1, 1, 0] Energy:-4.0 Occurrence:1
Sample:[0, 0, 1, 1] Energy:-4.0 Occurrence:1
Sample:[1, 1, 0, 0] Energy:-4.0 Occurrence:1
Sample:[0, 1, 0, 1] Energy:-4.0 Occurrence:147
Sample:[0, 1, 0, 1] Energy:-4.0 Occurrence:1
Sample:[1, 1, 0, 0] Energy:-4.0 Occurrence:178
Sample:[1, 0, 0, 1] Energy:-4.0 Occurrence:147
Sample:[0, 0, 1, 1] Energy:-4.0 Occurrence:157
Sample:[0, 1, 1, 0] Energy:-4.0 Occurrence:154
Sample:[0, 1, 1, 1] Energy:-3.0 Occurrence:1
Sample:[0, 1, 1, 1] Energy:-3.0 Occurrence:3
Sample:[1, 1, 0, 1] Energy:-3.0 Occurrence:1
Sample:[1, 1, 0, 1] Energy:-3.0 Occurrence:5
Sample:[1, 0, 0, 0] Energy:-3.0 Occurrence:12
Sample:[1, 1, 0, 1] Energy:-3.0 Occurrence:7
Sample:[1, 1, 0, 1] Energy:-3.0 Occurrence:1
Sample:[0, 1, 0, 0] Energy:-3.0 Occurrence:12
Sample:[1, 0, 1, 1] Energy:-3.0 Occurrence:6
Sample:[0, 0, 0, 1] Energy:-3.0 Occurrence:12
Sample:[0, 0, 1, 0] Energy:-3.0 Occurrence:5
Sample:[0, 1, 1, 1] Energy:-3.0 Occurrence:5
Sample:[1, 1, 1, 0] Energy:-3.0 Occurrence:10

Occurrence が高い解が６個あり、よく見ると「４個の量子ビットの中から２つを１にする」ができています。６個出てきたのは 4C2=6 であることからも納得できます。

同様に「４個の量子ビットの中から３つを１にする」を行うには

#条件を記述する
H = (q0 + q1 + q2 + q3 - 3)**2

に書き換えます。

qubo
{('q0', 'q1'): 2.0, ('q0', 'q2'): 2.0, ('q0', 'q3'): 2.0, ('q1', 'q2'): 2.0, ('q1', 'q3'): 2.0, ('q2', 'q3'): 2.0, ('q0', 'q0'): -5.0, ('q1', 'q1'): -5.0, ('q2', 'q2'): -5.0, ('q3', 'q3'): -5.0}
response
Sample:[1, 1, 0, 1] Energy:-9.0 Occurrence:227
Sample:[0, 1, 1, 1] Energy:-9.0 Occurrence:220
Sample:[1, 0, 1, 1] Energy:-9.0 Occurrence:233
Sample:[1, 1, 1, 0] Energy:-9.0 Occurrence:232
Sample:[1, 0, 1, 1] Energy:-9.0 Occurrence:4
Sample:[1, 0, 1, 1] Energy:-9.0 Occurrence:5
Sample:[1, 1, 1, 0] Energy:-9.0 Occurrence:2
Sample:[1, 1, 1, 0] Energy:-9.0 Occurrence:2
Sample:[0, 1, 0, 1] Energy:-8.0 Occurrence:17
Sample:[1, 0, 0, 1] Energy:-8.0 Occurrence:12
Sample:[1, 1, 0, 0] Energy:-8.0 Occurrence:4
Sample:[0, 0, 1, 1] Energy:-8.0 Occurrence:12
Sample:[0, 1, 1, 0] Energy:-8.0 Occurrence:8
Sample:[1, 0, 1, 0] Energy:-8.0 Occurrence:8
Sample:[1, 1, 1, 1] Energy:-8.0 Occurrence:14

４個出ました。4C3=4 ですから納得です。

だいたいパターンが分かってきました。

とにかく、解きたい問題を「n個の量子ビットの中からm個を１にする」に帰着できれば、D-waveが適用できるのかなと思います。

４つの量子ビットの中から１つまたは２つを１にする

「４つの量子ビットの中から１つまたは２つを１にする」にはどうしたらよいでしょうか。

#条件を記述する
H = (q0 + q1 + q2 + q3 - 1.5)**2

１と２の中間ということで1.5を引いてみます。こうすると、q0 + q1 + q2 + q3 が１であっても２であっても、どちらも H=0.25（最小値）となります。

qubo
{('q0', 'q1'): 2.0, ('q0', 'q2'): 2.0, ('q0', 'q3'): 2.0, ('q1', 'q2'): 2.0, ('q1', 'q3'): 2.0, ('q2', 'q3'): 2.0, ('q0', 'q0'): -2.0, ('q1', 'q1'): -2.0, ('q2', 'q2'): -2.0, ('q3', 'q3'): -2.0}
response
Sample:[0, 0, 1, 0] Energy:-2.0 Occurrence:109
Sample:[0, 1, 0, 0] Energy:-2.0 Occurrence:98
Sample:[0, 1, 1, 0] Energy:-2.0 Occurrence:80
Sample:[1, 0, 0, 0] Energy:-2.0 Occurrence:97
Sample:[1, 0, 1, 0] Energy:-2.0 Occurrence:103
Sample:[1, 1, 0, 0] Energy:-2.0 Occurrence:89
Sample:[0, 0, 0, 1] Energy:-2.0 Occurrence:105
Sample:[0, 0, 1, 1] Energy:-2.0 Occurrence:96
Sample:[0, 1, 0, 1] Energy:-2.0 Occurrence:108
Sample:[1, 0, 0, 1] Energy:-2.0 Occurrence:90
Sample:[1, 0, 1, 0] Energy:-2.0 Occurrence:5
Sample:[0, 0, 1, 1] Energy:-2.0 Occurrence:2
Sample:[1, 1, 0, 0] Energy:-2.0 Occurrence:6
Sample:[0, 1, 0, 1] Energy:-2.0 Occurrence:10
Sample:[1, 0, 0, 1] Energy:-2.0 Occurrence:1
Sample:[1, 1, 0, 1] Energy:0.0 Occurrence:1

実行結果を見ると、4C1 + 4C2 = 10パターンが見つかっています。

どうしてsamplingと呼ぶの？

量子アニーリングって、ほぼ絶対零度の状態からわずかに温度を上げてゆっくり冷やすから「アニーリング」なのですが、では最適化のコマンドが「anneal」ではなく「sample」なのはなぜでしょうか。MDR社の湊社長に伺ったところ、

“理想的な”量子コンピュータが存在すれば、１回のアニーリングで最適解が求まる。

しかし、実際には次の理由によりノイズが加わり、不確実となる。

  • アニーリング時間が無限ではなく有限
  • 電磁波や振動の影響を受ける

そこで、不確実なアニーリングを繰り返し行い、統計的に「まあこれが最適解やろ」な解を探す作業を行う。何回か取り出して元の姿を推測するから「サンプリング」と呼ぶ。

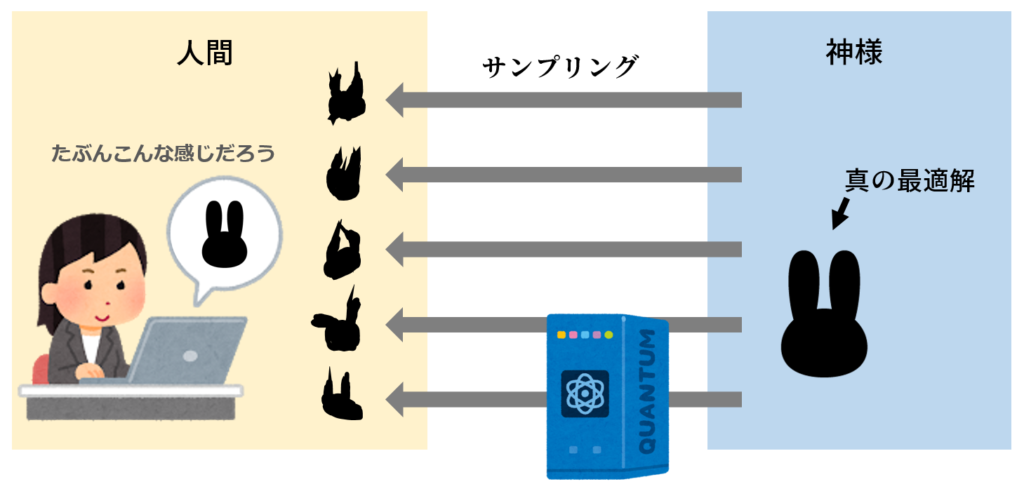
まとめ

あちこち文献を見ましたが、数式を使わずに説明するという無謀なことをやっている方はいるのでしょうか。これで最低限のＤ-waveの使い方が分かりました。

次の記事では、いよいよD-waveでパズルを解いてみます。

21-2. 量子アニーリング（D-wave）でテント・アンド・ツリーパズルを解く（初めて編）
やること20-2では、GAでテント・アンド・ツリーというパズルを解きました。パズルのルールについては記事をご参照ください。このパズルは量子コンピュータとも相性が良さそうな...
vigne-cla.com
2019/10/28
タイトルとURLをコピーしました