やること
20-2では、GAでテント・アンド・ツリーというパズルを解きました。パズルのルールについては記事をご参照ください。
このパズルは量子コンピュータとも相性が良さそうなので、D-waveマシンで解いてみます。
実行環境
WinPython3.6をおすすめしています。
D-waveの使い方についてはこちらをご参照ください。
考え方1
テントが入る可能性があるマス(つまり木の4近傍のマス)の数だけ量子ビットを用意し、0であれば芝生、1であればテントとします。
例題1の場合は13ヶ所です。

GAで解いた際のペナルティは次のようなもので、このペナルティが0に近づくように最適化しました。
- 木の4近傍にあるテントの数が1または2でなければペナルティ
- テントの8近傍にある他のテントの数が0でなければペナルティ
- 各行、各列の「テントの数」と「数字」の差がペナルティ
D-waveでは、すべての条件を「n個の中からm個を1にする」で表現することを目指します。
考え方2
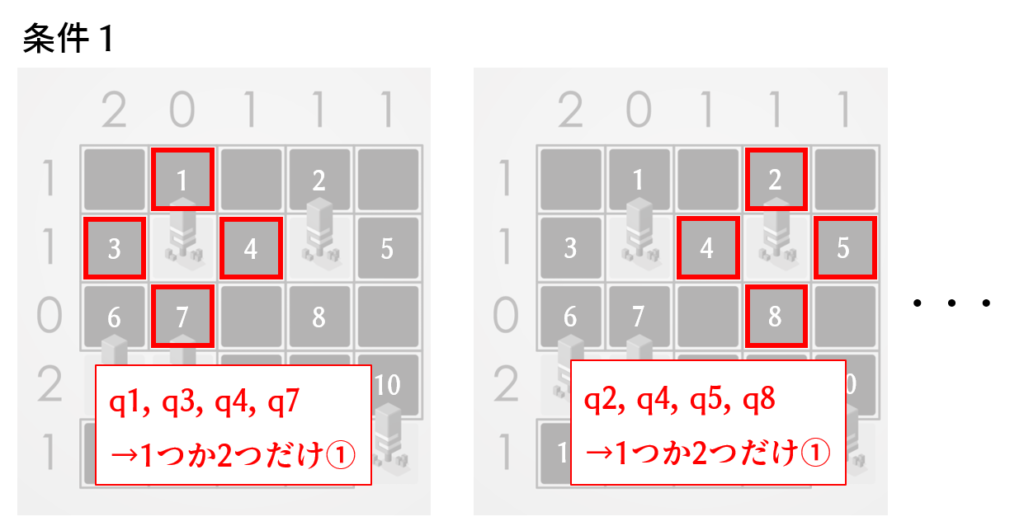
条件1「木の4近傍にあるテントの数が1または2でなければならない」
各木の4近傍のマスについて、1つか2つだけ1になるように設定すればよさそうです。「q1とq3が両方とも1になっていいの?」という疑問は湧きますが、これは条件2で阻止します。この条件設定は木の数だけあります。
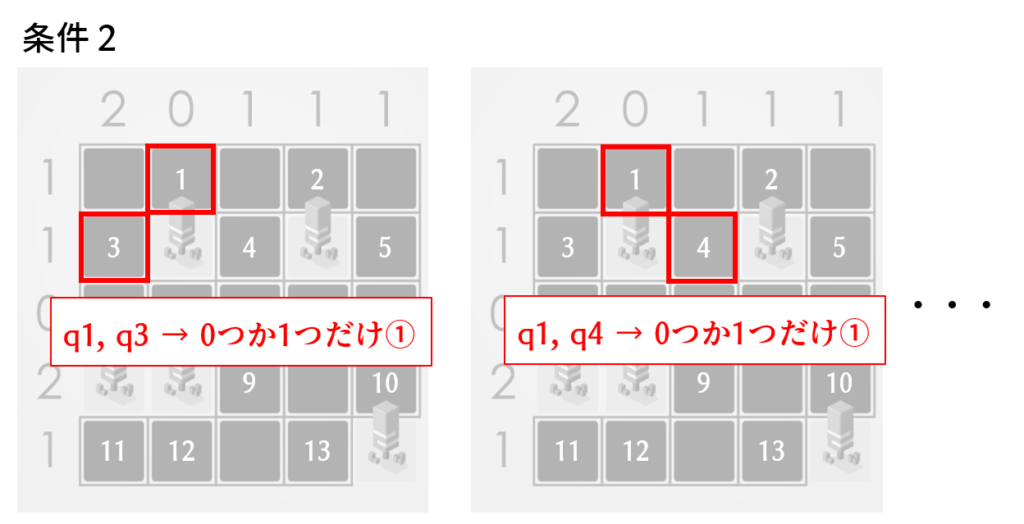
条件2「テントの8近傍にある他のテントの数が0でなければならない」
8近傍で隣接する2つのマスのうち、0つまたは1つだけ1になるように設定すればよさそうです(0つとは)。両方とも1であってはならないということです。この条件設定はいくつあるのでしょうか、数えるのが面倒くさそうです。
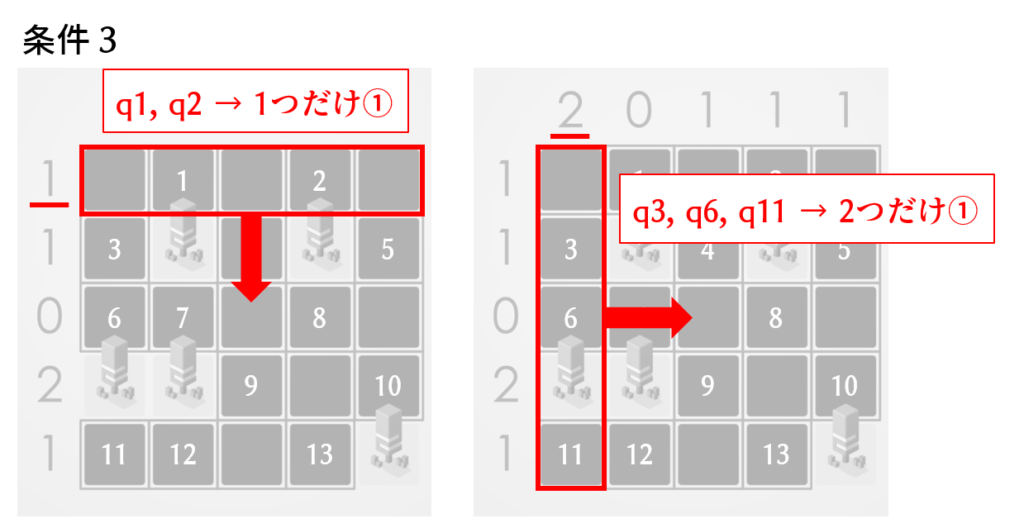
条件3「各行、各列の “テントの数” と “数字” が一致する」
これが一番分かりやすいかもしれません。「n個の中からm個を1にする」がシンプルに適用できます。ここは合計10個の条件設定になります。
import
必要なパッケージをimportします。いよいよ使うぞ、D-wave!(気合)
import numpy as np
from scipy import signal
from dwave.system.composites import EmbeddingComposite
from dwave.system.samplers import DWaveSampler
from pyqubo import Binaryパズル問題
パズル問題は ‘-‘ と ‘t’ で表現します。horizontal は右方向に並んだ数字、vertical は縦方向に並んだ数字です。
#============================
# パズル
#============================
pazzle = ['-----',
'-t-t-',
'-----',
'tt---',
'----t']
horizontal = [2,0,1,1,1]
vertical = [1,1,0,2,1]前処理を行います。
#============================
# パズルの変換
#============================
tree = []
for line in pazzle:
line = line.replace('-', '0')
line = line.replace('t', '1')
tree.append(list(line))
tree = np.array(tree, dtype=int)
print('tree\n{}'.format(tree))
tent = np.zeros(tree.shape, dtype=int)
print('tent\n{}'.format(tent))
horizontal = np.array(horizontal)
print('horizontal\n{}'.format(horizontal))
vertical = np.array(vertical)
print('vertical\n{}'.format(vertical))tree
[[0 0 0 0 0]
[0 1 0 1 0]
[0 0 0 0 0]
[1 1 0 0 0]
[0 0 0 0 1]]
tent
[[0 0 0 0 0]
[0 0 0 0 0]
[0 0 0 0 0]
[0 0 0 0 0]
[0 0 0 0 0]]
horizontal
[2 0 1 1 1]
vertical
[1 1 0 2 1]木の配列、テントの配列(空っぽ)ができました。
量子ビットの用意と条件の記述
初心者ですから、ひとつひとつ地道に書いていきます。
#============================
# 量子ビットの用意
#============================
q01, q02, q03 = Binary('q01'), Binary('q02'), Binary('q03')
q04, q05, q06 = Binary('q04'), Binary('q05'), Binary('q06')
q07, q08, q09 = Binary('q07'), Binary('q08'), Binary('q09')
q10, q11, q12, q13 = Binary('q10'), Binary('q11'), Binary('q12'), Binary('q13')
#============================
# 条件の記述
#============================
#条件1、各木の4近傍のマスについて、1つか2つだけ1になる
H = (q01 + q03 + q04 + q07 - 1.5)**2
H += (q02 + q04 + q05 + q08 - 1.5)**2
H += (q06 + q11 - 1.5)**2
H += (q07 + q09 + q12 - 1.5)**2
H += (q10 + q13 - 1.5)**2
#条件2、8近傍で隣接する2つのマスのうち、0つまたは1つだけ1になる(多すぎる!(怒))
H += (q01 + q03 - 0.5)**2
H += (q01 + q04 - 0.5)**2
H += (q02 + q04 - 0.5)**2
H += (q02 + q05 - 0.5)**2
H += (q03 + q06 - 0.5)**2
H += (q03 + q07 - 0.5)**2
H += (q04 + q07 - 0.5)**2
H += (q04 + q08 - 0.5)**2
H += (q05 + q08 - 0.5)**2
H += (q06 + q07 - 0.5)**2
H += (q07 + q09 - 0.5)**2
H += (q08 + q09 - 0.5)**2
H += (q08 + q10 - 0.5)**2
H += (q09 + q12 - 0.5)**2
H += (q09 + q13 - 0.5)**2
H += (q10 + q13 - 0.5)**2
H += (q11 + q12 - 0.5)**2
#条件3、各行、各列の "テントの数" と "数字" が一致する
#vertical
H += (q01 + q02 - 1)**2
H += (q03 + q04 + q05 - 1)**2
H += (q06 + q07 + q08 - 0)**2
H += (q09 + q10 - 2)**2
H += (q11 + q12 + q13 - 1)**2
#horizontal
H += (q03 + q06 + q11 - 2)**2
H += (q01 + q07 + q12 - 0)**2
H += (q04 + q09 - 1)**2
H += (q02 + q08 + q13 - 1)**2
H += (q05 + q10 - 1)**2うーん、これfor文で設定できそうですが、それはそれで正しい道なのでしょうか。
サンプリングの実行
21-1と同様に実行します。結果は response に格納されるのですが、なんともよく分からないオブジェクトですので、順番に開いて確認しながら、「もっとも多く観測した状態」を best_sample に保存します。
#コンパイル
model = H.compile()
qubo, offset = model.to_qubo()
print('qubo\n{}'.format(qubo))
#D-waveの設定
sampler = EmbeddingComposite(DWaveSampler(endpoint='https://cloud.dwavesys.com/sapi',
token='your_token',
solver='DW_2000Q_5'))
#サンプリングしまくる
response = sampler.sample_qubo(qubo, num_reads=1000)
#レスポンスの確認
best_occurrence = 0
print('response')
for (sample, energy, occurrences, _) in response.data():
print('Sample:{} Energy:{} Occurrences:{}'.format(list(sample.values()), energy, occurrences))
#最頻解であれば保存しておく
if occurrences > best_occurrence:
best_occurrence = occurrences
best_sample = np.array(list(sample.values()))
#最頻解の確認
print('best_sample\n{}'.format(best_sample))qubo
{('q01', 'q03'): 4.0, ('q01', 'q04'): 4.0, ('q01', 'q07'): 4.0, ('q01', 'q02'): 2.0, ('q01', 'q12'): 2.0, ('q03', 'q04'): 4.0, ('q03', 'q07'): 4.0, ('q03', 'q06'): 4.0, ('q03', 'q05'): 2.0, ('q03', 'q11'): 2.0, ('q04', 'q07'): 4.0, ('q02', 'q04'): 4.0, ('q04', 'q05'): 4.0, ('q04', 'q08'): 4.0, ('q04', 'q09'): 2.0, ('q07', 'q09'): 4.0, ('q07', 'q12'): 4.0, ('q06', 'q07'): 4.0, ('q07', 'q08'): 2.0, ('q02', 'q05'): 4.0, ('q02', 'q08'): 4.0, ('q02', 'q13'): 2.0, ('q05', 'q08'): 4.0, ('q05', 'q10'): 2.0, ('q08', 'q09'): 2.0, ('q08', 'q10'): 2.0, ('q06', 'q08'): 2.0, ('q08', 'q13'): 2.0, ('q06', 'q11'): 4.0, ('q11', 'q12'): 4.0, ('q11', 'q13'): 2.0, ('q09', 'q12'): 4.0, ('q09', 'q13'): 2.0, ('q09', 'q10'): 2.0, ('q12', 'q13'): 2.0, ('q10', 'q13'): 4.0, ('q01', 'q01'): -2.0, ('q03', 'q03'): -6.0, ('q04', 'q04'): -6.0, ('q07', 'q07'): -2.0, ('q02', 'q02'): -4.0, ('q05', 'q05'): -4.0, ('q08', 'q08'): -2.0, ('q06', 'q06'): -4.0, ('q11', 'q11'): -6.0, ('q09', 'q09'): -6.0, ('q12', 'q12'): -2.0, ('q10', 'q10'): -6.0, ('q13', 'q13'): -4.0}
response
Sample:[0, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0] Energy:-24.0 Occurrences:600
Sample:[0, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0] Energy:-24.0 Occurrences:103
Sample:[0, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0] Energy:-24.0 Occurrences:22
Sample:[0, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0] Energy:-24.0 Occurrences:8
Sample:[0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0] Energy:-20.0 Occurrences:23
Sample:[0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0] Energy:-20.0 Occurrences:3
Sample:[0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0] Energy:-20.0 Occurrences:3
Sample:[0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0] Energy:-20.0 Occurrences:3
Sample:[0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0] Energy:-20.0 Occurrences:1
Sample:[0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0] Energy:-20.0 Occurrences:1
Sample:[0, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0] Energy:-18.0 Occurrences:2
Sample:[0, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0] Energy:-18.0 Occurrences:1
Sample:[0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0] Energy:-16.0 Occurrences:2
Sample:[0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0] Energy:-16.0 Occurrences:17
Sample:[0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0] Energy:-16.0 Occurrences:6
Sample:[0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0] Energy:-16.0 Occurrences:39
Sample:[0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0] Energy:-16.0 Occurrences:163
Sample:[0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0] Energy:-16.0 Occurrences:2
Sample:[0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0] Energy:-16.0 Occurrences:1
best_sample
[0 1 1 0 0 0 0 0 1 1 1 0 0]もっとも多く観測した量子ビットの状態は [0 1 1 0 0 0 0 0 1 1 1 0 0] でした。というかよく見たら同じ解がいっぱいありますね。
結果の確認
結果をtent配列に戻してやります。
#============================
# テントの位置を確認
#============================
#畳み込み用のフィルタ
filter_4 = np.array([[0, 1, 0],
[1, 0, 1],
[0, 1, 0]], dtype=int)
#木の4近傍のマスをあぶり出す
mask_candidate = (signal.convolve2d(tree, filter_4, mode='same') > 0) * (tree == 0)
print('mask_candidate\n{}'.format(mask_candidate))
#そこに結果を入れる
tent[mask_candidate] = best_sample
print('tent\n{}'.format(tent))mask_candidate
[[False True False True False]
[ True False True False True]
[ True True False True False]
[False False True False True]
[ True True False True False]]
tent
[[0 0 0 1 0]
[1 0 0 0 0]
[0 0 0 0 0]
[0 0 1 0 1]
[1 0 0 0 0]]一致したでしょうか?

まとめ
以上、「初めてD-waveを使ってみた」でした。10*10サイズの問題にも挑戦したかったですが、条件をすべて手で記述するのは大変そうなので、今回はここまでとします。もっと賢い方法を知っている方は教えてください。



