やること
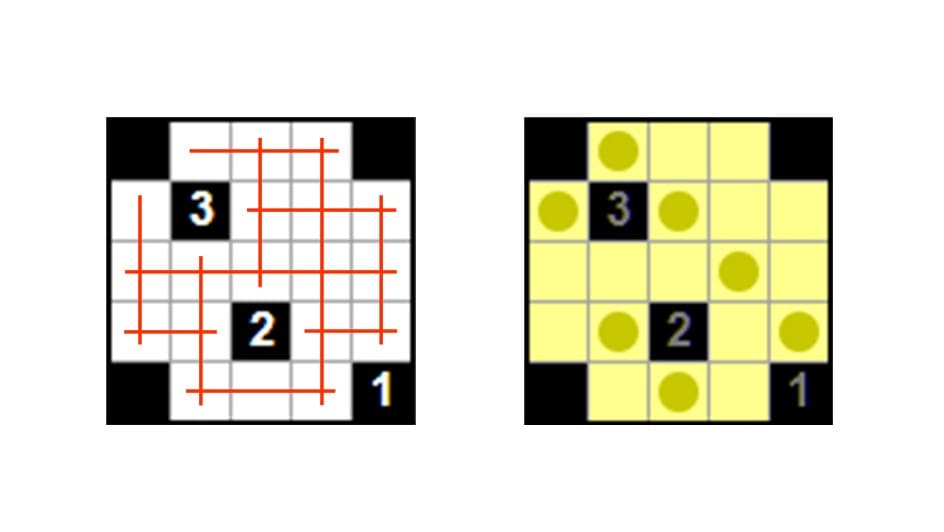
どんどん行きます。QUBOで美術館(ライトアップ)を解いてみましょう。
最小問題を用意しました。(※サムネイルとは違う問題です)

答えがこちらです。
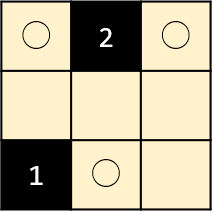
ライトを置くと上下左右にビーム状に光が届きます。ライトの光は他のライトに当たってはいけません。数字マスはその4近傍のライトの個数を指定しています。部屋全体を明るくするにはどこにライトを置けば良いか?というパズルです。
おさらい
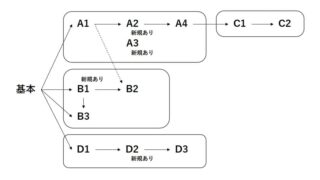
今回は基本と応用A1の条件設定を使います。
基本「n個の量子ビットからm個を1にする」
応用A1「n個の量子ビットからm個またはm+1個を1にする」
その他の設定可能な条件式も気になる方は過去のまとめ記事をご参照ください。
どうやって美術館を解くのか
まず、白マスを量子ビットに対応させ、結果が1ならライトを置くことにします。

赤線に着目すると、各ラインには0個または1個のライトを置く必要があります。1個置くのは分かりますが、実は0個の可能性もあります。すべて脇から照らしてくれればOKですから。ライン上に2個以上置いてしまうと「ライトの光は他のライトに当たってはいけない」に反します。応用A1の条件設定を使って赤線の数だけ設定します。
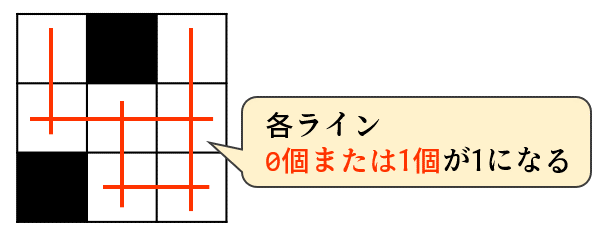
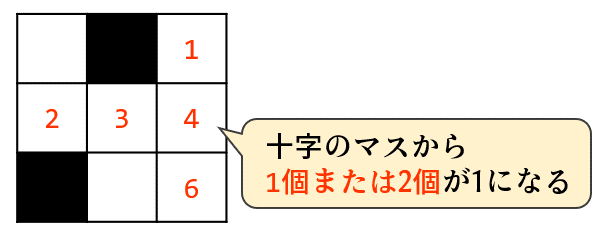
次に、一つの白マスに着目して、十字関係のマス(ライトが置かれる可能性があるマス)には1個または2個のライトがある必要があります。少なくとも1個はないとこのマスが照らされませんし、よく考えると1個だけとは限らず、2個の可能性もあります(光がクロスするのはOKなので)。3個以上はあり得ません。ということでこちらも応用A1を使って各白マスに設定します。
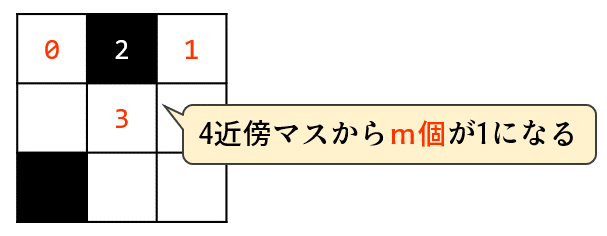
最後に、数字マスに着目して「4近傍からm個だけ1になる」を設定します。これはシンプルですね。
コード
条件設定の部分をよく確認してください。
from pyqubo import Binary
from dwave_qbsolv import QBSolv
#量子ビットを用意する
q0 = Binary('q0')
q1 = Binary('q1')
q2 = Binary('q2')
q3 = Binary('q3')
q4 = Binary('q4')
q5 = Binary('q5')
q6 = Binary('q6')
#横方向の各ライン、「0個または1個が1になる」=「0.5個が1になる」
H = 0
H += (q2 + q3 + q4 - 0.5)**2
H += (q5 + q6 - 0.5)**2
#縦方向の各ライン、同様
H += (q0 + q2 - 0.5)**2
H += (q3 + q5 - 0.5)**2
H += (q1 + q4 + q6 - 0.5)**2
#各白マスの十字関係、「1個または2個が1になる」=「1.5個が1になる」
H += (q0 + q2 - 1.5)**2
H += (q1 + q4 + q6 - 1.5)**2
H += (q0 + q2 + q3 + q4 - 1.5)**2
H += (q2 + q3 + q4 + q5 - 1.5)**2
H += (q2 + q3 + q1 + q6 - 1.5)**2
H += (q3 + q5 + q6 - 1.5)**2
H += (q4 + q5 + q6 - 1.5)**2
#各数字マス
H += (q0 + q1 + q3 - 2)**2
H += (q2 + q5 - 1)**2
#コンパイル
model = H.compile()
qubo, offset = model.to_qubo()
#分割サンプリング
response = QBSolv().sample_qubo(qubo, num_repeats=500)
#レスポンスの確認
print('response')
for (sample, energy, occurrence) in response.data():
print(f'Sample:{list(sample.values())} Energy:{energy} Occurrence:{occurrence}')Sample:[1, 1, 0, 0, 0, 1, 0] Energy:-19.0 Occurrence:421
Sample:[1, 0, 0, 1, 0, 0, 1] Energy:-18.0 Occurrence:81最適解を白マスに戻してやると、模範解答の通りになりました。

さいごに
今回は最小問題を試したのでちょっとショボい感じがしますが、大きな問題もこの方法で解けると思います。