やること
QUBOでペンシルパズルを解くのにもそろそろ飽きてきました。今後は、発展的な内容であれば解説はそこそこにして解く様子を見ていただきましょう。
今回は天体ショーパズル(Galaxies)を解きます。指定された点を中心に、点対称に領域を区切るパズルです。「飛び地」は禁止です。
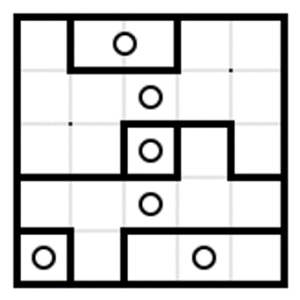
答えはこちらです。
おさらい
ナンプレ(数独)の解き方を予習してください。
QUBOで設定できる条件式については過去のまとめ記事をご参照ください↓
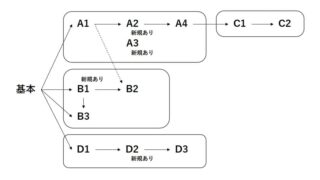
この問題では
- One-hot表現
- 基本「n個の量子ビットからm個を1にする」
- A3「2個の量子ビットが同時に1になったら報酬を与える」
- B1「2個の量子ビットを揃える」
を使用します。応用レベルですね。
どうやって天体ショーを解くのか?
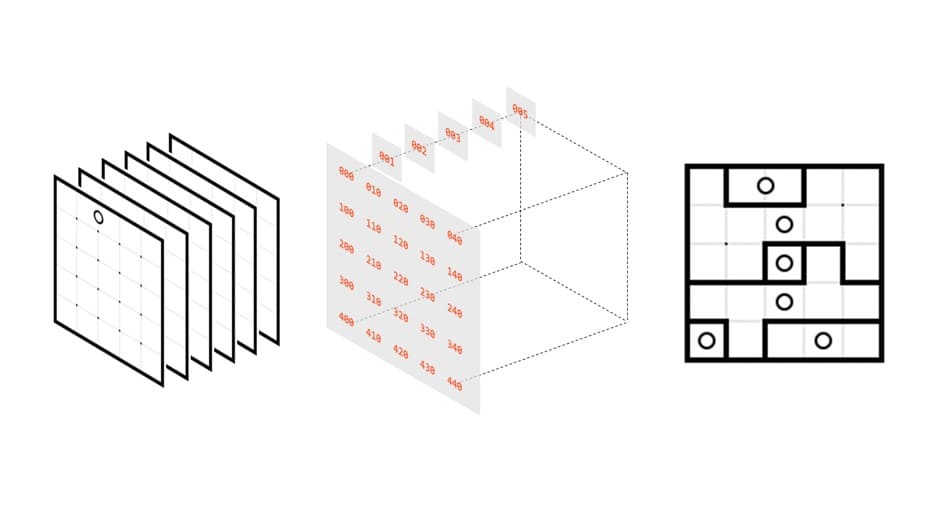
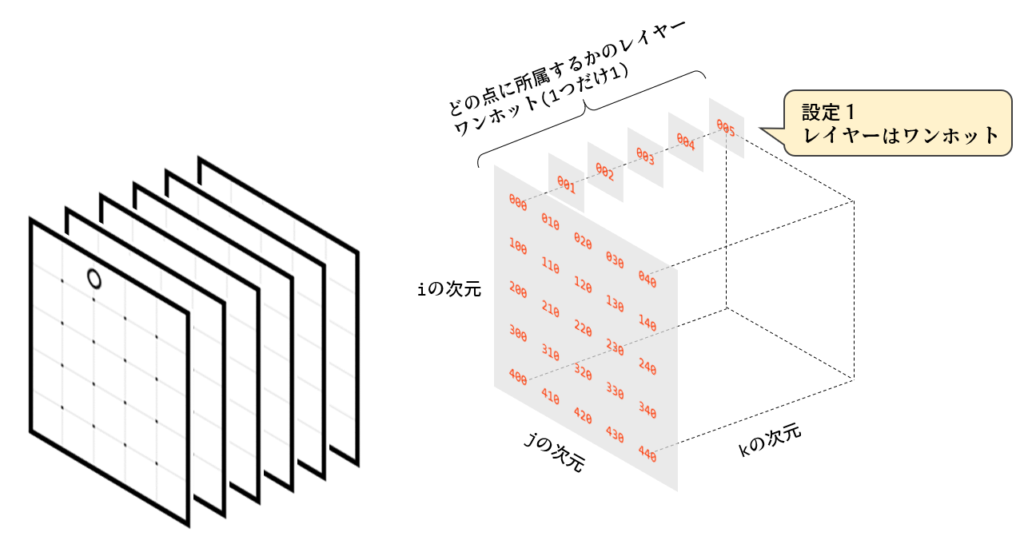
ナンプレのときと同じようにワンホット表現をするので5×5×6=150個の量子ビットを用意します。6はレイヤーの数で、与えられた6つの点を各レイヤーに振り分けて担当してもらいます。例えば、q001は1行目1列目の1番レイヤー(2個目の点が属するレイヤー)です。各レイヤーにおいて、結果が1であればその点の口分田となります。
まず設定1として、口分田は一つのレイヤーにしか属せないため、レイヤー方向にワンホットの設定をします。
次に、一つ一つのレイヤーに着目します。設定2として、点のマスは必ず1になるように設定します。点がマスに半分またがっているときは2マスとも1にします。
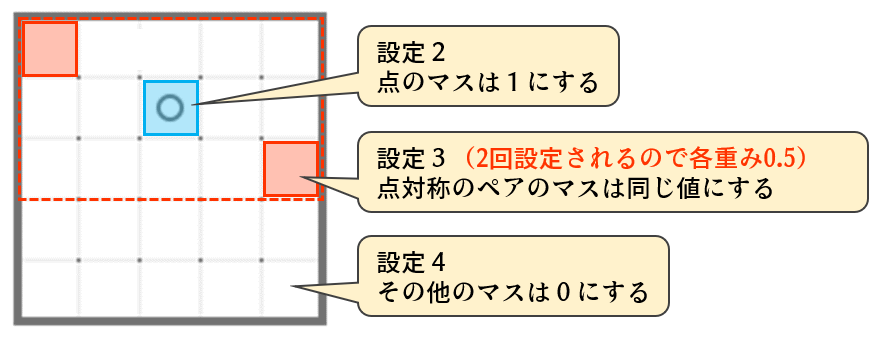
設定3として、点対称の関係にあるマスのペアは0、1の値が揃うようにします。設定4として、点対称になり得ない無関係なマスは必ず0にします。
ここまでの設定はすべて満たすことができるため重みに差をつけず、すべての重みを1にしています。注意点として、設定3はコードの都合上2回設定が実行されるので合計で重み1になるように各回は重み0.5としています。もし重複実行しないようにコードを修正するのであれば重み1でOKです。
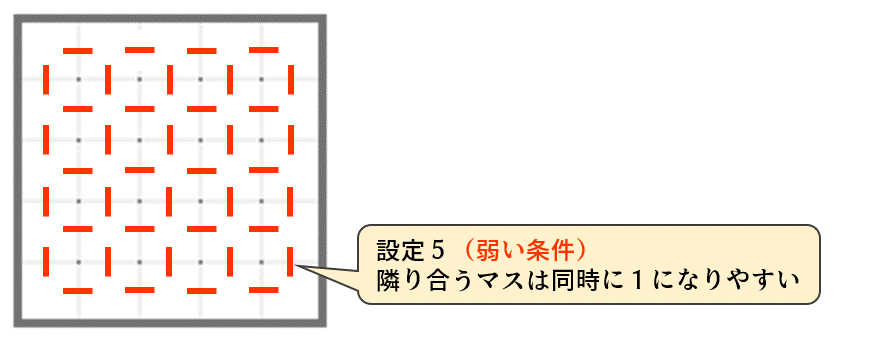
さて、このままでは飛び地ができる可能性があるため、隣り合うマスは同時に1になりやすいという弱い設定を加えます(設定5)。この条件は叶わない場所が必ずあるので、重みはオーダーを落として0.1とします。
コード
まずは設定5なしで実行してみます。
import numpy as np
from pyqubo import Binary
from dwave_qbsolv import QBSolv
#パラメータ
h = 5
w = 5
dot_num = 6
dots = [(0, 1.5), (1, 2), (2, 2), (3, 2), (4, 0), (4, 3)]
#量子ビットを用意する
for i in range(h):
for j in range(w):
for k in range(dot_num):
command = f'q{i}{j}{k} = Binary(\'q{i}{j}{k}\')'
print(command)
exec(command)
#各マスは一つのレイヤーに所属する(=kの次元がワンホット)
H = 0
for i in range(h):
for j in range(w):
command = f'H += (q{i}{j}0 + q{i}{j}1 + q{i}{j}2 + q{i}{j}3 + q{i}{j}4 + q{i}{j}5 - 1)**2'
print(command)
exec(command)
#各レイヤー繰り返し
for n in range(dot_num):
#点の座標
d = dots[n]
#各マスをチェックして
for i in range(h):
for j in range(w):
target = (int(d[0] + (d[0] - i)), int(d[1] + (d[1] - j)))
#点と一致していればそのマスは「1にする」(半分重なりに注意)
if -0.5 <= (i - d[0]) <= 0.5 and -0.5 <= (j - d[1]) <= 0.5:
command = f'H += (q{i}{j}{n} - 1)**2'
print(command)
exec(command)
#点を挟んで対称のマスが存在すればその2マスは「2個の量子ビットを揃える」
elif 0 <= target[0] < h and 0 <= target[1] < w:
"""
ここ注意、2回設定されるので重みは各0.5にすること
"""
command = f'H += 0.5 * (q{i}{j}{n} - q{target[0]}{target[1]}{n})**2'
print(command)
exec(command)
else:
#相手がいなければそのマスは無関係なので「0にする」
command = f'H += (q{i}{j}{n} - 0)**2'
print(command)
exec(command)
#コンパイル
model = H.compile()
qubo, offset = model.to_qubo()
#分割サンプリング
response = QBSolv().sample_qubo(qubo, num_repeats=500)
#レスポンスの確認
print('response')
for (sample, energy, occurrence) in response.data():
print(f'Sample:{list(sample.values())} Energy:{energy} Occurrence:{occurrence}')
#レイヤー番号に戻して確認
box = np.array(list(sample.values())).reshape(h, w, dot_num)
ans = np.zeros((h, w), int)
for i in range(h):
for j in range(w):
ans[i, j] = np.argmax(box[i, j, :])
print(ans)response
Sample:[0, 1, 0,...,0, 0, 1] Energy:-32.0 Occurrence:7
[[1 0 0 2 1]
[1 1 1 1 1]
[1 2 2 2 1]
[3 3 3 3 3]
[4 2 5 5 5]]
Sample:[0, 1, 0,...,0, 0, 1] Energy:-32.0 Occurrence:89
[[1 0 0 1 1]
[1 1 1 1 1]
[1 1 2 3 1]
[3 3 3 3 3]
[4 3 5 5 5]]
Sample:[0, 1, 0,...,0, 0, 1] Energy:-32.0 Occurrence:3
[[1 0 0 1 1]
[2 2 1 2 2]
[1 1 2 3 1]
[2 2 3 2 2]
[4 3 5 5 5]]分かりますでしょうか。「飛び地あり」ですべての条件を満たした解がたくさん得られました。
さて、ここに設定5を追加します。重みは0.1であることに注意してください。
#隣り合うマスは同時に1になりやすい(一塊のブロックにするため)
for k in range(dot_num):
for i in range(h - 1):
for j in range(w):
command = f'H += -0.1 * (q{i}{j}{k} * q{i+1}{j}{k})'
print(command)
exec(command)
for j in range(w - 1):
for i in range(h):
command = f'H += -0.1 * (q{i}{j}{k} * q{i}{j+1}{k})'
print(command)
exec(command)response
Sample:[0, 1, 0,...,0, 0, 1] Energy:-34.10000000000001 Occurrence:234
[[1 0 0 1 1]
[1 1 1 1 1]
[1 1 2 3 1]
[3 3 3 3 3]
[4 3 5 5 5]]飛び地がなくなり、最適解が一つに絞られました。模範解答と一致しています。

【補足】設定5が完全に信頼できるものかどうか微妙です。今度ゆっくり考えます。。
さいごに
有名なペンシルパズルからローラーしているのですが、「スリザーリンク」や「ごきげんななめ」のような線で囲む系(または囲んではいけない系)の設定が難しくてできていません。コーヒー飲んで知能MAXで挑みましょう。