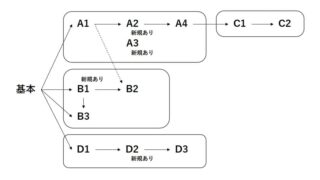
やること
完全に飽きましたが、まだ学べることがあるので引き続きQUBOでペンシルパズルを解いていきます。今回はドミノサパズル(Dominosa)を解いてみましょう。
このような問題です。
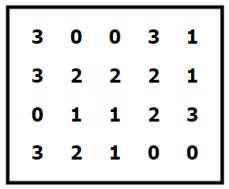
答えはこちらです。
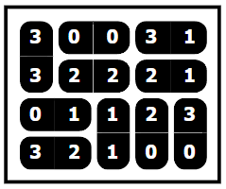
数字の上にドミノを置いていくパズルです。ドミノは0-0、0-1、0-2、・・・3-3まで重複なく10個用意されており、それらがピッタリ置けるように盤面は20個の数字からなります。「0-0が2箇所あるじゃん。どっちに0-0ドミノを使おうかな?」ということを考えるゲームです。
ちなみに数字の「4」が追加されるとドミノは15個、盤面には30個の数字が並びます。
おさらい
今回は基本の「n個の量子ビットからm個を1にする」だけを使用します。
その他のQUBOで設定できる条件式については過去のまとめ記事をご参照ください↓
どうやってドミノサを解くのか?
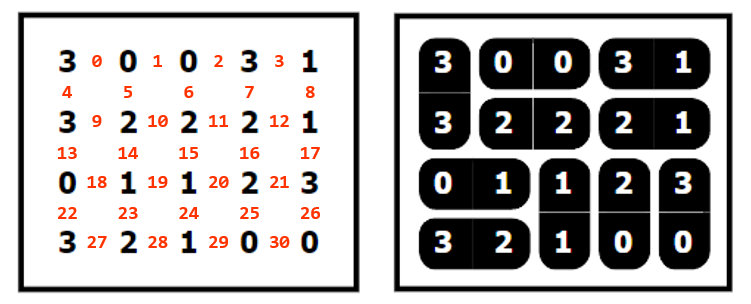
このパズルでは数字の接続箇所に量子ビットを割り当てると良いでしょう。全部で31量子ビットです。結果が1であればそこにドミノが置かれることになります。
まず設定1として、「各ドミノを1回だけ使用する」を考えます。例えば0-0のドミノが置ける場所は q1 と q30 の2箇所あります。これらのどちらか1箇所に置く必要があるので、「2個の量子ビットから1個を1にする」とします。ドミノは10種あるので10式になります。
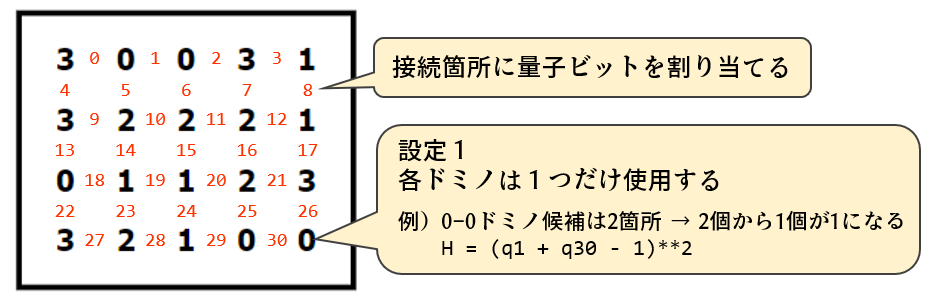
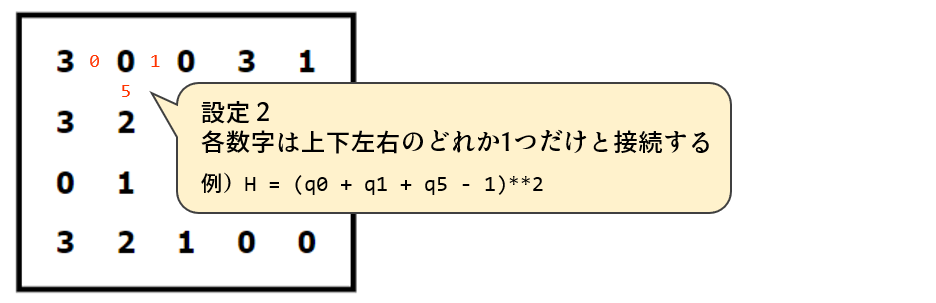
次に、各数字に着目します。設定2として、「各数字は上下左右のいずれかだけと接続される」とします。図の例では、この0は左・右・下のどれかとセットになるため、「3個の量子ビットから1個を1にする」とします。
コード
量子ビットの定義だけfor文を使っています(サボり)。
import numpy as np
from pyqubo import Binary
from dwave_qbsolv import QBSolv
#量子ビットを用意する
for i in range(31):
command = f'q{i:02} = Binary(\'q{i:02}\')'
print(command)
exec(command)
#各ドミノは1つだけ使用する
# 0-0
H = 0
H += (q01 + q30 - 1)**2
# 0-1
H += (q18 + q29 - 1)**2
# 0-2
H += (q05 + q06 + q25 - 1)**2
# 0-3
H += (q00 + q02 + q13 + q22 + q26 - 1)**2
# 1-1
H += (q08 + q19 + q24 - 1)**2
# 1-2
H += (q12 + q14 + q15 + q20 + q23 + q28 - 1)**2
# 1-3
H += (q03 + q17 - 1)**2
# 2-2
H += (q10 + q11 + q16 - 1)**2
# 2-3
H += (q07 + q09 + q21 + q27 - 1)**2
# 3-3
H += (q04 - 1)**2
#各数字は上下左右のどれか1つと接続する
H += ( q00 + q04 - 1)**2
H += (q00 + q01 + q05 - 1)**2
H += (q01 + q02 + q06 - 1)**2
H += (q02 + q03 + q07 - 1)**2
H += (q03 + q08 - 1)**2
H += (q04 + q09 + q13 - 1)**2
H += (q05 + q09 + q10 + q14 - 1)**2
H += (q06 + q10 + q11 + q15 - 1)**2
H += (q07 + q11 + q12 + q16 - 1)**2
H += (q08 + q12 + q17 - 1)**2
H += (q13 + q18 + q22 - 1)**2
H += (q14 + q18 + q19 + q23 - 1)**2
H += (q15 + q19 + q20 + q24 - 1)**2
H += (q16 + q20 + q21 + q25 - 1)**2
H += (q17 + q21 + q26 - 1)**2
H += (q22 + q27 - 1)**2
H += (q23 + q27 + q28 - 1)**2
H += (q24 + q28 + q29 - 1)**2
H += (q25 + q29 + q30 - 1)**2
H += (q26 + q30 - 1)**2
#コンパイル
model = H.compile()
qubo, offset = model.to_qubo()
print(f'offset\n{offset}')
#分割サンプリング
response = QBSolv().sample_qubo(qubo, num_repeats=500)
#レスポンスの確認
print('response')
for (sample, energy, occurrence) in response.data():
print(f'Sample:{list(sample.values())} Energy:{energy} Occurrence:{occurrence}')
#1になった量子ビット番号
ans = np.where(np.array(list(sample.values())) == 1)[0]
print(ans)offset
30.0
response
Sample:[0, 1, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0] Energy:-30.0 Occurrence:373
[ 1 3 4 10 12 18 24 25 26 27]
Sample:[0, 1, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0] Energy:-28.0 Occurrence:16
[ 1 3 4 11 12 18 24 25 26 27]
Sample:[0, 1, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 1, 0, 1, 0] Energy:-28.0 Occurrence:20
[ 1 3 4 10 12 19 25 26 27 29]エネルギーがマイナスオフセットと一致する解が得られました。すべての条件を満たしたことを示しています。1になった量子ビット番号を確認すると模範解答の通りであることが分かります。
さいごに
今回は数字の接続箇所に量子ビットを割り当てるのがポイントした。