やること
もうQUBOでペンシルパズルを解くのは終わりにしようかと思いましたが、ナンバーリンク(Numberlink)が解けることに気がついたので追加収録します。
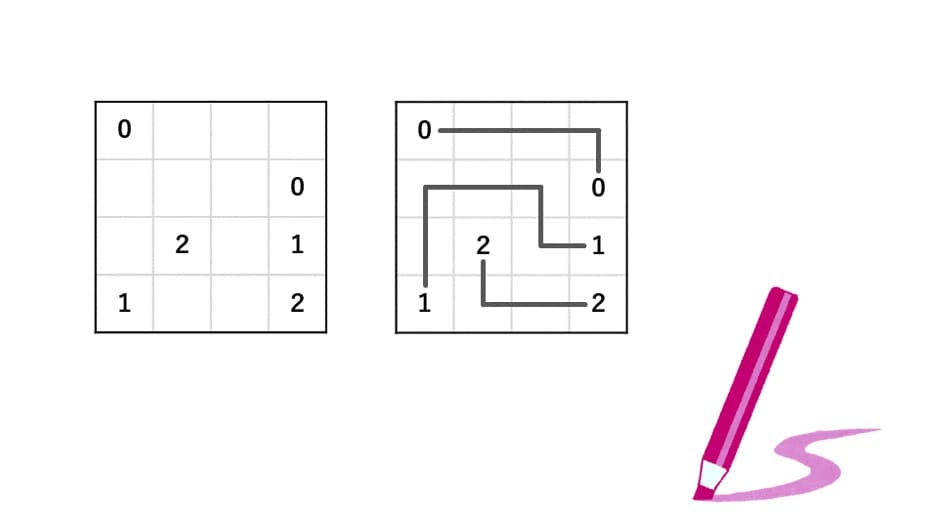
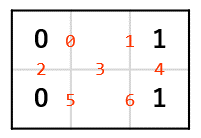
このような問題です。
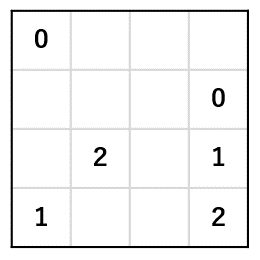
答えはこちらです。
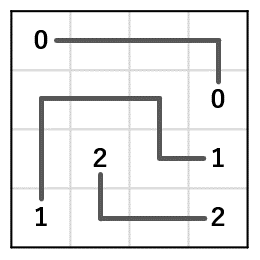
なおナンバーリンクはWikipediaによると
多くのペンシルパズルと違い、ナンバーリンクは完全な理詰めでは解けないことが多く、勘で解けることも多い。理詰めで解けないことから、パズル誌でも稀に別解がある問題が掲載されることがある。
Wikipedia「ナンバーリンク」
とのことで、組合せ最適化や量子アニーリングが適していると解釈できる気がします。
おさらい
今回は
基本「n個の量子ビットからm個を1にする」
応用A3「2個の量子ビットが同時に1になったら報酬を与える」
を使用します。
その他のQUBOで設定できる条件式については過去のまとめ記事をご参照ください↓
どうやってナンバーリンクを解くか?
説明のために簡単な問題を用意しました。
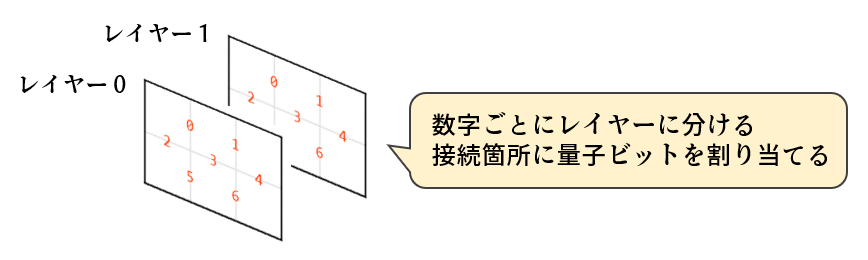
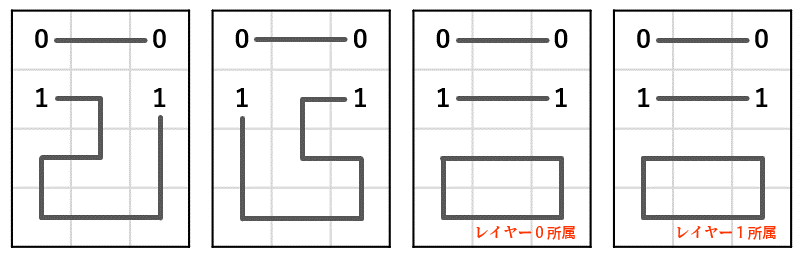
数字ごとにレイヤーに分け、マスの接続箇所に量子ビットを割り当てます。全部で14量ビット使うことになります。量子ビットが1になれば、そこを線が通ることになります。
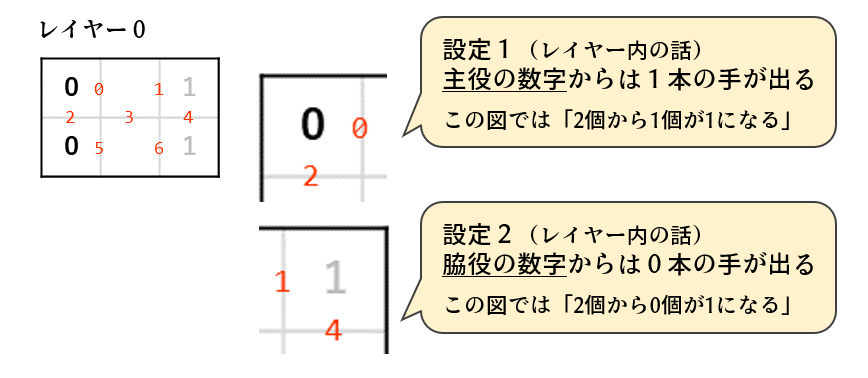
まずレイヤー内に着目します。レイヤー0においては、主役の数字である0からは必ず1本の手が出ます(設定1)。一方、脇役の数字である1からは1本も手が出ません(設定2)。これらを「n個の量子ビットからm個を1にする」を使って設定します。
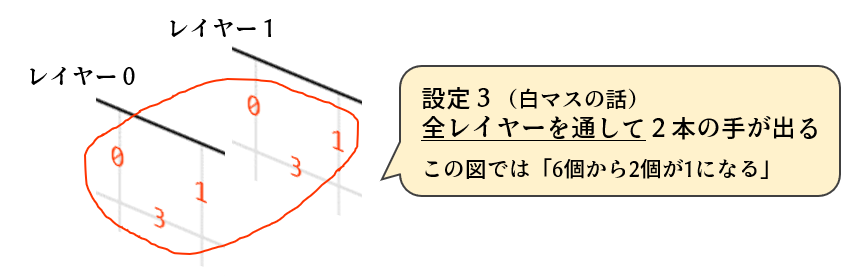
次に白マスに着目します。白マスは線が通過するため必ず2本の手が出るのですが、これは全レイヤーを通して2本の手が出る必要があります(設定3)。例えばレイヤー0の中で2本の手が出ていれば、その線は0から伸びた線を意味します。しかし、レイヤー0で1本、レイヤー1で1本のように分散してしまうかもしれません。
そこで、同一レイヤー内で2本の手が出やすくなる設定をします。同一レイヤー内で [0, 1], [0, 3], [1, 3] のいずれかのペアが同時に1になった場合に報酬を与えます(設定4)。ただしこのままでは [0, 1, 3] すべてが1になって報酬をがっぽり稼いでしまいます(=設定3が破られる)。ですからこの設定4は上記の設定3よりも重みを弱く設定する必要があります(重み0.1)。

簡単な問題のコードと結果
量子ビット名がちょっと特殊ですみません。「q0_02」はレイヤー0の2番接続を表します。
import numpy as np
from pyqubo import Binary
from dwave_qbsolv import QBSolv
#量子ビットを用意する
q0_00 = Binary('q0_00')
q0_01 = Binary('q0_01')
q0_02 = Binary('q0_02')
q0_03 = Binary('q0_03')
q0_04 = Binary('q0_04')
q0_05 = Binary('q0_05')
q0_06 = Binary('q0_06')
q1_00 = Binary('q1_00')
q1_01 = Binary('q1_01')
q1_02 = Binary('q1_02')
q1_03 = Binary('q1_03')
q1_04 = Binary('q1_04')
q1_05 = Binary('q1_05')
q1_06 = Binary('q1_06')
#レイヤー0の主役数字マス、1本出る
H = 0
H += (q0_00 + q0_02 - 1)**2
H += (q0_02 + q0_05 - 1)**2
#レイヤー0の脇役数字マス、0本出る
H += (q0_01 + q0_04 - 0)**2
H += (q0_04 + q0_06 - 0)**2
#レイヤー1の主役数字マス、1本出る
H += (q1_01 + q1_04 - 1)**2
H += (q1_04 + q1_06 - 1)**2
#レイヤー1の脇役数字マス、0本出る
H += (q1_00 + q1_02 - 0)**2
H += (q1_02 + q1_05 - 0)**2
#白マス、全レイヤーを通して2本出る
H += (q0_00 + q0_01 + q0_03 + q1_00 + q1_01 + q1_03 - 2)**2
H += (q0_03 + q0_05 + q0_06 + q1_03 + q1_05 + q1_06 - 2)**2
#レイヤー0の白マス、2本同時に1なら報酬(重み0.1)
H += -0.1 * (q0_00 * q0_01)
H += -0.1 * (q0_00 * q0_03)
H += -0.1 * (q0_01 * q0_03)
H += -0.1 * (q0_03 * q0_05)
H += -0.1 * (q0_03 * q0_06)
H += -0.1 * (q0_05 * q0_06)
#レイヤー1の白マス、2本同時に1なら報酬(重み0.1)
H += -0.1 * (q1_00 * q1_01)
H += -0.1 * (q1_00 * q1_03)
H += -0.1 * (q1_01 * q1_03)
H += -0.1 * (q1_03 * q1_05)
H += -0.1 * (q1_03 * q1_06)
H += -0.1 * (q1_05 * q1_06)
#コンパイル
model = H.compile()
qubo, offset = model.to_qubo()
print(f'offset\n{offset}')
#分割サンプリング
response = QBSolv().sample_qubo(qubo, num_repeats=500)
#レスポンスの確認
print('response')
for (sample, energy, occurrence) in response.data():
print(f'Sample:{list(sample.values())} Energy:{energy} Occurrence:{occurrence}')
#1になった量子ビット番号
ans0 = np.where(np.array(list(sample.values()))[:7] == 1)[0]
ans1 = np.where(np.array(list(sample.values()))[7:] == 1)[0]
print(0, ans0)
print(1, ans1)offset
12.0
response
Sample:[0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1] Energy:-12.2 Occurrence:118
0 [2]
1 [1 3 6]
Sample:[1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0] Energy:-12.2 Occurrence:381
0 [0 3 5]
1 [4]2通りの解が出ました。エネルギーはマイナスオフセット+弱報酬2回分(白マスが2個なので)。最適解だと思います。1になった量子ビット番号から線を復元すると以下の通りです。
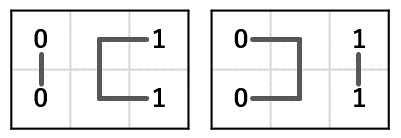
冒頭の問題の結果
さて、条件式が多いのでコードは割愛しますが、同じことを冒頭の問題でもやってみた結果です。
offset
46.0
response
Sample:[1, 1, 1,...,0, 1, 1] Energy:-47.0 Occurrence:170
0 [0 1 2 6]
1 [ 7 8 10 12 16 17]
2 [18 22 23]
Sample:[1, 0, 0,...,0, 1, 1] Energy:-46.8 Occurrence:5
0 [0 6]
1 [ 2 4 5 7 10 12 16 17]
2 [18 22 23]
Sample:[1, 0, 1,...,0, 1, 1] Energy:-46.8 Occurrence:18
0 [ 0 2 4 5 6 12]
1 [ 7 10 16 17]
2 [18 22 23]こちらも模範解答の通りになりました!
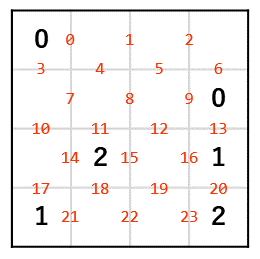

さいごに
今回の内容で一般的なナンバーリンクは解けると思います。ただ、次のようにけっこう遠回りする必要がある問題ではおかしなことが起こります(起こりました)。
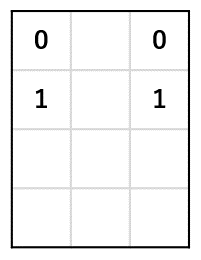
これを解消する設定がなかなか難しい。以前、「スリザーリンク」や「ごきげんななめ」が解けないと言っていたのも同じ理由です。布団に入ってこれを考えていると2分で眠れます。