やること
さあ、いよいよQUBOのラスボスと言っても過言ではないナップサック問題を解いてみましょう。いつもならナップサック問題の最小問題を用意するのですが、まあラスボスだから発展的な内容にしてやってもええかということで、少し難しい「重複を許して取れる」パターンの最小問題を用意しました。
問題は初代タマムシデパートからお送りします!(年齢層よ)
所持金750円でおいしいみず、サイコソーダ、ミックスオレを買うとき、回復量がもっとも多くなる組み合わせを求めてください。ただし重複購入OKとします。
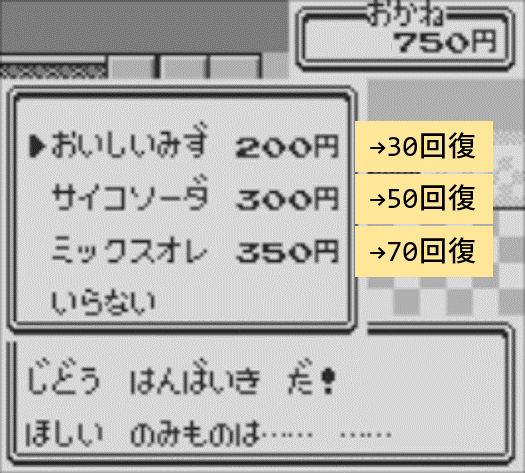
※余談ですが、初代では回復量はそれぞれ50, 60, 80でした。後に調整が入って30, 50, 70になりました。この問題では調整後の回復量を使用します。
おさらい
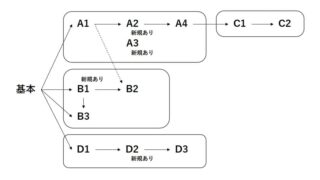
ラスボスと言ったのは応用の条件設定がモリモリだからです。予習の説明をしていると長くなってしまうので、
応用C2「すべての量子ビットを降順にする」
応用D3 解が0と1だけの不等式
まで過去のまとめ記事で予習しておいてください。
これらに加えて、「報酬ができるだけ多くなるように」というコストの考え方(これ重要なのにまとめ記事に入れてない件)、条件間の重み付けも用います。
前半戦:750円ピッタリで買う場合
まず、全体像を掴むために「750円ピッタリで買う」バージョンを解いてみます。
準備1
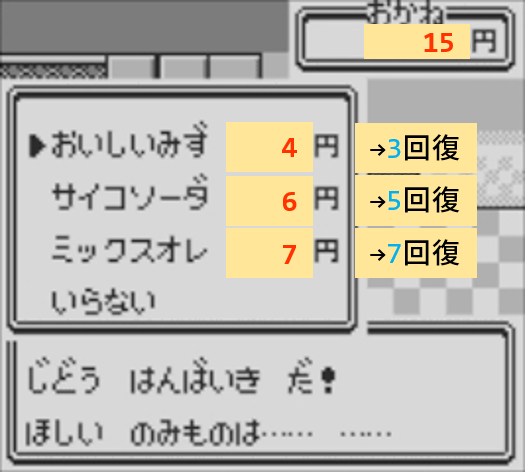
まず問題の数字を簡単にします。金額は50で割り、回復量は10で割りました。数字のオーダーをだいたい揃えておくことで条件間の重みバランスの設定が簡単になったり、特に所持金を750から15にしたことで後半戦で出てくる不等式が考えやすくなります。
準備2
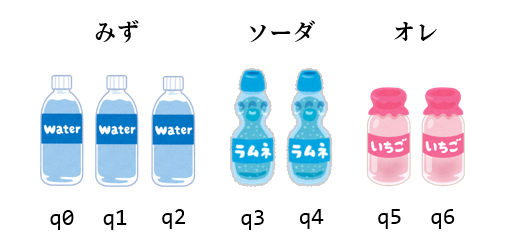
重複を許して購入するため、おいしいみずは最大3個、サイコソーダは2個、ミックスオレは2個に分身させて量子ビットを割り当てます。1になったら買う、0になったら買わない、という意味です。
条件式1(強い条件)
7個のドリンクをそれぞれ取るか取らないかして、合計金額が15になる設定をします。取るは1、取らないは0であり、1のときに金額の係数が有効になってその合計が15になります。
H += (4*q0 + 4*q1 + 4*q2 + 6*q3 + 6*q4 + 7*q5 + 7*q6 - 15)**2条件式2(弱い条件)
あとは「回復量ができるだけ多くなるように」を設定します。7個のドリンクをそれぞれ取るか取らないかして、合計回復量を報酬にします。報酬なので全体にかかる係数はマイナスで、「できるだけ~になるように」は弱い条件なので0.1、これらを合体して-0.1をかけています。
H += -0.1 * (3*q0 + 3*q1 + 3*q2 + 5*q3 + 5*q4 + 7*q5 + 7*q6)前半戦:コードと結果
少し難しいのでサンプリング数を1000回にしています。
from pyqubo import Binary
from dwave_qbsolv import QBSolv
#量子ビットを用意する
q0 = Binary('q0')
q1 = Binary('q1')
q2 = Binary('q2')
q3 = Binary('q3')
q4 = Binary('q4')
q5 = Binary('q5')
q6 = Binary('q6')
#7個のドリンクをそれぞれ取るか取らないか、値段を係数にして合計が15になる(強い条件)
H = 0
H += (4*q0 + 4*q1 + 4*q2 + 6*q3 + 6*q4 + 7*q5 + 7*q6 - 15)**2
#7個のドリンクをそれぞれ取るか取らないか、回復量を係数にして報酬とする(弱い条件)
H += -0.1 * (3*q0 + 3*q1 + 3*q2 + 5*q3 + 5*q4 + 7*q5 + 7*q6)
#コンパイル
model = H.compile()
qubo, offset = model.to_qubo()
print(f'offset\n{offset}')
#分割サンプリング
response = QBSolv().sample_qubo(qubo, num_repeats=1000)
#レスポンスの確認
print('response')
for (sample, energy, occurrence) in response.data():
print(f'Sample:{list(sample.values())} Energy:{energy} Occurrence:{occurrence}')offset
225.0
response
Sample:[0, 1, 1, 0, 0, 1, 0] Energy:-226.3 Occurrence:193
Sample:[1, 1, 0, 0, 0, 0, 1] Energy:-226.3 Occurrence:143
Sample:[1, 1, 0, 0, 0, 1, 0] Energy:-226.3 Occurrence:223
Sample:[1, 0, 1, 0, 0, 0, 1] Energy:-226.3 Occurrence:129
Sample:[0, 1, 1, 0, 0, 0, 1] Energy:-226.3 Occurrence:139
Sample:[1, 0, 1, 0, 0, 1, 0] Energy:-226.3 Occurrence:174ベストな解が6通り出ましたが実質1通りで、みず2本、ソーダ0本、オレ1本です。マイナスオフセットより1.3低いエネルギーなので報酬が1.3、つまり回復量13と分かります。
さて、果たしてこれが最適解でしょうか?
後半戦:750円以内で買う場合
いよいよ本来の問題「750円以内で買う(→15円以内で買う)」を考えます。さらに、解を一つに絞る設定も加えて究極完全態グレート・モスにします。(年齢層よ)
条件式3(超強い条件)
ナップサック問題の鬼門がここです。応用D3の条件式をしっかり予習しておきましょう。
合計金額が15以内になるということは、0, 1, 2, …, 15まで16個の整数のどれかになるということです。そのために補助ビットを16個用意しても良いのですが、もう少し節約できないか考えてみます。合計金額が11以下のとき、おいしいみずを4円で買えばより良い解になります。したがって合計金額は12, 13, 14, 15の4通りしか取り得ません。
以上より、合計金額が「12, 13, 14, 15のどれかになる」ように補助ビットを4個使って設定します。かつ、この条件は条件式1よりもさらに優先しなければならないため(伝われ)、超強い条件として係数10をかけることにします。
#補助ビットを1つだけ1にする
#これにより (12*s0 + 13*s1 + 14*s2 + 15*s3) で 「12 or 13 or 14 or 15」 を表現できる
H += 10 * (s0 + s1 + s2 + s3 - 1)**2これを利用して条件式1を微修正します。7個のドリンクをそれぞれ取るか取らないかして、合計金額を「12 or 13 or 14 or 15」にします。
H += (4*q0 + 4*q1 + 4*q2 + 6*q3 + 6*q4 + 7*q5 + 7*q6 - (12*s0 + 13*s1 + 14*s2 + 15*s3))**2条件式4(なくてもいいので強さはテキトー)
重複を許す問題の宿命ですが、解が複数に分身して出てきます。そこで、例えばおいしいみずを2本買うのであれば [1, 1, 0] のように降順のパターンだけが得られる設定をします。複数の量子ビットを降順にする応用C2を使用します。
H += (1 - q0) * q1
H += (1 - q1) * q2後半戦:コードと結果
もう少しの辛抱です。
from pyqubo import Binary
from dwave_qbsolv import QBSolv
#量子ビットを用意する
q0 = Binary('q0')
q1 = Binary('q1')
q2 = Binary('q2')
q3 = Binary('q3')
q4 = Binary('q4')
q5 = Binary('q5')
q6 = Binary('q6')
#補助ビットを用意する
s0 = Binary('s0')
s1 = Binary('s1')
s2 = Binary('s2')
s3 = Binary('s3')
#補助ビットを1つだけ1にする(超強い条件)
#これにより (12*s0 + 13*s1 + 14*s2 + 15*s3) で 「12 or 13 or 14 or 15」 を表現できる
H = 0
H += 10 * (s0 + s1 + s2 + s3 - 1)**2
#7個のドリンクをそれぞれ取るか取らないか、値段を係数にして合計が「12 or 13 or 14 or 15」になる(強い条件)
H += (4*q0 + 4*q1 + 4*q2 + 6*q3 + 6*q4 + 7*q5 + 7*q6 - (12*s0 + 13*s1 + 14*s2 + 15*s3))**2
#7個のドリンクをそれぞれ取るか取らないか、回復量を係数にして報酬とする(弱い条件)
H += -0.1 * (3*q0 + 3*q1 + 3*q2 + 5*q3 + 5*q4 + 7*q5 + 7*q6)
#おいしいみずを降順にする
H += (1 - q0) * q1
H += (1 - q1) * q2
#サイコソーダを降順にする
H += (1 - q3) * q4
#ミックスオレを降順にする
H += (1 - q5) * q6
#コンパイル
model = H.compile()
qubo, offset = model.to_qubo()
print(f'offset\n{offset}')
#分割サンプリング
response = QBSolv().sample_qubo(qubo, num_repeats=1000)
#レスポンスの確認
print('response')
for (sample, energy, occurrence) in response.data():
print(f'Sample:{list(sample.values())} Energy:{energy} Occurrence:{occurrence}')offset
10.0
response
Sample:[0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0] Energy:-11.4 Occurrence:11
Sample:[1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1] Energy:-11.3 Occurrence:30
Sample:[0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0] Energy:-11.2 Occurrence:2
Sample:[1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0] Energy:-11.1 Occurrence:19ベストな解が1通り出ました。みず0本、ソーダ0本、オレ2本で、後ろの4つは補助ビットです。マイナスオフセットより1.4低いエネルギーなので回復量14に上がりました。補助ビットの右から2つ目が立っていることから、合計金額は15ではなく14と分かります。全額使わないというのが面白いですね!
さいごに
以上、みず0本、ソーダ0本、オレ2本で合計金額700円(残金50円)、合計回復量は140でした。
この内容が理解できればQUBOマスターも近いのではないでしょうか!?(しらんけど)