21-29. 量子アニーリング（QUBO）でクラスタリング

量子コンピュータ

2023/06/04

やること
おさらい
どうやってクラスタリングするのか？
コード
さいごに

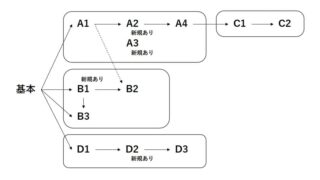
やること

もうQUBOという字を見るだけで食欲がなくなるくらい飽きていますが、まだクラスタリングを試していないことに気がつきました。QUBOでクラスタリングしてみましょう。

この10点を３クラスに分割してみます。

おさらい

今回は

One-hotエンコーディング

応用A2「2個の量子ビットが同時に1になったらペナルティを与える」

を使用します。これらQUBOで設定できる条件式については過去のまとめ記事をご参照ください↓

どうやってクラスタリングするのか？

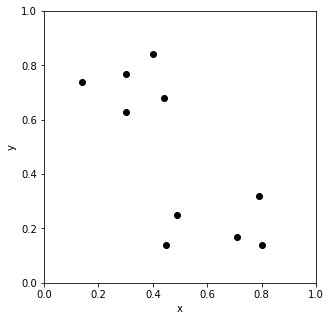
この10点を３クラスに分割してみましょう。

x = np.array([0.45, 0.80, 0.71, 0.49, 0.79, 0.30, 0.44, 0.14, 0.30, 0.40])
y = np.array([0.14, 0.14, 0.17, 0.25, 0.32, 0.63, 0.68, 0.74, 0.77, 0.84])

まず、各点に３個ずつ量子ビットを割り当ててワンホットとします。例えば、点0は [q0_1, q0_2, q0_3] の３つで表し、q0_1が１になればクラス１といった具合です。ワンホットなので「３個の量子ビットから１個を１にする」を設定します。

次に、２点間の距離に応じた設定をします。以下参照。

「同じクラスに属する点は互いの距離が小さい」というのがクラスタリングの目標です。そこで、ある２点が同じクラスになった場合、その距離に比例したペナルティを加算します。アニーリングでペナルティが最小の解を探すことは、クラス内の相互距離が最小となるクラス分けを探すことに相当するわけです。

「距離ができるだけ小さくなるように」は「できるだけ～になるように」系なので弱い条件です。重み0.1をかけてください。

コード

条件式が多いのでfor文を使っていますが、式はprint()で表示されるのでよく確認してください。

from pyqubo import Binary
from dwave_qbsolv import QBSolv
import numpy as np
import matplotlib.pyplot as plt


#データ
x = np.array([0.45, 0.80, 0.71, 0.49, 0.79, 0.30, 0.44, 0.14, 0.30, 0.40])
y = np.array([0.14, 0.14, 0.17, 0.25, 0.32, 0.63, 0.68, 0.74, 0.77, 0.84])

#グラフ確認
plt.plot(x, y, 'o')
plt.xlabel('x'); plt.ylabel('y')
plt.show()


#量子ビットを用意する、例：q0_1は点0のワンホットクラス1
for i in range(10):
    for n in range(1, 4):
        command = f'q{i}_{n} = Binary(\'q{i}_{n}\')'
        print(command)
        exec(command)

#各点ともワンホットで一つだけ１になる
H = 0
for i in range(10):
    command = f'H += (q{i}_1 + q{i}_2 + q{i}_3 - 1)**2'
    print(command)
    exec(command)

#2点の組み合わせで
for i in range(9):
    for j in range(i+1, 10):
        #2点の距離
        dist = ((x[i] - x[j])**2 + (y[i] - y[j])**2)**0.5
        
        #同時にクラス1に入った場合のペナルティ
        command = f'H += 0.1 * {dist} * (q{i}_1 * q{j}_1)'
        print(command)
        exec(command)
        
        #同時にクラス2に入った場合のペナルティ
        command = f'H += 0.1 * {dist} * (q{i}_2 * q{j}_2)'
        print(command)
        exec(command)
        
        #同時にクラス3に入った場合のペナルティ
        command = f'H += 0.1 * {dist} * (q{i}_3 * q{j}_3)'
        print(command)
        exec(command)


#コンパイル
model = H.compile()
qubo, offset = model.to_qubo()

#分割サンプリング
response = QBSolv().sample_qubo(qubo, num_repeats=500)

#レスポンスの確認
print('response')
for (sample, energy, occurrence) in response.data():
    print(f'Sample:{list(sample.values())} Energy:{energy} Occurrence:{occurrence}')
    
    #ワンホットから整数に戻して確認
    tmp = np.array(list(sample.values())).reshape(10, 3)
    ans = np.zeros(10, int)
    for i in range(10):
        ans[i] = np.argmax(tmp[i, :]) + 1
    print(ans)
    
    #グラフ確認
    plt.plot(x[ans==1], y[ans==1], 'o', label='1')
    plt.plot(x[ans==2], y[ans==2], 'o', label='2')
    plt.plot(x[ans==3], y[ans==3], 'o', label='3')
    plt.xlabel('x'); plt.ylabel('y')
    plt.legend()
    plt.show()

response
Sample:[0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1] Energy:-9.75216673811864 Occurrence:118
[2 1 1 2 1 3 3 3 3 3]
Sample:[1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1] Energy:-9.75216673811864 Occurrence:102
[1 2 2 1 2 3 3 3 3 3]
Sample:[0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0] Energy:-9.75216673811864 Occurrence:35
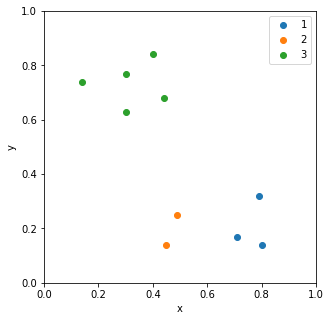
[3 1 1 3 1 2 2 2 2 2]

最良の解は６通り出てきますが、３クラスが入れ替わっただけなので実質１パターンです。ワンホットをクラス番号に戻してグラフで確認すると、適切に分割できていることが分かります。