やること
2024/09/07追記
試験問題の役割を終えたため解答の一例を公開しました。
「TYTAN」パッケージのチュートリアルを終えて「qubomaster」認定試験を受ける人が少しずつ増えてきました。
「もっと難しい問題を!」という声が聞こえてきたので(嘘)、実力テスト4として高校物理の問題を用意しました。
TYTANについて
「TYTAN」はOSSのアニーリングSDKです。
筆者はチュートリアルコースを担当しています。
discordコミュニティもあるので気軽に質問できます。どなたでも参加できます → https://discord.gg/qT5etstPW8
チュートリアルを終えて試験に合格するとblueqat社が認定する「qubomaster」という資格が与えられます。qubomasterになると(blueqatサイト上で)認定バッジが付与され、有償業務の受託可能者リストに入ります。
おさらい
QUBOで設定できる条件式についてはこちらの記事にまとめてあります。暗記する必要はありませんが概要は把握しておくと良さそうです。
これまでのQUBOアニーリング系の記事はサイドバーの「カテゴリ一覧」→「量子コンピュータ」から絞れます。
実力テスト問題4
問1
自然長が1、ばね定数が1の軽いばねが2個ある。
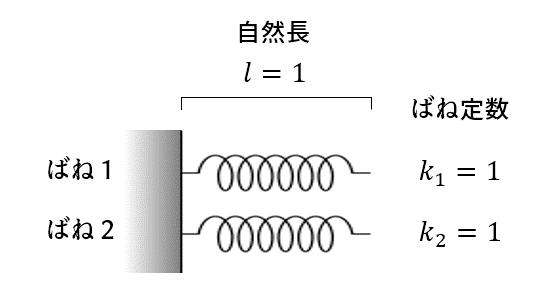
この2個のばねを直列につなげ、幅3の壁の隙間にひっかけた。
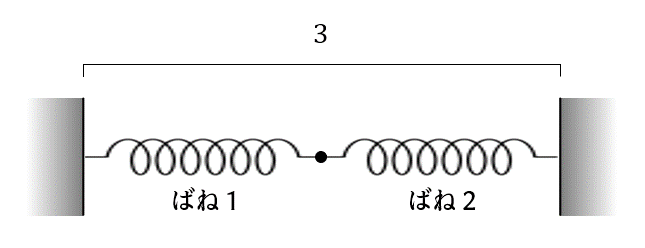
このときの各ばねの長さを求めよ。なお、ばね定数kのばねが自然長から長さxだけ伸縮したときの弾性力はkxである。各ばねの「長さ」または「伸縮分の長さ」のどちらを求めても良い。
問2
自然長が1の軽いばねが4個ある。それぞれのばね定数は1, 2, 3, 4である。
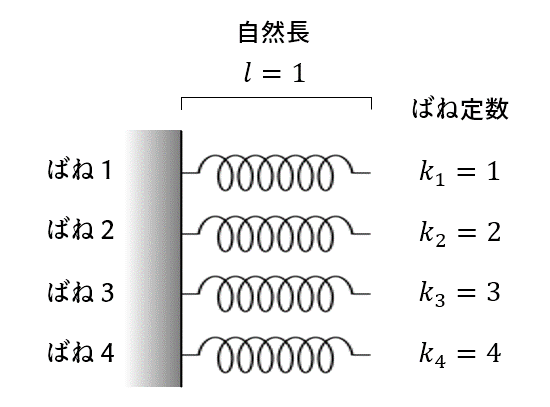
この4個のばねを直列につなげ、幅5の壁の隙間にひっかけた。
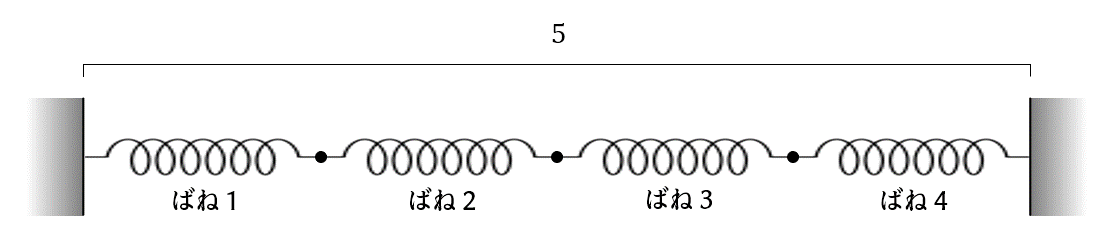
このときの各ばねの長さを小数点以下3桁まで求めよ。各ばねの「長さ」または「伸縮分の長さ」のどちらを求めても良い。
提出方法、注意事項など
解答は、そのまま実行するだけのpythonコードを「.py」または「.ipynb」のファイル形式で以下フォームから提出してください。すぐに自動返信メールが届きます。
※100KBまでの.py, .ipynbファイルのみ受け付けます
※受付完了メールが自動送信されます
▼注意事項
- テキスト欄やコメントアウトにより最低限の説明や思考過程を含めてください
- その際、チュートリアルの「おすすめコース」のどれと関連があるかにも触れてください
- 説明のための図は必ずしも必要ありません
- アニーリングのソルバーには必ずTYTANパッケージを使用してください
- 必ずしも1回の実行で正解が得られる必要はなく、正解が得られることが期待できるコードであれば問題ありません
▼合格条件
- QUBO条件式が妥当であること
- 説明や思考過程が妥当であること
- 十分な可読性のPythonコードであること
- チュートリアル「おすすめコース」を把握していること
解答の一例(2024/09/07追記)
問1
ばね1が自然長から伸びた長さをx、ばね2が自然長から伸びた長さをyとする。幅3の隙間にひっかけたため長さの条件は「x + y = 1」。また、2つのばねの張力が等しいことから「k1x = k2y」。これらを連立方程式として解く。
pip install tytanfrom tytan import *
#ばね定数
k1 = 1
k2 = 1
#量子ビットをNビット表現で用意する
x = symbols_nbit(0, 1, 'x{}', num=8)
y = symbols_nbit(0, 1, 'y{}', num=8)
print(x)
#連立方程式の設定
H = 0
H += (x + y - 1)**2
H += (k1*x - k2*y)**2
#コンパイル
qubo, offset = Compile(H).get_qubo()
print(f'offset = {offset}')
#サンプラー選択
solver = sampler.SASampler()
#サンプリング
result = solver.run(qubo, shots=100)
#上位3件
for r in result[:3]:
print(r)
print('x =', Auto_array(r[0]).get_nbit_value(x))
print('y =', Auto_array(r[0]).get_nbit_value(y))0.5*x0 + 0.25*x1 + 0.125*x2 + 0.0625*x3 + 0.03125*x4 + 0.015625*x5 + 0.0078125*x6 + 0.00390625*x7
offset = 1.0
Energy -1.0, Occurrence 24
x = 0.5
y = 0.5
Energy -0.999969482421875, Occurrence 22
x = 0.49609375
y = 0.5
Energy -0.999969482421875, Occurrence 24
x = 0.5
y = 0.49609375よってx = 0.5、y = 0.5。
問2
こちらも考え方は同じ。
from tytan import *
#ばね定数
k1 = 1
k2 = 2
k3 = 3
k4 = 4
#量子ビットをNビット表現で用意する
x = symbols_nbit(0, 1, 'x{}', num=11)
y = symbols_nbit(0, 1, 'y{}', num=11)
z = symbols_nbit(0, 1, 'z{}', num=11)
w = symbols_nbit(0, 1, 'w{}', num=11)
print(x)
#連立方程式の設定
H = 0
H += (x + y + z + w - 1)**2
H += (k1*x - k2*y)**2
H += (k2*y - k3*z)**2
H += (k3*z - k4*w)**2
#コンパイル
qubo, offset = Compile(H).get_qubo()
print(f'offset = {offset}')
#サンプラー選択
solver = sampler.ArminSampler()
#サンプリング
result = solver.run(qubo, shots=10000)
#上位3件
for r in result[:3]:
print(r)
print('x =', Auto_array(r[0]).get_nbit_value(x))
print('y =', Auto_array(r[0]).get_nbit_value(y))
print('z =', Auto_array(r[0]).get_nbit_value(z))
print('w =', Auto_array(r[0]).get_nbit_value(w))0.5*x0 + 0.25*x1 + 0.00048828125*x10 + 0.125*x2 + 0.0625*x3 + 0.03125*x4 + 0.015625*x5 + 0.0078125*x6 + 0.00390625*x7 + 0.001953125*x8 + 0.0009765625*x9
offset = 1.0
MODE: GPU
DEVICE: cuda:0
Energy -0.9999995231628418, Occurrence 6
x = 0.47998046875
y = 0.240234375
z = 0.16015625
w = 0.1201171875
Energy -0.9999990463256836, Occurrence 4
x = 0.48046875
y = 0.240234375
z = 0.16015625
w = 0.1201171875
Energy -0.9999988079071045, Occurrence 7
x = 0.4794921875
y = 0.23974609375
z = 0.16015625
w = 0.1201171875小数点第4位を四捨五入してx = 0.480、y = 0.240、z = 0.160、w = 0.120となる。
解が小数点以下3桁まで正しいことを説明する。小数点第3位を正しく得るには、小数点第4位を四捨五入することを考慮するとxの刻み幅が0.0005未満であれば十分である。xを11ビットで定義したことで刻み幅が1/2048≒0.000488になるため、四捨五入したときに求めたい小数点第3位の値を飛び越すことなく得ることができる。(より厳密には10ビットでも十分だが・・・)
<この問題のポイント>
単純な力学の問題だが、量子ビットの二進数表現を扱えるかどうか、値の精度保証ができるかが問われている。ちなみに10ビットで計算するとfloatの誤差のせいか良くない解が混ざってくるのでややこしい(困った)。