やること
2024/09/07追記
試験問題の役割を終えたため解答の一例を公開しました。
以前、「Prolog」でグラコロバーガーの合成経路を探索したことがありました。これを改造してQubomaster認定試験のための実力テスト5を作りましたので、挑戦してみてください。
TYTANについて
「TYTAN」はOSSのアニーリングSDKです。
筆者はチュートリアルコースを担当しています。
discordコミュニティもあるので気軽に質問できます。どなたでも参加できます → https://discord.gg/qT5etstPW8
チュートリアルを終えて試験に合格するとblueqat社が認定する「qubomaster」という資格が与えられます。qubomasterになると(blueqatサイト上で)認定バッジが付与され、有償業務の受託可能者リストに入ります。

おさらい
QUBOで設定できる条件式についてはこちらの記事にまとめてあります。暗記する必要はありませんが概要は把握しておくと良さそうです。
これまでのQUBOアニーリング系の記事はサイドバーの「カテゴリ一覧」→「量子コンピュータ」から絞れます。
実力テスト問題5
グラコロバーガーの合成経路は次のとおりである。図中の数字は工程にかかる時間を表す。グラコロバーガー合成におけるクリティカルパス(律速経路)を求めよ。
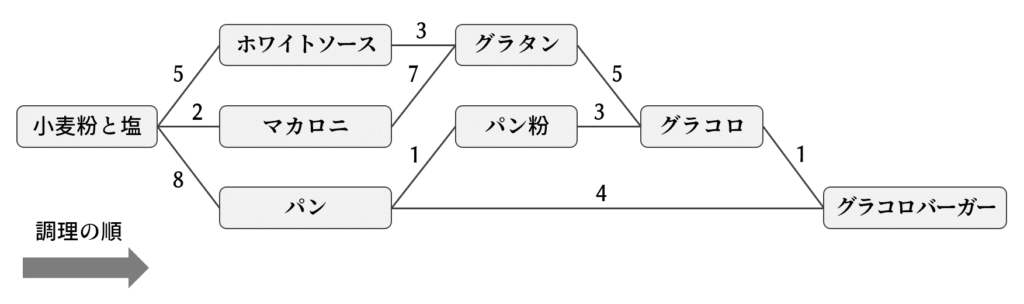

クリティカルパスはもっとも長い時間がかかる一本の経路のことである。なお、調理は左から右へ一方向でしか進めない。
補足(2023/08/06追記)
取り得る経路は4つしかないが、4つの経路を列挙することは禁止とする。(問題を拡張した際に、経路の列挙が組合せ爆発に当たるため)。
提出方法、注意事項など
解答は、そのまま実行するだけのpythonコードを「.py」または「.ipynb」のファイル形式で以下フォームから提出してください。すぐに自動返信メールが届きます。
※100KBまでの.py, .ipynbファイルのみ受け付けます
※受付完了メールが自動送信されます
▼注意事項
- テキスト欄やコメントアウトにより最低限の説明や思考過程を含めてください
- その際、チュートリアルの「おすすめコース」のどれと関連があるかにも触れてください
- 説明のための図は必ずしも必要ありません
- アニーリングのソルバーには必ずTYTANパッケージを使用してください
- 必ずしも1回の実行で正解が得られる必要はなく、正解が得られることが期待できるコードであれば問題ありません
▼合格条件
- QUBO条件式が妥当であること
- 説明や思考過程が妥当であること
- 十分な可読性のPythonコードであること
- チュートリアル「おすすめコース」を把握していること
解答の一例(2024/09/07追記)
各エッジに量子ビットを割り当てる。

制約条件はスタートから1本の線で繋いでいくということ。言い換えると「各ノードの前後の手の数が等しい」。例えばグラタンの前の手が0本であれば後ろも必ず0本である。前の手が1本であれば(=グラタンまで線が来ていれば)後ろも必ず1本である(グラタンから線が出る)。あとは採用したエッジのコスト報酬を設定すれば一番重いパスが得られるはずだ。
pip install tytanfrom tytan import *
import numpy as np
#エッジの量子ビット
q = symbols_list([10], 'q{}')
print(q)
#採用するエッジの重み合計をコスト(報酬)とする
Hcost = 0
Hcost -= 5 * q[0]
Hcost -= 2 * q[1]
Hcost -= 8 * q[2]
Hcost -= 3 * q[3]
Hcost -= 7 * q[4]
Hcost -= 1 * q[5]
Hcost -= 4 * q[6]
Hcost -= 5 * q[7]
Hcost -= 3 * q[8]
Hcost -= 1 * q[9]
#スタートのエッジから必ず1個採用
Hconst = 0
Hconst += (q[0] + q[1] + q[2] - 1)**2
#各ノードから見たとき、前後の手の数が等しい
Hconst += (q[0] - q[3])**2
Hconst += (q[1] - q[4])**2
Hconst += (q[2] - (q[5] + q[6]))**2
Hconst += ((q[3] + q[4]) - q[7])**2
Hconst += (q[5] - q[8])**2
Hconst += ((q[7] + q[8]) - q[9])**2
#合体
H = Hconst + 0.01*Hcost
print(H)
#コンパイル
qubo, offset = Compile(H).get_qubo()
print(f'offset = {offset}')
#サンプラー選択
solver = sampler.SASampler()
#サンプリング
result = solver.run(qubo)
#上位3件
for r in result[:3]:
print(f'Energy {r[1]}, Occurrence {r[2]}')
arr, subs = Auto_array(r[0]).get_ndarray('q{}')
print(arr)[q0 q1 q2 q3 q4 q5 q6 q7 q8 q9]
offset = 1.0
Energy -1.1499999999999997, Occurrence 34
[0 1 0 0 1 0 0 1 0 1]
Energy -1.14, Occurrence 5
[1 0 0 1 0 0 0 1 0 1]
Energy -1.1300000000000001, Occurrence 52
[0 0 1 0 0 1 0 0 1 1]採用するエッジ [q1, q4, q7, q9] はコスト [2, 7, 5, 1] のパスを意味している。
<この問題のポイント>
この解答例はチュートリアルで学ばなかったパターンを使用しているためとても難しく感じる。チュートリアルの範囲でも、補助ビットを使用して「各ノードから0本または2本出る」のような雰囲気でできないことはないが複雑になってしまう。