21-5. D-waveマシンのいろいろな条件設定まとめ

2023/5/23追記：本記事の内容は大幅にアップデートされています。以下の記事でまとめてあります。
量子アニーリングのQUBOで設定可能な条件式まとめ（保存版）

やること
実行環境
pip, import
基本となる共通コード
おさらい
ｎ個の量子ビットを全部１または全部０にする
ｎ個の量子ビットをｍ個またはm+2個を１にする（失敗編）
ｎ個の量子ビットをｍ個またはm+2個を１にする（解決編）
まとめ

やること

これまでは「ｎ個の量子ビットからｍ個を１にする」という条件設定ができればいろいろな問題が解ける！と思っていましたが、実際にいろいろなパズルを解こうとすると、それだけでは足りないことがわかりました。

ここではD-waveマシンを使いこなすための多彩な条件設定を学びます。

実行環境

WinPython3.6をおすすめしています。

WinPython - Browse /WinPython_3.6/3.6.7.0 at SourceForge.net

Portable Scientific Python 2/3 32/64bit Distribution for Windows

Google Colaboratoryが利用可能です。

Google Colaboratory

pip, import

必要なパッケージをインストールし、

pip install pyqubo
pip install dwave-ocean-sdk

インポートします。

from pyqubo import Binary
from dwave.system.composites import EmbeddingComposite
from dwave.system.samplers import DWaveSampler

基本となる共通コード

ｎ個の量子ビットを用意する

３つの量子ビットを用意するコマンドは次のとおりでした。

#３つの量子ビットを用意する
q0, q1, q2 = Binary('q0'), Binary('q1'), Binary('q2')

D-waveでサンプリングしまくる

その後、条件式を設定してサンプリングしまくる部分のコードはこちらです。

#条件を記述する
H = (条件式)

#コンパイル
model = H.compile()
#print('model\n{}'.format(model))
qubo, offset = model.to_qubo()
#print('qubo\n{}'.format(qubo))

#D-waveの設定
sampler = EmbeddingComposite(DWaveSampler(endpoint='https://cloud.dwavesys.com/sapi',
                                          token='your_token', #あなたのAPIトークンを記入
                                          solver='DW_2000Q_5')) #利用可能なソルバーを指定

#サンプリングしまくる
response = sampler.sample_qubo(qubo, num_reads=1000)

#レスポンスの確認
print('response')
for (sample, energy, occurrence, _) in response.data():
    print('Sample:{} Energy:{} Occurrence:{}'.format(list(sample.values()), energy, occurrence))

おさらい

ｎ個の量子ビットからｍ個を１にする

「３個の量子ビットから２個を１にする」は次のとおりでした。

#条件を記述する
H = (q0 + q1 + q2 - 2)**2

Sample:[1, 1, 0] Energy:-4.0 Occurrence:244
Sample:[0, 1, 1] Energy:-4.0 Occurrence:350
Sample:[1, 0, 1] Energy:-4.0 Occurrence:403
Sample:[1, 0, 1] Energy:-4.0 Occurrence:1
Sample:[1, 0, 0] Energy:-3.0 Occurrence:2

3C2 =３通りが出力されています。どうしてこの設定でうまくいくのかを考えます。

H（ハミルトニアン）は量子ビット全体のエネルギー値みたいなものです。q0～q2はそれぞれ０か１をとります。D-waveは、Hがもっとも低くなるq0～q2の組み合わせを探すためのマシンです。

q0～q2にそれぞれ０か１を適当に代入してみるとH = 0, 1, 4を取りうることがわかります。

H = 0になるのは、q0～q2のうち２個が１のとき
H = 1になるのは、q0～q2のうち１個または３個が１のとき
H = 4になるのは、q0～q2のうち０個が１のとき

ですから、上記の設定では「３個の量子ビットから２個を１にする」組み合わせが得られるのです。

「x = q0 + q1 + q2」と置くと、xはまさに「いくつを１にしたいか」を表しています。条件式は「H = (x – 2)**2」と書けます。

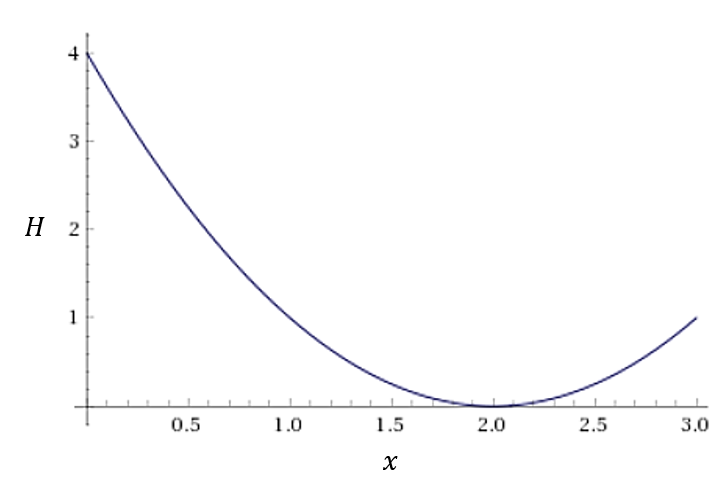
これをプロットしてみると、x = 2が最適解であることが明確にわかります。よって「３個の量子ビットから２個を１にする」が得られるというわけです。

ｎ個の量子ビットからｍ個またはm+1個を１にする

「３個の量子ビットから１個または２個を１にする」は次のとおりでした。

#条件を記述する
H = (q0 + q1 + q2 - 1.5)**2

Sample:[0, 1, 0] Energy:-2.0 Occurrence:167
Sample:[1, 0, 0] Energy:-2.0 Occurrence:185
Sample:[0, 1, 1] Energy:-2.0 Occurrence:154
Sample:[0, 0, 1] Energy:-2.0 Occurrence:166
Sample:[1, 0, 1] Energy:-2.0 Occurrence:180
Sample:[1, 1, 0] Energy:-2.0 Occurrence:148

3C1 + 3C2 =６通りが出力されています。なぜこうなるのかを理解するために、H = (x – 1.5)**2のグラフを見てみます。

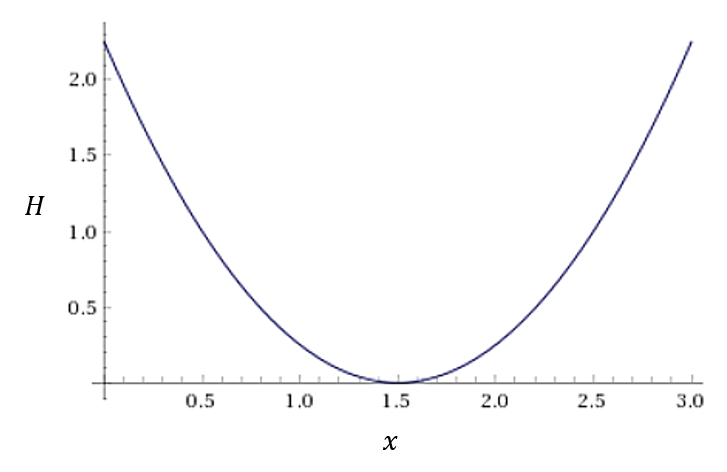
xは0, 1, 2, 3の離散値を取りうるため、x = 1.5はとれず、x = 1, 2が最適解であることがわかります。よって「３個の量子ビットから１個または２個を１にする」ができるのです。

ｎ個の量子ビットを全部１または全部０にする

「３個の量子ビットから０個または３個を１にする」はどうすればよいでしょうか。さっきの式にマイナスを付けてみます。

#条件を記述する
H = - (q0 + q1 + q2 - 1.5)**2

Sample:[1, 1, 1] Energy:0.0 Occurrence:610
Sample:[0, 0, 0] Energy:0.0 Occurrence:390

できました。なぜこれでうまくいくかというと、H = – (x – 1.5)**2のグラフを見ると、

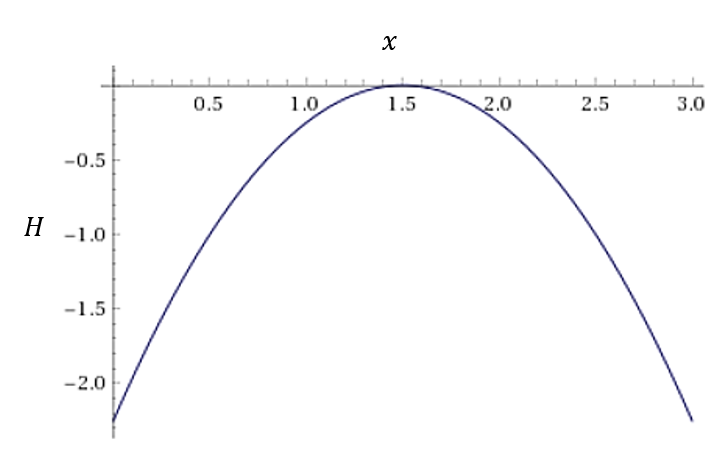
x = 0, 3におけるエネルギー値がもっとも低いからです。

ｎ個の量子ビットをｍ個またはm+2個を１にする（失敗編）

ここからが本番です。「３個の量子ビットから１個または３個を１にする」はどうすればよいでしょうか。

明らかにダメな例

一瞬、「１と３の中間である２を引けばいいんだろう」と思ったのですが、

#条件を記述する
H = (q0 + q1 + q2 - 2)**2

これは「２個を１にする」やつなので、実行するまでもなくダメです。

足してみる

「１個を１にする」と「３個を１にする」を足してみたらどうでしょうか？

#条件を記述する
H = (q0 + q1 + q2 - 1)**2 + (q0 + q1 + q2 - 3)**2

Sample:[1, 0, 1] Energy:-8.0 Occurrence:365
Sample:[1, 1, 0] Energy:-8.0 Occurrence:285
Sample:[0, 1, 1] Energy:-8.0 Occurrence:350

これも「２個を１にする」になってしまいました。なぜかというと、H = (x – 1)**2 + (x – 3)**2のグラフはx = 2で落ち込むからです。

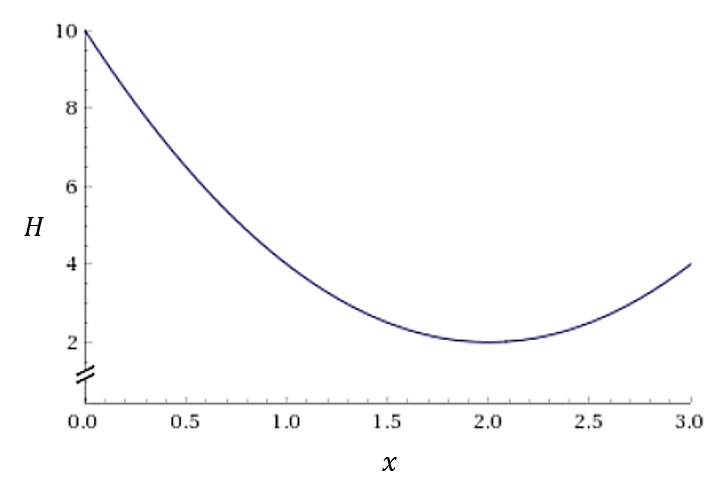
２次関数はどんなに足しても２次関数ですので、足す方法では不可能です。

かけてみる

かけてみたらどうでしょうか？理論上はこれでいけるはずです。

#条件を記述する
H = (q0 + q1 + q2 - 1)**2 * (q0 + q1 + q2 - 3)**2

Sample:[1, 0, 0, 1] Energy:-13.0 Occurrence:31
Sample:[1, 0, 0, 1] Energy:-13.0 Occurrence:12
Sample:[1, 1, 1, 1] Energy:-9.0 Occurrence:1
Sample:[1, 1, 0, 1] Energy:-8.0 Occurrence:616
Sample:[1, 1, 0, 1] Energy:-8.0 Occurrence:243
Sample:[0, 1, 1, 1] Energy:-5.0 Occurrence:97

あれ、いろいろおかしいです。量子ビットは３個しか用意していないのに４個に増えています。解も実行するたびに滅茶苦茶な結果になります。

ちなみに、上の式を展開した

#条件を記述する
H = (q0+q1+q2)**4 - 8*(q0+q1+q2)**3 + 22*(q0+q1+q2)**2 - 24*(q0+q1+q2) + 9

#条件を記述する
H = q0**4 + 4*q0**3*q1 + 4*q0**3*q2 - 8*q0**3 + 6*q0**2*q1**2 + 12*q0**2*q1*q2 - 24*q0**2*q1 \
  + 6*q0**2*q2**2 - 24*q0**2*q2 + 22*q0**2 + 4*q0*q1**3 + 12*q0*q1**2*q2 - 24*q0*q1**2 \
  + 12*q0*q1*q2**2 - 48*q0*q1*q2 + 44*q0*q1 + 4*q0*q2**3 - 24*q0*q2**2 + 44*q0*q2 \
  - 24*q0 + q1**4 + 4*q1**3*q2 - 8*q1**3 + 6*q1**2*q2**2 - 24*q1**2*q2 + 22*q1**2 \
  + 4*q1*q2**3 - 24*q1*q2**2 + 44*q1*q2 - 24*q1 + q2**4 - 8*q2**3 + 22*q2**2 - 24*q2 + 9

も同様にダメでした。

関数の形状はちゃんとx = 1, 3で落ち込んでいるのに、なぜうまく行かないのでしょうか。

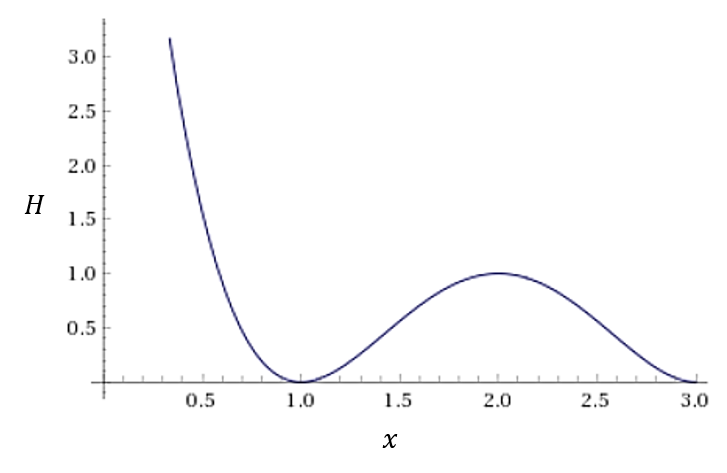
そこで、マシンに投げる前のQUBO（読み方：きゅーぼ）（量子ビット間の重み）を見てみると、

qubo
{('q0', 'q1'): 10.0, ('q0', 'q2'): 5.0, ('q0', 'q0*q2'): -10.0, ('q1', 'q2'): 10.0, ('q0*q2', 'q1'): -12.0, ('q0*q2', 'q2'): -10.0, ('q0', 'q0'): -9.0, ('q1', 'q1'): -9.0, ('q2', 'q2'): -9.0, ('q0*q2', 'q0*q2'): 25.0}

「q0*q2」という謎の補助ビットを用意してくれていることがわかりました。ということは、おそらく[1, 0, 0, 1] = [q0, q0*q2, q1, q2]なので[q0, q1, q2] = [1, 0, 1]しか得られなかったということです。（実行するたびに変わります）

「１個または３個」とは程遠い結果になりました。D-waveマシンはハードウェアの都合上、２量子ビットよりも多くの相互作用を扱うことができません。その場合には補助ビットを用意する必要がありますが、単にＨに条件式を入れる方式ではうまいことやってくれないということが分かりました。

ｎ個の量子ビットをｍ個またはm+2個を１にする（解決編）

2023/5/23追記：この章の内容は大幅にアップデートされているので読まなくて大丈夫です。以下の記事でまとめてあります。
量子アニーリングのQUBOで設定可能な条件式まとめ（保存版）

３個の量子ビットから１個または３個を１にする

泣く泣く、日本最大の（もしかしたら世界最大の？）量子コンピュータのオンラインコミュニティであるSlack「Blueqat（クリックで参加）」で有識者に助けを求めました。

こちらの記事の方法でできるかもよ、と教えていただきました。

D-Waveの制約式をイジングモデルに変換するライブラリの仕組みを追ってみた - Qiita

dwavebinarycsp量子アニーリングマシンD-Waveの dwavebinarycsp というライブラリを使うと、制約式充足問題を二次形式最小化問題すなちイジングモデル（もしくはQUBO）…

結論から書くと、

#５つの量子ビットを用意する
q0, q1, q2, q3, q4 = Binary('q0'), Binary('q1'), Binary('q2'), Binary('q3'), Binary('q4')

#条件を記述する
aux0 = q3 #補助ビット
aux1 = q4 #補助ビット
H = (4.0*aux1)+(6.0*q0)+(-2.0*q1)+(6.0*q2)+(-4.0*aux0*aux1)+(-4.0*aux0*q0)+(4.0*aux0*q1)+(-4.0*aux0*q2)+(-4.0*aux1*q0)+(4.0*aux1*q1)+(-4.0*aux1*q2)+(-4.0*q0*q1)+(4.0*q0*q2)+(-4.0*q1*q2)+(2.0)

Sample:[0, 1, 0, 0, 0] Energy:-2.0 Occurrence:62
Sample:[1, 1, 1, 1, 1] Energy:-2.0 Occurrence:23
Sample:[1, 0, 0, 1, 1] Energy:-2.0 Occurrence:175
Sample:[0, 0, 1, 1, 1] Energy:-2.0 Occurrence:56
Sample:[0, 0, 1, 1, 1] Energy:-2.0 Occurrence:1
Sample:[1, 0, 1, 1, 1] Energy:0.0 Occurrence:683

これで「３個の量子ビットから１個または３個を１にする」ができました。左側の３つがq0, q1, q2で、右側の２つが補助ビットです。条件式は、２つの補助ビットを巧みに使って２次より大きな相互作用が現れないようにしてあります。

係数の求め方

この魔法のような係数の求め方は、先程の記事を参考にさせていただきました。

以下はGoogle Colaboratoryでの実行を強く推奨します。ローカルの実行環境にpipしようとすると既存のパッケージ環境がなんか破壊されます（破壊されました）。

!pip install dwavebinarycsp
!pip install dwavebinarycsp[maxgap]

怒られるので、途中にある「RESTART RUNTIME」を押します。

import dwavebinarycsp

csp = dwavebinarycsp.ConstraintSatisfactionProblem(dwavebinarycsp.BINARY)
csp.add_constraint(lambda a, b, c: (a + b + c == 1) or (a + b + c == 3), ['q0', 'q1', 'q2'])
bqm = dwavebinarycsp.stitch(csp)

print(bqm)

BinaryQuadraticModel({'aux0': 0.0, 'aux1': 4.0, 'q0': 6.0, 'q1': -2.0, 'q2': 6.0}, {('aux0', 'aux1'): -4.0, ('aux0', 'q0'): -4.0, ('aux0', 'q1'): 4.0, ('aux0', 'q2'): -4.0, ('aux1', 'q0'): -4.0, ('aux1', 'q1'): 4.0, ('aux1', 'q2'): -4.0, ('q0', 'q1'): -4.0, ('q0', 'q2'): 4.0, ('q1', 'q2'): -4.0}, 2.0, Vartype.BINARY)

これが係数です。空気を読んで対応させてください。どんな計算を行っているかはまったく分かりません。。。

感謝の思いを込めて、スペシャルなコードを公開させていただきます。↑の「空気を読んで対応させてください」という面倒な作業を自動的にやってくれるコードです。

#Qビット名を取得
names = []
for name in bqm:
    names.append(name)
print(names)
#単体の係数
for name in names:
    print(name, bqm.linear[name])
#２体の係数
for i in range(len(names)):
    for j in range(i + 1, len(names)):
        try:
            print(names[i], names[j], bqm.adj[names[i]][names[j]])
        except:
            pass
#オフセット
print(bqm.offset)

#H=の形式で出力
command = 'H = 0 '
#単体の係数
for name in names:
    #ゼロでなければ式に追加
    if bqm.linear[name] != 0.0:
        command += '+({}*{})'.format(bqm.linear[name], name)
#２体の係数
for i in range(len(names)):
    for j in range(i + 1, len(names)):
        try:
            #ゼロでなければ式に追加
            if bqm.adj[names[i]][names[j]] != 0.0:
                command += '+({}*{}*{})'.format(bqm.adj[names[i]][names[j]], names[i], names[j])
        except:
            pass

#オフセット
command += '+({})'.format(bqm.offset)

print(command)

H = 0 +(4.0*aux1)+(6.0*q0)+(-2.0*q1)+(6.0*q2)+(-4.0*aux0*aux1)+(-4.0*aux0*q0)+(4.0*aux0*q1)+(-4.0*aux0*q2)+(-4.0*aux1*q0)+(4.0*aux1*q1)+(-4.0*aux1*q2)+(-4.0*q0*q1)+(4.0*q0*q2)+(-4.0*q1*q2)+(2.0)

結果をコピペすればそのまま条件式として使えます。（やったね）

３個の量子ビットから０個または２個を１にする

Colabの方で係数を求め、

csp.add_constraint(lambda a, b, c: (a + b + c == 0) or (a + b + c == 2), ['q0', 'q1', 'q2'])

H = 0 +(-4.0*aux0)+(10.0*q0)+(-6.0*q1)+(-6.0*q2)+(-4.0*aux0*aux1)+(-4.0*aux0*q0)+(4.0*aux0*q1)+(4.0*aux0*q2)+(-4.0*aux1*q0)+(4.0*aux1*q1)+(4.0*aux1*q2)+(-4.0*q0*q1)+(-4.0*q0*q2)+(4.0*q1*q2)+(8.0)

D-waveマシンに投げます。

#条件を記述する
aux0 = q3 #補助ビット
aux1 = q4 #補助ビット
H = (-4.0*aux0)+(10.0*q0)+(-6.0*q1)+(-6.0*q2)+(-4.0*aux0*aux1)+(-4.0*aux0*q0)+(4.0*aux0*q1)+(4.0*aux0*q2)+(-4.0*aux1*q0)+(4.0*aux1*q1)+(4.0*aux1*q2)+(-4.0*q0*q1)+(-4.0*q0*q2)+(4.0*q1*q2)+(8.0)

Sample:[1, 1, 0, 1, 1] Energy:-8.0 Occurrence:392
Sample:[0, 0, 0, 1, 1] Energy:-8.0 Occurrence:235
Sample:[1, 0, 1, 1, 1] Energy:-8.0 Occurrence:158
Sample:[0, 1, 1, 0, 0] Energy:-8.0 Occurrence:209
Sample:[1, 1, 1, 1, 0] Energy:-6.0 Occurrence:6

・・・できています、魔法です。

４個の量子ビットから１個または３個を１にする

同様に係数を求めました。

#４つの量子ビットを用意する
q0, q1, q2, q3, q4, q5 = Binary('q0'), Binary('q1'), Binary('q2'), Binary('q3'), Binary('q4'), Binary('q5')

#条件を記述する
aux0 = q4 #補助ビット
aux1 = q5 #補助ビット

H = (-6.0*q0)+(-6.0*q1)+(-2.0*q2)+(-2.0*q3)+(-8.0*aux1)+(4.0*q0*q1)+(4.0*q0*aux0)+(4.0*q0*aux1)+(4.0*q1*aux0)+(4.0*q1*aux1)+(4.0*q2*q3)+(-4.0*q2*aux0)+(4.0*q2*aux1)+(-4.0*q3*aux0)+(4.0*q3*aux1)+(10.0)

Sample:[0, 0, 1, 0, 1, 1] Energy:-10.0 Occurrence:57
Sample:[1, 1, 0, 1, 0, 0] Energy:-10.0 Occurrence:59
Sample:[1, 1, 0, 1, 0, 0] Energy:-10.0 Occurrence:48
Sample:[0, 0, 0, 1, 1, 1] Energy:-10.0 Occurrence:29
Sample:[0, 1, 1, 1, 1, 0] Energy:-10.0 Occurrence:24
Sample:[1, 1, 1, 0, 0, 0] Energy:-10.0 Occurrence:77
Sample:[0, 1, 0, 0, 0, 1] Energy:-10.0 Occurrence:102
Sample:[0, 1, 1, 1, 1, 0] Energy:-10.0 Occurrence:55
Sample:[1, 1, 1, 0, 0, 0] Energy:-10.0 Occurrence:137
Sample:[1, 0, 1, 1, 1, 0] Energy:-10.0 Occurrence:32
Sample:[1, 0, 1, 1, 1, 0] Energy:-10.0 Occurrence:53
Sample:[1, 0, 0, 0, 0, 1] Energy:-10.0 Occurrence:123
Sample:[0, 1, 0, 1, 1, 1] Energy:-8.0 Occurrence:17
Sample:[0, 1, 0, 1, 0, 1] Energy:-8.0 Occurrence:66
Sample:[0, 1, 1, 0, 1, 1] Energy:-8.0 Occurrence:46
Sample:[1, 0, 0, 1, 0, 1] Energy:-8.0 Occurrence:75

やたらに重複が多いですが、4C1 + 4C3 =８通りが出てきます。まじかよ！