29-2. 論理プログラミング言語「Prolog」（その２：ルールをPythonで再現してみた）

数理モデル / 論理

2021/11/29

概要
参考文献
家系図
性別の定義
ルール
再帰的なルール
おわりに

概要

PrologをPythonで再現しながら学んでいきます。内容もプログラムも前回の続きです。

参考文献

こちらの参考書の例題を踏襲しています。
Ivan Bratko(著)、安部憲広(翻訳)『Prologへの入門 (PrologとAI)』近代科学社

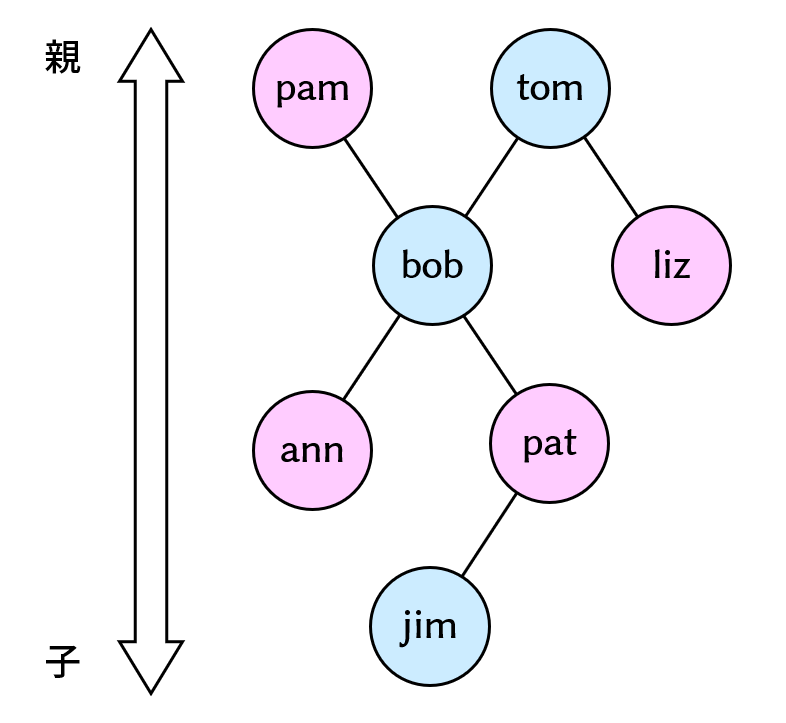
家系図

今回もこちらの家系図を参照します。

性別の定義

Prologで７人の性別を定義します。

female(pam).
male(tom).
male(bob).
female(liz).
female(pat).
female(ann).
male(jim).

確認してみます。

?-female(pam).   % pamは女性か？

yes

Pythonでも定義を追加します。

data = DEF(data, {'func':'female', 'arg1':'pam'})
data = DEF(data, {'func':'male', 'arg1':'tom'})
data = DEF(data, {'func':'male', 'arg1':'bob'})
data = DEF(data, {'func':'female', 'arg1':'liz'})
data = DEF(data, {'func':'female', 'arg1':'pat'})
data = DEF(data, {'func':'female', 'arg1':'ann'})
data = DEF(data, {'func':'male', 'arg1':'jim'})
print(data)

      func arg1 arg2
0   parent  pam  bob
1   parent  tom  bob
2   parent  tom  liz
3   parent  bob  ann
4   parent  bob  pat
5   parent  pat  jim
6   female  pam  NaN
7     male  tom  NaN
8     male  bob  NaN
9   female  liz  NaN
10  female  pat  NaN
11  female  ann  NaN
12    male  jim  NaN

arg2がNaNになっていますが問題ありません。

ルール

Prologではデータの「関係」を定義することができます。（ルールと呼びます）

offspring(Y, X) :- parent(X, Y)   % 『XがYの親』ならば『YはXの子』である

:- はネックまだはメダカとか呼ばれるようで、左側が結論部、右側が条件部です。「条件部を満たすX, Yがあるならばそれらは結論部も満たす」と定義することになります。ですので「『XがYの親』であるようなX, Yがあればそれらは『YはXの子』である」と一気に定義を加えるイメージです。※

※実際にはルールを解釈して複数の定義を加えているのではなく、単に一つのルールを書き込んだに過ぎません。質問した際にルールを参照してさらに深く定義を探しに行くような探索を行っているようです（次回言及します）。

条件部はカンマでAND処理もできます。

mother(X, Y) :- parent(X, Y), female(X).   % 『XがYの親』かつ『Xが女性』であれば『XはYの母親』

?- mother(X, bob).

X = pam

bobの母親については直接定義していませんが、ルールに従って論理的に答えてくれています。このようにして「父親」「grandparent（祖父母）」「sister（姉または妹）」等もルールできるかと思います。なお、条件部の変数を結論部ですべて使う必要はありません。

Pythonで「条件部の出力から定義を追加する関数」RULEDEF() を作りました。条件部を FIND() で行い、その出力を RULEDEF() に与えます。

#条件部の出力から定義を追加する関数
def RULEDEF(data, info, ret):
    #列名の積集合
    icols = list(set(list(info.values())) & set(list(ret.columns)))
    #順番に定義
    for i in range(len(ret)):
        tmp = {}
        #記号を復元（処理上の都合でkey,valを逆に）
        for key, val in info.items():
            tmp[key] = val #記号を復元
            #もし記号がretにあれば具体化
            if val in icols:
                tmp[key] = ret.loc[i, val]
        #定義
        data = DEF(data, tmp)
    return data

#offspring(Y, X) :- parent(X, Y)
ret = FIND({'func':'parent'}, {'arg1':'X', 'arg2':'Y'})
print(ret)
#ルールで定義
data = RULEDEF(data, {'func':'offspring', 'arg1':'Y', 'arg2':'X'}, ret)
print(data)

     X    Y
0  pam  bob
1  tom  bob
2  tom  liz
3  bob  ann
4  bob  pat
5  pat  jim
         func arg1 arg2
0      parent  pam  bob
1      parent  tom  bob
（中略）
11     female  ann  NaN
12       male  jim  NaN
13  offspring  bob  pam
14  offspring  bob  tom
15  offspring  liz  tom
16  offspring  ann  bob
17  offspring  pat  bob
18  offspring  jim  pat

ルールに従ってoffspringの定義が６個追加されていることが分かります。

同様に母親のルールも加えます。FIND() を AND() して RULEDEF() に与えます。

#mother(X, Y) :- parent(X, Y), female(X).
ret1 = FIND({'func':'parent'}, {'arg1':'X', 'arg2':'Y'})
ret2 = FIND({'func':'female'}, {'arg1':'X'})
ret3 = AND(ret1, ret2)
print(ret3)
#ルールで定義
data = RULEDEF(data, {'func':'mother', 'arg1':'X', 'arg2':'Y'}, ret3)
print(data)

     X    Y
0  pam  bob
1  pat  jim
         func arg1 arg2
0      parent  pam  bob
1      parent  tom  bob
（中略）
17  offspring  pat  bob
18  offspring  jim  pat
19     mother  pam  bob
20     mother  pat  jim

#?- mother(X, bob).
print(FIND({'func':'mother', 'arg2':'bob'}, {'arg1':'X'}))

     X
0  pam

Pythonではルールを解釈して複数の定義を追加しているため組合せ爆発になる可能性があります。Prolog内の処理とは異なりますのでご注意ください。

再帰的なルール

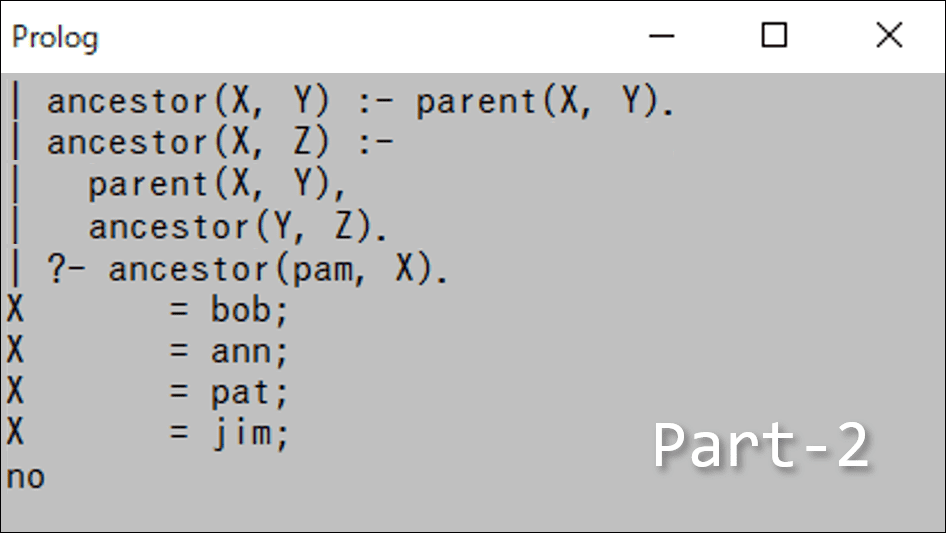
ここまでの内容でancestor（先祖）をルールしてみたいと思います。ancestorは親、祖父母、曽祖父母・・・のすべてを指すこととします。

単に

ancestor(X, Y) :- parent(X, Y).   % 親は先祖

とルールしても親の世代までしか届きません。ですからその初期条件の後に

ancestor(X, Z) :- parent(X, Y), ancestor(Y, Z).   % 先祖の親は先祖

と数珠つなぎなルールを書きます。数学的帰納法と言っても良いかもしれません。

ここで「pamを先祖に持つのは誰か？」と聞くと、

?- ancestor(pam, X).   % pamを先祖に持つのは誰か？

X = bob;
X = ann;
X = pat;
X = jim

４人答えてくれました。

これもPythonで再現します。再帰的な処理の再現が難しかったので、新しい定義が追加されなくなるまで無限回繰り返すことにしています。

#ancestor(X, Y) :- parent(X, Y).
ret = FIND({'func':'parent'}, {'arg1':'X', 'arg2':'Y'})
#ルールで定義
data = RULEDEF(data, {'func':'ancestor', 'arg1':'X', 'arg2':'Y'}, ret)

while 1:
    data_copy = deepcopy(data)
    
    #ancestor(X, Z) :- parent(X, Y), ancestor(Y, Z).
    ret1 = FIND({'func':'parent'}, {'arg1':'X', 'arg2':'Y'})
    ret2 = FIND({'func':'ancestor'}, {'arg1':'Y', 'arg2':'Z'})
    ret3 = AND(ret1, ret2)
    #ルールで定義
    data = RULEDEF(data, {'func':'ancestor', 'arg1':'X', 'arg2':'Z'}, ret3)
    
    #終了判定
    if data.equals(data_copy):
        break
print(data)

         func arg1 arg2
0      parent  pam  bob
1      parent  tom  bob
（中略）
19     mother  pam  bob
20     mother  pat  jim
21   ancestor  pam  bob
22   ancestor  tom  bob
23   ancestor  tom  liz
24   ancestor  bob  ann
25   ancestor  bob  pat
26   ancestor  pat  jim
27   ancestor  pam  ann
28   ancestor  pam  pat
29   ancestor  tom  ann
30   ancestor  tom  pat
31   ancestor  bob  jim
32   ancestor  pam  jim
33   ancestor  tom  jim

ancestorがたくさん定義されました。

#?- ancestor(pam, X).
print(FIND({'func':'ancestor', 'arg1':'pam'}, {'arg2':'X'}))

     X
0  bob
1  ann
2  pat
3  jim

質問にも適切に答えてくれました。

おわりに

今回は「ルール」を確認しました。次回は「探索」を行います。

29-3. 論理プログラミング言語「Prolog」（その３：グラコロバーガーの合成で学ぶ探索の基本形）

概要前回まではPrologをPythonで再現しながら学んでいましたが、早くもPythonでの再現を諦めました。今回はPrologで探索を学びます。参考文献...