やること
どうしてもオートエンコーダで画像を2次元まで次元圧縮したい。今日は最終手段を使って、ケーキ画像の次元圧縮をしてみます。
使うもの
Google Colaboratoryが利用可能です。


最終手段とは
オートエンコーダは「入力と同じ出力を出す変換器」ですが、出力を10種のケーキラベルとし、クラス分類問題にします。すなわち、入力は画像、出力は10次元のラベルです。このようにすると、途中の2次元の部分は、通常は「元の画像を復元するのに十分な情報」を保持していることが期待されますが、ここでは「10クラスに正しく分類するのに十分な情報」を保持することに注意します。

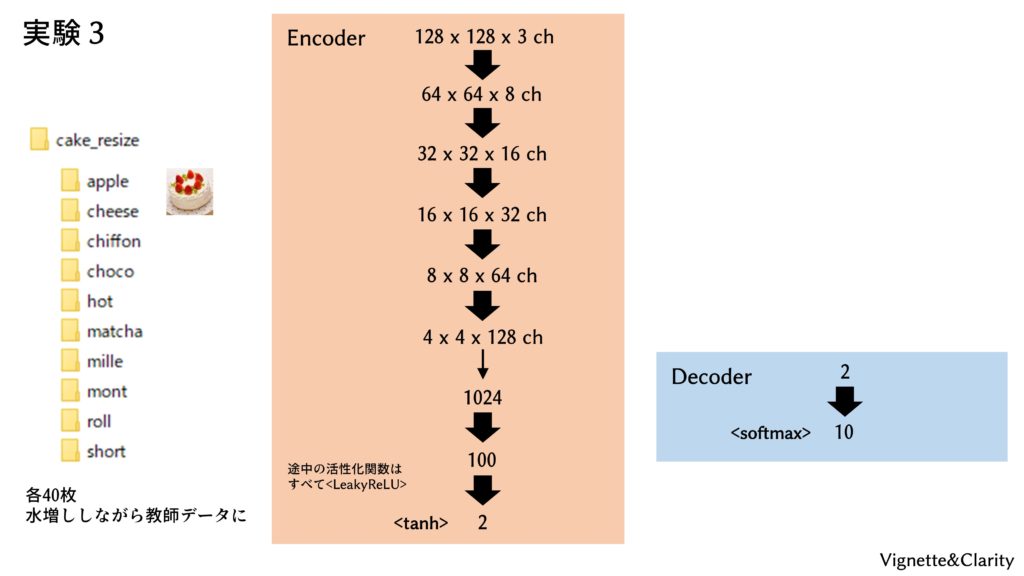
ニューラルネットモデル
1-3, 1-4で用意した、10種のケーキの画像(計400枚)を用いますが、ここでは「apple」「cheese」といったラベルも学習に用いるので、もはや教師なし学習とは言えません。オートエンコーダでもないし、教師なし学習でもない。いったい何をやっているんでしょうか。
プログラムを実行する
配布された「autoencoder_3.py」を実行すると、「cake_AE3_para/」フォルダが生成され、50エポックごとに重みとバイアスが保存されます。オートエンコーダの性能確認として、40枚×10クラスのケーキを入力したときの2次元の変数(潜在変数)を、クラスごとに色違いでプロットしています。0エポック時はまったく学習されていないので、潜在変数は0付近に集中しています。潜在変数がこんなに近いと、分類もうまくできないでしょう。学習が進むと、潜在変数のプロットは天の川のように広がり、見ていてとてもキレイです(疲労感)。

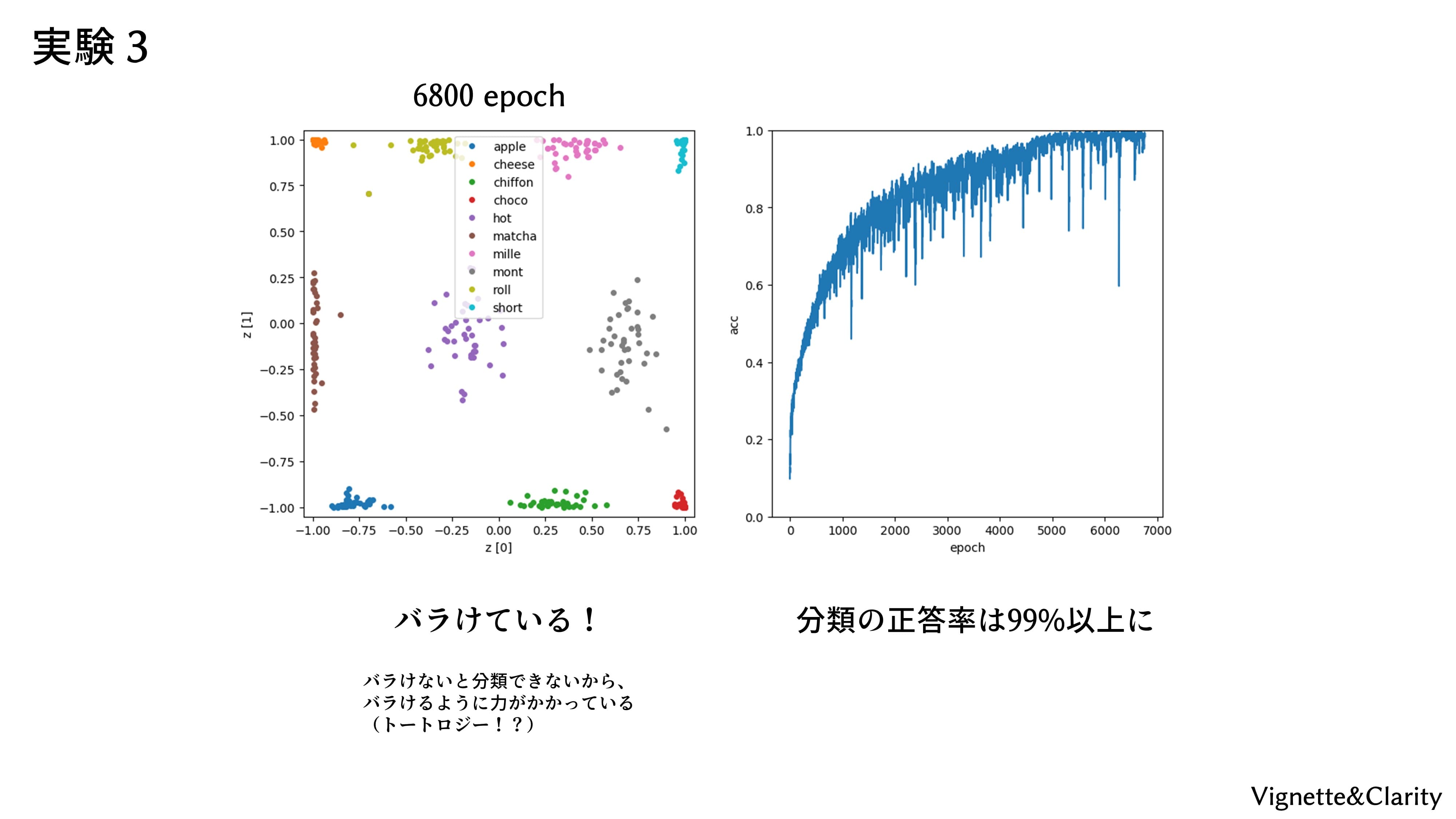
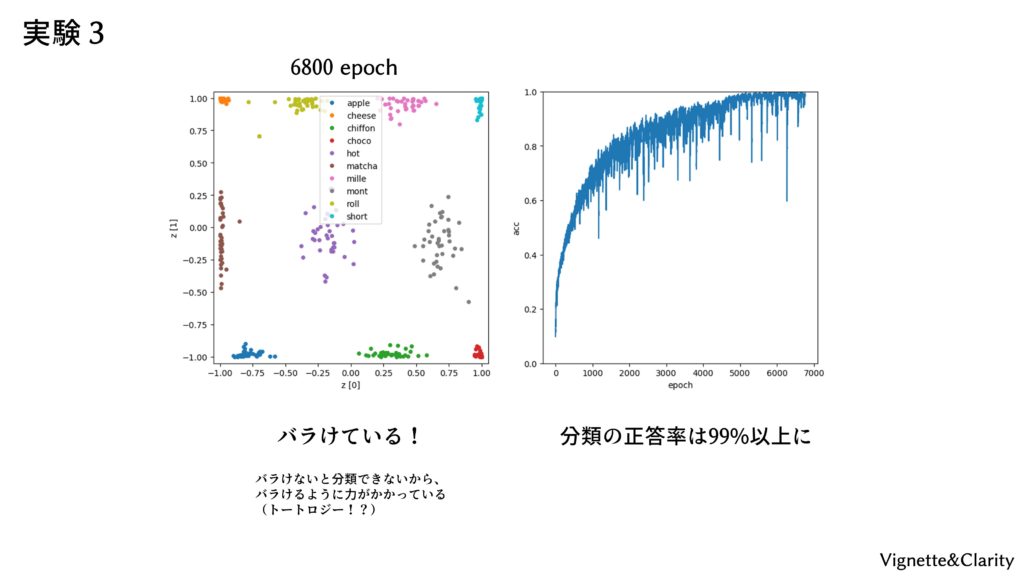
結果
6800エポックで正答率99%くらいになりました。潜在変数は見事に10クラスタにバラけています。バラけないと分類はできないので、バラけるように力がかかっています。最終手段を使いましたが、リベンジ達成ということにしてください(諦め)。
Q&Aコーナー
Q. 圧縮後の2次元(潜在変数)って、それぞれ何を意味するの?
A. 分かりませんので、人間が解釈を与える必要があります。例えば、「茶色っぽさ」と「クリーム層があるか」といった具合です。
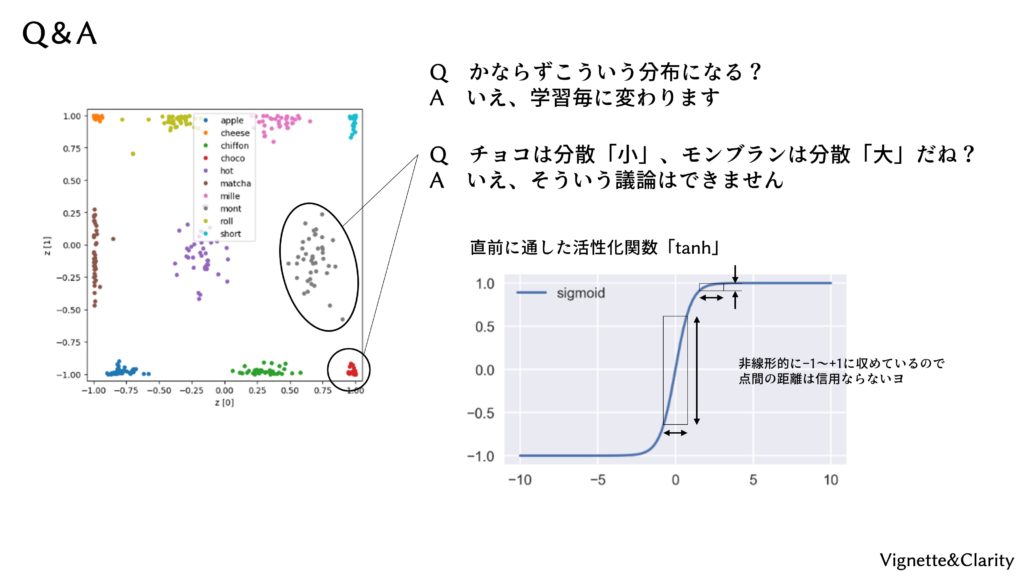
Q. 必ずこういう分布になる?
A. 学習ごとにクラスタの位置が変わります。
Q. 例えば、チョコケーキは分散が小さく、モンブランは分散が大きいと言えますか?
A. いえ、潜在空間内での部分によって距離感が異なるので、そういった距離や分散の議論はできません。