概要
選挙ということで、「日本の年齢別人口比率に基づいて100人の代議員を割り当てるなら20代は何人になるか?」という問い合わせがありました(もちろん嘘)。
単純計算すると、20代/全体=1262/12512[万人]=10.1%だから10人でしょう?と思いますが、このように割り当てていくと合計100人にならない場合があります。円グラフでよく見る「※四捨五入の関係で合計が100%にならない場合があります」と同じ問題です。
ここでは人口比率に基づいた正確な代議員の割り当てについて考えてみます。
参考文献
いつもお世話になっている総務省統計局の人口推計です。
https://www.stat.go.jp/data/jinsui/pdf/202110.pdf
人口比率のプロット
ここでは0~4歳、5~9歳、・・・、95~100歳の20クラスを考えます。実際の人口推計から20クラスのヒストグラムを表示します。
import numpy as np
from copy import deepcopy
import matplotlib.pyplot as plt
#人口ビン、0歳から5歳刻みで100歳まで(20クラス)
pop_bin = np.array([450,497,532,555,631,631,642,725,809,966,919,778,737,787,970,675,559,389,192,59])
print(pop_bin)
#代議員の生成数
num = 100
#比率ヒストグラムの確認
def show(pop_rate=np.zeros(20), delegate_rate=np.zeros(20)):
plt.bar(np.arange(20)-0.2, delegate_rate, 0.4, fill=None, hatch='///', label='delegate_rate')
plt.bar(np.arange(20)+0.2, pop_rate, 0.4, color='gray', label='pop_rate')
plt.xticks(np.arange(20), rotation=0) #目盛りを省略しないための設定
plt.legend()
plt.xlabel('age class'); plt.ylabel('rate')
plt.show()
#人口比率
pop_rate = pop_bin / np.sum(pop_bin)
#確認
show(pop_rate=pop_rate)[450 497 532 555 631 631 642 725 809 966 919 778 737 787 970 675 559 389
192 59]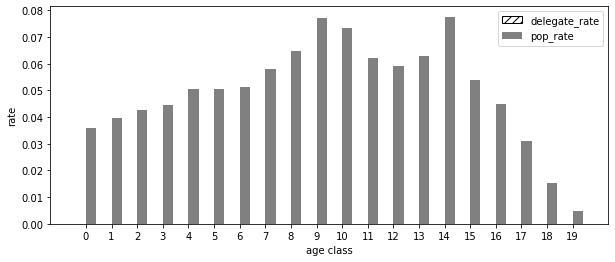
見事な「つぼ型」の分布になっています。ろくろで作って「2020年モデル 20万円」「2045年モデル 45万円」とか売っても面白そうですね!
代議員の割り当て
次に100人の代議員を振り分けていきます。cumsumは累積和のことで、ここでは区切り箇所のように使います。100人に先頭から0.00, 0.01, 0.02, …, 0.99と番号を付け、自分がいる区切りに応じてクラス番号が割り振られます。
#人口比率の累積和(最大1)
cumsum = np.cumsum(pop_rate)
print(cumsum)
#代議員生成
delegate = [np.sum(i/num >= cumsum) for i in range(num)]
print(delegate)
#代議員ビンと比率
delegate_bin = np.bincount(delegate, minlength=20)
print(delegate_bin)
delegate_rate = delegate_bin / np.sum(delegate_bin)
print(delegate_rate)
#確認
show(pop_rate=pop_rate, delegate_rate=delegate_rate)[0.03599136 0.07574182 0.11829161 0.16268096 0.21314884 0.26361673
0.31496441 0.37295049 0.43765496 0.51491642 0.58841878 0.65064385
0.7095897 0.77253459 0.85011597 0.90410302 0.94881229 0.97992482
0.99528113 1. ]
[0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 6, 6, 6, 6, 6, 7, 7, 7, 7, 7, 7, 8, 8, 8, 8, 8, 8, 9, 9, 9, 9, 9, 9, 9, 9, 10, 10, 10, 10, 10, 10, 10, 11, 11, 11, 11, 11, 11, 11, 12, 12, 12, 12, 12, 13, 13, 13, 13, 13, 13, 13, 14, 14, 14, 14, 14, 14, 14, 14, 15, 15, 15, 15, 15, 16, 16, 16, 16, 17, 17, 17, 18, 18]
[4 4 4 5 5 5 5 6 6 8 7 7 5 7 8 5 4 3 2 0]
[0.04 0.04 0.04 0.05 0.05 0.05 0.05 0.06 0.06 0.08 0.07 0.07 0.05 0.07
0.08 0.05 0.04 0.03 0.02 0. ]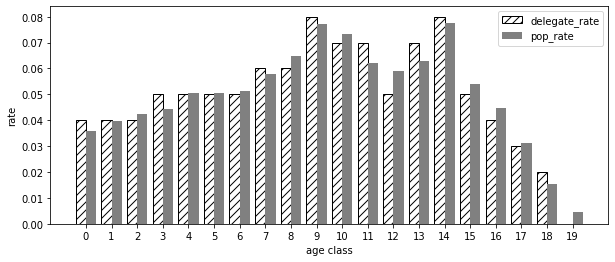
とりあえず単純な割り当てができました。100人ですから比率は0.01単位しか取り得ません。
問題点
この方法では手前から順に割り当てることによるしわ寄せが最終クラス影響したり、区切りの都合で妙に多い/少ないクラスが出現したりします。実際によく見てみるとクラス11が多い、クラス12が少ない、という状況になっています。
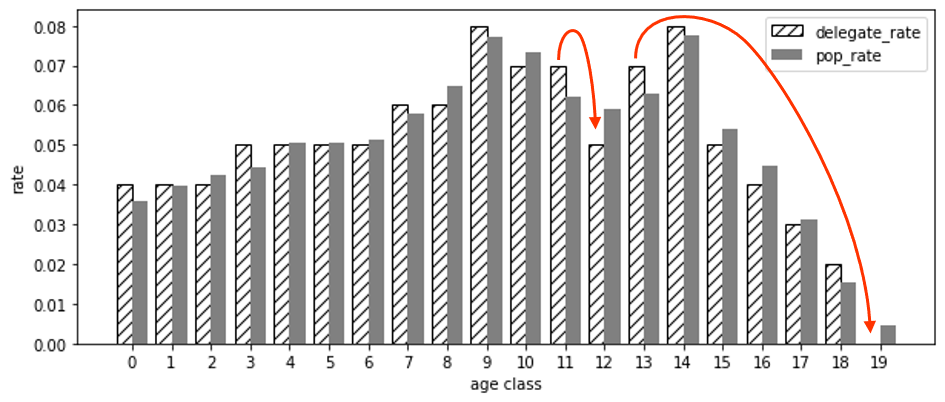
そこで、過剰なクラスから不足のクラスに移籍してもらう作業を、改善しなくなるまで繰り返し行ってみます。
調整
このような繰り返し調整はよく使うのでテンプレートとして持っておくと便利です。
#調整
for i in range(999):
#コピーしておく
delegate_save = deepcopy(delegate)
#代議員比率
delegate_bin = np.bincount(delegate, minlength=20)
delegate_rate = delegate_bin / np.sum(delegate_bin)
#処理前の最大ずれ
diff1 = np.max((delegate_rate - pop_rate)**2)
#一番過剰なクラス
index1 = np.argmax(delegate_rate - pop_rate)
#一番足りないクラス
index2 = np.argmin(delegate_rate - pop_rate)
#過剰なクラスから不足のクラスへ一人移動
print('{} -> {}'.format(index1, index2))
delegate[list(delegate).index(index1)] = index2
#処理後の代議員比率
delegate_bin = np.bincount(delegate, minlength=20)
delegate_rate = delegate_bin / np.sum(delegate_bin)
#処理後の最大ずれ
diff2 = np.max((delegate_rate - pop_rate)**2)
#改善しなかったらコピーを復元して終了
if diff2 >= diff1:
delegate = deepcopy(delegate_save)
print('not improved')
break
print(delegate)
#代議員ビンと比率
delegate_bin = np.bincount(delegate, minlength=20)
delegate_rate = delegate_bin / np.sum(delegate_bin)
#確認
show(pop_rate=pop_rate, delegate_rate=delegate_rate)11 -> 12
13 -> 19
3 -> 16
16 -> 8
not improved
[0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 2, 2, 16, 3, 3, 3, 3, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 6, 6, 6, 6, 6, 7, 7, 7, 7, 7, 7, 8, 8, 8, 8, 8, 8, 9, 9, 9, 9, 9, 9, 9, 9, 10, 10, 10, 10, 10, 10, 10, 12, 11, 11, 11, 11, 11, 11, 12, 12, 12, 12, 12, 19, 13, 13, 13, 13, 13, 13, 14, 14, 14, 14, 14, 14, 14, 14, 15, 15, 15, 15, 15, 16, 16, 16, 16, 17, 17, 17, 18, 18]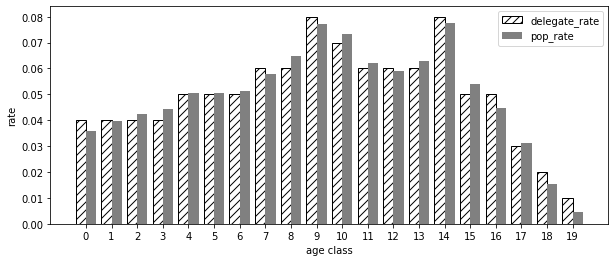
出力が意味するところは、3回目までの移籍が有効で4回目の移籍では改善しなかったということです。このように「”もっともズレが大きい箇所”を最小にする」方針をミニマックス法と呼ぶことがあります。
おわりに
年金は受給開始を遅くすると増額になるようですが、それが通用しなくなってきたら壺を売ってみてはいかがでしょうか。この壷(100万円(税込120万円))を買うと年金が増額になります(+5万円/年)!

