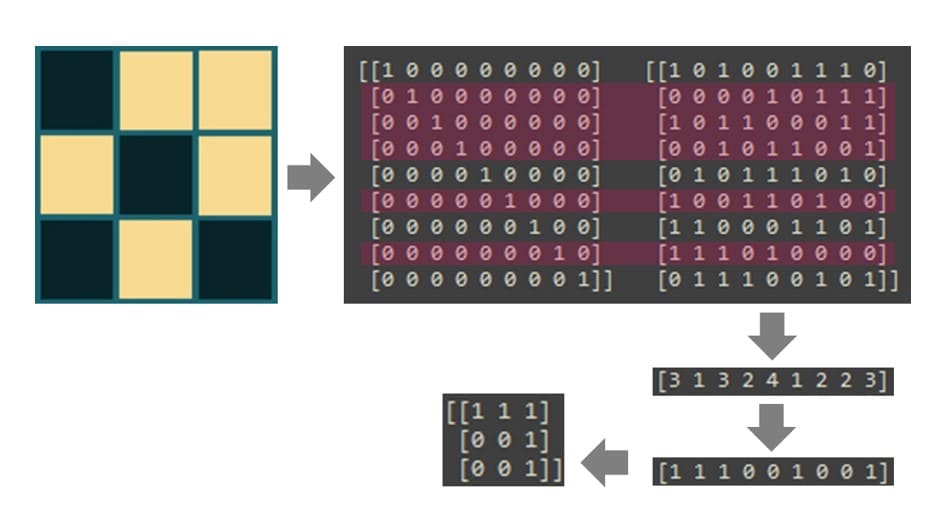
10/15(火)-10/19(土)　岐阜県（南濃温泉「水晶の湯」）で自動運転車の実証実験を行います☆彡

5-20. ライツアウトを理論的に解く（Pythonコード付）

やること

以前、ライツアウトというパズルを遺伝的アルゴリズム（GA）で解きました。

20-3. 遺伝的アルゴリズム（vcopt）でライツアウトを解く
やることライツアウト（lights out）というパズルがあります。ライトを消せ！的な意味です。例題１マスをクリックすると、そのマスを含む十字型の５マスがひっ...
vigne-cla.com
2020/01/29

GAでは、５✕５サイズを解くのに十数秒かかっていました。今回はもっと早く確実に解ける理論解法を試してみたいと思います。

ルールのおさらい

前回と同じ例題です。

マスをクリックすると、そのマスを含む十字型の５マスがひっくり返ります。マスをすべて消灯させればクリアです。解答は一意に定まりませんが、最少手数の答えがこちらです。

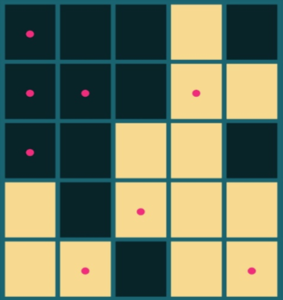
同じマスを２回以上クリックすることには意味がないため、各マスとも「１回クリックする」か「クリックしない」の２択しかありません。

理論解法

いきなりですが、こちらの記事に全て書かれていました。takaken様に感謝申し上げます。

301 Moved Permanently
www.ic-net.or.jp

また、線形代数がわかる方はこちらもご参照ください。

Lights Outを線形代数で解く - Qiita
はじめにカジュアルにパズルを楽しめるスマホアプリの1つにLightsOutがあります。LightsOutはシンプルなゲームながら面白い数学を使った話が隠れています。この記事では、LightsO…
qiita.com

実行環境

WinPython3.6をおすすめしています。

WinPython - Browse /WinPython_3.6/3.6.7.0 at SourceForge.net
Portable Scientific Python 2/3 32/64bit Distribution for Windows
sourceforge.net

Google Colaboratoryが利用可能です。

Google Colab
colab.research.google.com

考え方（前半）

ここからはtakaken様の記事の解き方をPythonで実装するだけですので、オリジナリティは低めです。

前半の処理はパズルのサイズだけに依存し、具体的な問題盤面とは無関係であることに注意してください。３✕３サイズでは次のようなことをします。

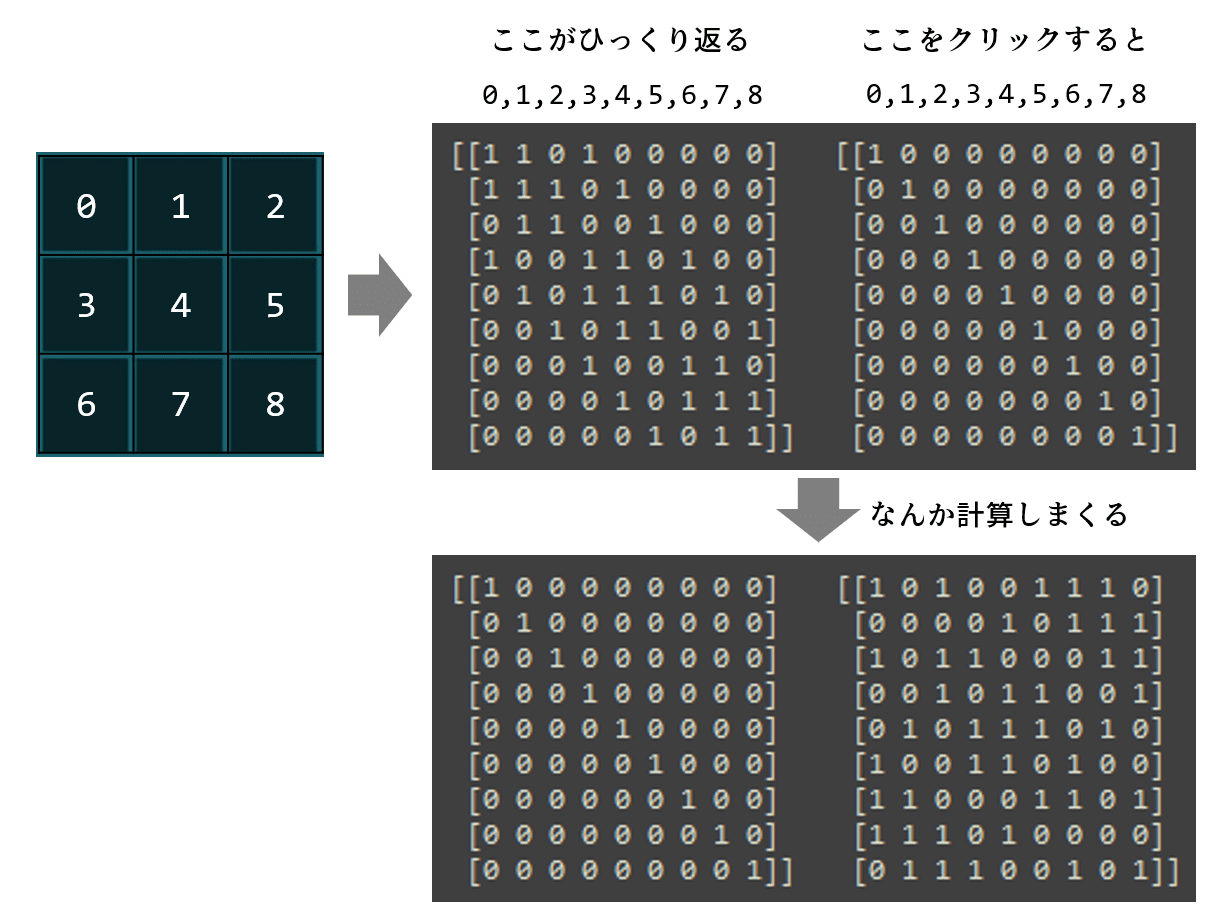
計算前は右辺が単位行列（１が斜めに並んでいる）の状態です。1行目は、「0番をクリックすると0, 1, 3番がひっくり返る」ことを意味しています。これはマスを丁寧に見れば分かることですね。

これらをうまいこと計算して左辺を単位行列に変換します。「0番のマスだけをひっくり返すには0, 2, 5, 6, 7番をクリックすれば良い」という法則に変換してやるということです。実際の問題において0番が点灯していれば、0, 2, 5, 6, 7番をクリックすることで他のマスに影響を与えることなく0番を消灯できるのです。

考え方（後半）

後半は実際の問題盤面を用います。点灯マスに該当する行を抽出し、各マスのクリック回数を集計します。同じマスを２回クリックすることは０回と同じであるため、2で割った余りを求めます。これが最終的な各マスのクリック回数です。

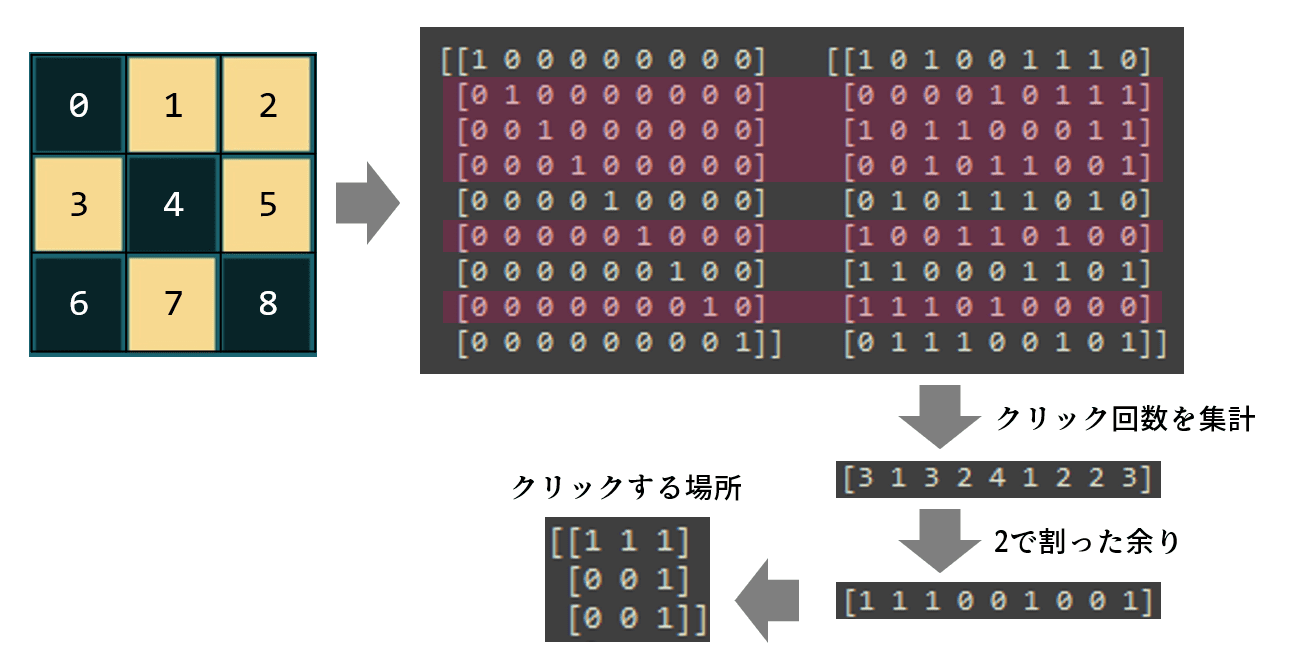
興味深いことに、同じサイズの盤面であれば、問題が変わっても前半の結果は使い回せます。高速で解答が得られるわけです。

コード（前半）

５✕５サイズで実装してみます。前半は具体的な問題は必要とせず、５✕５という情報だけで進めます。

準備

import numpy as np
from scipy import signal

#畳み込みフィルタ
g = np.array([[0, 1, 0],
              [1, 1, 1],
              [0, 1, 0]])

#サイズ
h, w = 5, 5

行列の用意

#計算マトリックス用意
mat = np.zeros((h*w, h*w, 2), int)

#左辺
for i in range(h):
    for j in range(w):
        #4近傍のマス
        mask = np.zeros((h, w), int)
        mask[i, j] = 1
        mask = signal.convolve2d(mask, g, mode='same', boundary='fill', fillvalue=0) // 1
        #格納
        mat[i*h + j, :, 0] = mask.flatten()

#右辺（単位行列）
mat[:, :, 1] = np.diag(np.ones(h*w, int))

print(mat[:, :, 0])
print(mat[:, :, 1])
[[1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [1 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 1 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 1 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 1 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [1 0 0 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 1 0 0 0 1 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 1 0 0 0 1 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 1 0 0 0 1 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 1 0 0 0 1 1 1 0 0 0 1 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 1 0 0 0 1 1 1 0 0 0 1 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 1 0 0 0 1 1 1 0 0 0 1 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 1 0 0 0 1 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 1 0 0 0 1 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 1 0 0 0 1 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 1 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 1 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 1]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1]]
[[1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1]]

計算

#計算
for i in range(h*w):
    print('i = {}'.format(i))
    
    #ターゲット列の1の場所
    index = np.where(mat[:, i, 0] == 1)[0]
    #print(index)
    
    #1が自分の後ろになければ終わり
    if i > index[-1]:
        print('end')
        break
    
    #1の場所のうち、自分より後ろの一つ（自分でもいい）
    target_index = index[np.where(index >= i)[0][0]]
    #print(target_index)
    
    #自分の行とその行を交換（ターゲットポジションに1をもってくる）
    mat[i, :], mat[target_index, :] = mat[target_index, :], np.copy(mat[i, :])
    
    #ターゲット列の1の場所
    index = np.where(mat[:, i, 0] == 1)[0]
    #print(index)
    
    #自分を除く
    index = index[index != i]
    #print(index)
    
    #自分以外に対してxor（両辺同時に処理）
    for k in index:
        mat[k, :, :] = mat[i, :, :] != mat[k, :, :]
    
print(mat[:, :, 0])
print(mat[:, :, 1])
i = 0
i = 1
i = 2
i = 3
i = 4
i = 5
i = 6
i = 7
i = 8
i = 9
i = 10
i = 11
i = 12
i = 13
i = 14
i = 15
i = 16
i = 17
i = 18
i = 19
i = 20
i = 21
i = 22
i = 23
end
[[1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1]
 [0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0]
 [0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1]
 [0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0]
 [0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1]
 [0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1]
 [0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1]
 [0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1]
 [0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0]
 [0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 1]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]]
[[0 1 1 1 0 0 0 1 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 0 0]
 [1 1 0 1 1 0 1 0 0 0 0 0 1 1 1 0 0 0 1 0 0 0 0 0 0]
 [1 0 1 1 1 1 0 1 1 0 0 0 1 1 0 1 1 1 1 1 0 1 0 0 0]
 [1 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 1 0 0]
 [0 1 1 0 1 1 0 0 0 0 1 0 1 0 1 0 0 1 0 1 1 1 0 0 0]
 [0 0 1 0 1 0 1 1 0 1 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0]
 [0 1 0 1 0 1 1 0 1 1 0 0 0 1 0 1 1 1 0 0 0 1 0 0 0]
 [1 0 1 0 0 1 0 1 1 0 0 0 0 0 1 1 0 1 0 1 1 0 1 0 0]
 [0 0 1 0 0 0 1 1 1 0 1 0 0 1 1 1 0 0 1 0 0 1 1 0 0]
 [1 0 0 0 0 1 1 0 0 0 1 0 1 0 1 0 1 1 0 1 0 0 1 0 0]
 [0 0 0 0 1 0 0 0 1 1 0 0 1 0 1 1 1 1 1 0 0 1 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 1 0 0]
 [0 1 1 0 1 1 0 0 0 1 1 0 1 1 0 0 0 1 0 0 1 1 0 0 0]
 [1 1 1 0 0 0 1 0 1 0 0 0 1 1 1 0 0 0 1 0 0 0 0 0 0]
 [1 1 0 0 1 0 0 1 1 1 1 0 0 1 1 1 1 0 1 0 1 0 0 0 0]
 [0 0 1 0 0 0 1 1 1 0 1 0 0 0 1 1 0 1 0 1 1 0 1 0 0]
 [0 0 1 1 0 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 0 0 1 0 0]
 [0 0 1 0 1 0 1 1 0 1 1 0 1 0 0 1 1 0 1 1 1 0 0 0 0]
 [0 1 1 0 0 1 0 0 1 0 1 0 0 1 1 0 1 1 1 0 0 0 1 0 0]
 [1 0 1 0 1 1 0 1 0 1 0 0 0 0 0 1 0 1 0 1 1 0 1 0 0]
 [0 0 0 1 1 0 0 1 0 0 0 1 1 0 1 1 0 1 0 1 1 1 0 0 0]
 [0 0 1 1 1 0 1 0 1 0 1 1 1 0 0 0 0 0 0 0 1 1 1 0 0]
 [0 0 0 1 0 0 0 1 1 1 0 1 0 0 0 1 1 0 1 1 0 1 0 0 0]
 [0 1 1 1 0 1 0 1 0 1 1 1 0 1 1 1 0 1 0 1 0 1 1 1 0]
 [1 0 1 0 1 1 0 1 0 1 0 0 0 0 0 1 0 1 0 1 1 0 1 0 1]]

できました。５✕５サイズにおいて最後の２マスが一意に定まらないことに関してはtakaken様の記事を参照。ここでは無視して進めます。

コード（後半）

問題の読み込み

#問題
lights = ['---#-',
          '---##',
          '--##-',
          '#-###',
          '##-##']

#問題を0,1に変換
f = np.array([list(l) for l in lights])
f = np.where(f=='#', 1, 0)
print(f)
[[0 0 0 1 0]
 [0 0 0 1 1]
 [0 0 1 1 0]
 [1 0 1 1 1]
 [1 1 0 1 1]]

点灯マスが関わる行を抽出してクリック回数を集計。解答を得る。

#ライトが付いているマスのマスク
mask = f.flatten().astype(bool)
print(mask)

#の行だけ見ればいいので右辺を抽出
ans = mat[mask, :, 1]
print(ans)

#マスのクリックする回数を集計、2で割った余り
ans = np.sum(ans, axis=0) % 2
print(ans)

#クリックする場所
ans = ans.reshape(h, w) 
print(ans)
[False False False  True False False False False  True  True False False
  True  True False  True False  True  True  True  True  True False  True
  True]
[[1 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 1 0 0]
 [0 0 1 0 0 0 1 1 1 0 1 0 0 1 1 1 0 0 1 0 0 1 1 0 0]
 [1 0 0 0 0 1 1 0 0 0 1 0 1 0 1 0 1 1 0 1 0 0 1 0 0]
 [0 1 1 0 1 1 0 0 0 1 1 0 1 1 0 0 0 1 0 0 1 1 0 0 0]
 [1 1 1 0 0 0 1 0 1 0 0 0 1 1 1 0 0 0 1 0 0 0 0 0 0]
 [0 0 1 0 0 0 1 1 1 0 1 0 0 0 1 1 0 1 0 1 1 0 1 0 0]
 [0 0 1 0 1 0 1 1 0 1 1 0 1 0 0 1 1 0 1 1 1 0 0 0 0]
 [0 1 1 0 0 1 0 0 1 0 1 0 0 1 1 0 1 1 1 0 0 0 1 0 0]
 [1 0 1 0 1 1 0 1 0 1 0 0 0 0 0 1 0 1 0 1 1 0 1 0 0]
 [0 0 0 1 1 0 0 1 0 0 0 1 1 0 1 1 0 1 0 1 1 1 0 0 0]
 [0 0 1 1 1 0 1 0 1 0 1 1 1 0 0 0 0 0 0 0 1 1 1 0 0]
 [0 1 1 1 0 1 0 1 0 1 1 1 0 1 1 1 0 1 0 1 0 1 1 1 0]
 [1 0 1 0 1 1 0 1 0 1 0 0 0 0 0 1 0 1 0 1 1 0 1 0 1]]
[1 1 1 1 0 0 1 1 1 1 0 1 0 1 1 1 0 0 0 1 0 0 1 1 1]
[[1 1 1 1 0]
 [0 1 1 1 1]
 [0 1 0 1 1]
 [1 0 0 0 1]
 [0 0 1 1 1]]

プレイする関数を用意。解答に従ってプレイ。

#答えにしたがってプレイする関数
def play(lights, ans):
    #ひっくり返る回数
    flip_num = signal.convolve2d(ans, g, mode='same', boundary='fill', fillvalue=0)
    
    #盤面と合計、偶数マスは０、奇数マスは１
    result = (lights + flip_num) % 2
    
    return result

#解答でプレイ
after = play(f, ans)
print(after)
[[0 0 0 0 0]
 [0 0 0 0 0]
 [0 0 0 0 0]
 [0 0 0 0 0]
 [0 0 0 0 0]]

見事に全部消灯しました！

おまけ

takaken様の記事によれば５✕５サイズでは解が４種類あるとのことで、他の解も出してみます。

#解答のバリエーション1
var1 = np.array([[0,1,1,1,0],
                 [1,0,1,0,1],
                 [1,1,0,1,1],
                 [1,0,1,0,1],
                 [0,1,1,1,0]], int)
ans1 = (ans != var1).astype(int)
print(ans1)
#プレイ
after = play(f, ans1)
print(after)

#解答のバリエーション2
var2 = np.array([[1,0,1,0,1],
                 [1,0,1,0,1],
                 [0,0,0,0,0],
                 [1,0,1,0,1],
                 [1,0,1,0,1]], int)
ans2 = (ans != var2).astype(int)
print(ans2)
#プレイ
after = play(f, ans2)
print(after)

#解答のバリエーション3
var3 = np.array([[1,1,0,1,1],
                 [0,0,0,0,0],
                 [1,1,0,1,1],
                 [0,0,0,0,0],
                 [1,1,0,1,1]], int)
ans3 = (ans != var3).astype(int)
print(ans3)
#プレイ
after = play(f, ans3)
print(after)
[[1 0 0 0 0]
 [1 1 0 1 0]
 [1 0 0 0 0]
 [0 0 1 0 0]
 [0 1 0 0 1]]
[[0 0 0 0 0]
 [0 0 0 0 0]
 [0 0 0 0 0]
 [0 0 0 0 0]
 [0 0 0 0 0]]
[[0 1 0 1 1]
 [1 1 0 1 0]
 [0 1 0 1 1]
 [0 0 1 0 0]
 [1 0 0 1 0]]
[[0 0 0 0 0]
 [0 0 0 0 0]
 [0 0 0 0 0]
 [0 0 0 0 0]
 [0 0 0 0 0]]
[[0 0 1 0 1]
 [0 1 1 1 1]
 [1 0 0 0 0]
 [1 0 0 0 1]
 [1 1 1 0 0]]
[[0 0 0 0 0]
 [0 0 0 0 0]
 [0 0 0 0 0]
 [0 0 0 0 0]
 [0 0 0 0 0]]

他の３つの解も機械的に得られました。これら４つの解を比較することで最小手数の解が分かるということです。確かに、冒頭に示した最小手数の解がありますね。素晴らしい。

さいごに

素晴らしかったです。数学が分かるとパズルがこんなにも楽しくなるのですね。人によっては、つまらなくなったと感じるかもしれません。これからも楽しく数学していきましょう。

タイトルとURLをコピーしました