5-23. Excelやスプレッドシートでシード付き一様乱数を生成

やること

ExcelやGoogleスプレッドシートには一様乱数を生成する RAND() 関数が用意されていますが、シード値を指定できません。どこかのセルを変更したりファイルを開き直したりするとサイコロが振り直しになって値が変わります。

シード値を指定できないと困る場面というのが、イベントの参加申し込みを受けて抽選をするときです。

科学実験では再現性のために必ずシード値を指定・記録しておくものですが、たかだか30人の申込者を抽選するためにシード値を指定する必要は、実際のところ全くありません。RAND() で生成した一様乱数を「数値として貼り付け」で魚拓しておいて、それを使って抽選すればいいだけです。

しかし、私はこの方法が好きではありません。というのは抽選結果に対する責任の所在を明確にしたいからです。いわば「こいつのせいであなたは落選しました」というハッキリした悪役を擁立しておきたいのです。

精一杯の菩薩の表情で RAND() サイコロを振ったとしても、心の中で「この人はなぜ落選したのだろう？」という問答が発生するわけです。「コンピュータが決めました」と言って、彼は納得できるでしょうか？また、1分前に抽選していたら結果が変わったかもしれません。他のスタッフが抽選しても運命は変わったかもしれません。もう一人申し込みがあれば、あるいはキャンセルが出ていれば一行ズレていたのでは…？とも思えるわけです。

そうやって「なぜ私は落選したのですか？」の問いから逃げるように心の扉を閉ざすことが落選者への誠意になるのでしょうか？

ですから、要するに私は「シード値」を唯一の責任者に掲げて、恨むならこいつを恨んでください、という無責任なカタルシスを得たいのです。

ということで、長々話しましたが、「申込者に固有のID」と「シード値」だけに紐づく独自の疑似乱数（一様乱数）を、ExcelとGoogleスプレッドシートで作ってみます。

参考文献

線形合同法を使います。

線形合同法 - Wikipedia

ja.wikipedia.org

線形合同法の周期について。

線形合同法 - Algoful

線形合同法は最も古く、また最もよく知られ...

algoful.com

完成形

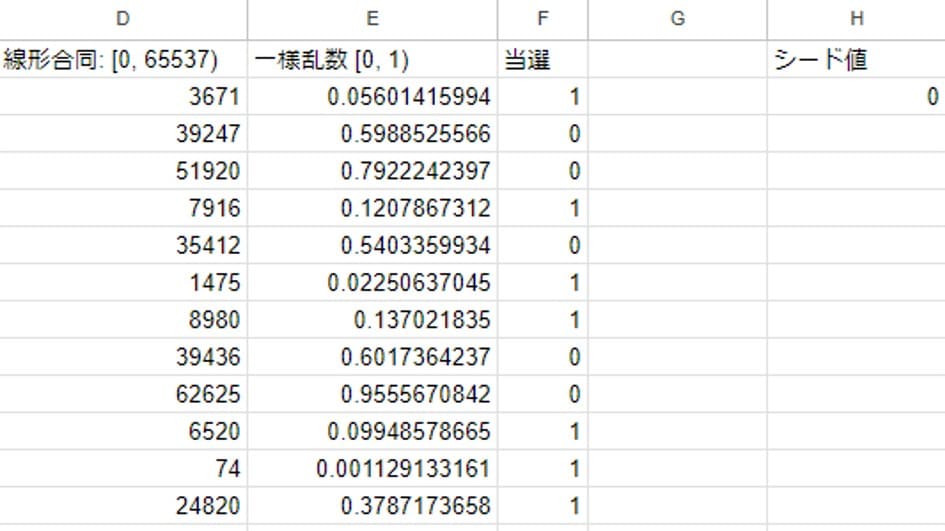
完成形がこちら。A列の「申し込みID」と右側にある「シード値」を元にしてE列に一様乱数を生成します。

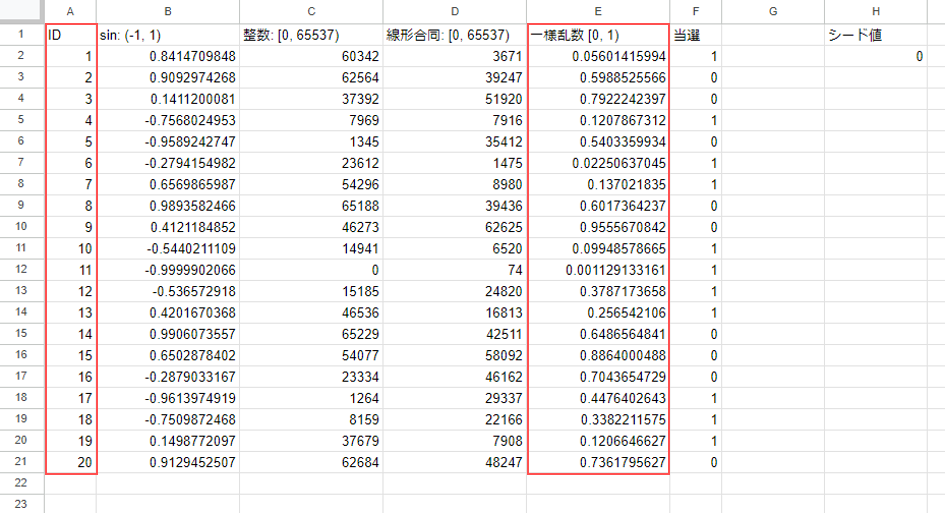
この方法では、申し込みのキャンセルがあった場合に行を削除しても他に影響がありません。IDとシード値が変わらなければ結果も保たれます。

手順

B列

まず、A列をsin関数に入れたものをB列とします。範囲は (-1, 1) です。

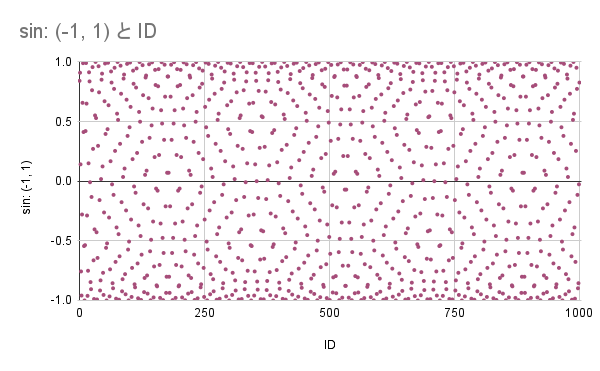
=sin(A2 + 32768*H$2)

この処理の目的は、「範囲不明の整数」を「一定範囲の重複しない数」に変換することです。sinの中には無理数を入れない限り重複した値が出ません（あれ、そうですよね？）。このとき「32768×シード値」だけロールしておくことで、シード値を1でもずらすと予測不能レベルでごっそり変わります。次の図はID1～1000まで1000人のB列をプロットしたものです。現在は規則性が見えています（ただし重複はない）。

C列

次に、B列を0～65536の整数に引き伸ばします。

=rounddown(32768.5*B2 + 32768.5, 0)

なぜ0～65536の整数にしたかというと、次のステップ用いる線形合同法が0～65536の整数を元に0～65536の整数を生成する処理だからです。それに合わせました。1000人のプロットはほとんど同じ見た目ですが、整数に丸めたことで低確率で重複が発生しているかもしれません（上端と下端の密度高いなぁ）。

D列

ここで線形合同法を実施します。結果は同じく0～65536の整数です。

=mod(75*C2 + 74, 65537)

線形合同法は次の式で数を変換していく方法です。

条件を満たすA、B、Mのパラメータを用いることで、乱数の周期を最大Mにすることができます。通常は M=2³² といった大きな数を用いますが、そんなに長い周期はいらないのでもっと簡単なパラメータがないか探してみます。以下の参考文献によると A=75, B=74, M=2¹⁶+1 で良いとのこと。

Linear congruential generator - Wikipedia

en.wikipedia.org

これで周期は65537になるのですが、今回の実装は数列ではなく単発の変換を繰り返しているだけなので線形合同法に起因する周期はないと思います。（他に起因する周期はあるかも）

プロットを見るとバラバラに見えます。

E列

最後にこれを65537で割って [0, 1) の小数にします。これで一様乱数っぽいものが完成しました。

=D2/65537

0.1刻みでカウントしてみるとだいたい100個ずつになりました。シードを10種類で変えたGIFを置いておきます。

抽選

あとは好きに抽選してください。当選確率50%ならこんな感じです。

=if(E2<0.5, 1, 0)

さいごに

これらを1列に押し込んだのがこちらです。

=mod(75*rounddown(32768.5*sin(申し込みID+32768*シード値)+32768.5,0)+74,65537)/65537

少し心配なのは、sin関数で-1付近の密度が高くなることに起因した乱数の偏りがありそうなことです。せいぜい100人程度の抽選なので許してもらうことにしましょう。