やること
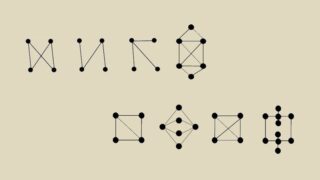
グラフと一筆書きの後編です。前回はいろいろなグラフがオイラーグラフ、準オイラーグラフ、ハミルトングラフに該当するか確認しました。
今回は数理的な判定方法を紹介し、魔法陣グルグルに出てくる「トーラ」や「トカゲのシッポ」の魔法陣を判定してみます。
私の身内だけかもしれませんが魔法陣グルグルの認知度は高い気がします。しかし、古い漫画なので詳しく知っている人はほとんどいません。布教のためにPVを貼ってきおきます。
参考文献
魔法陣グルグルの魔法陣一覧です
オイラーグラフについて

オイラーグラフとハミルトングラフについて
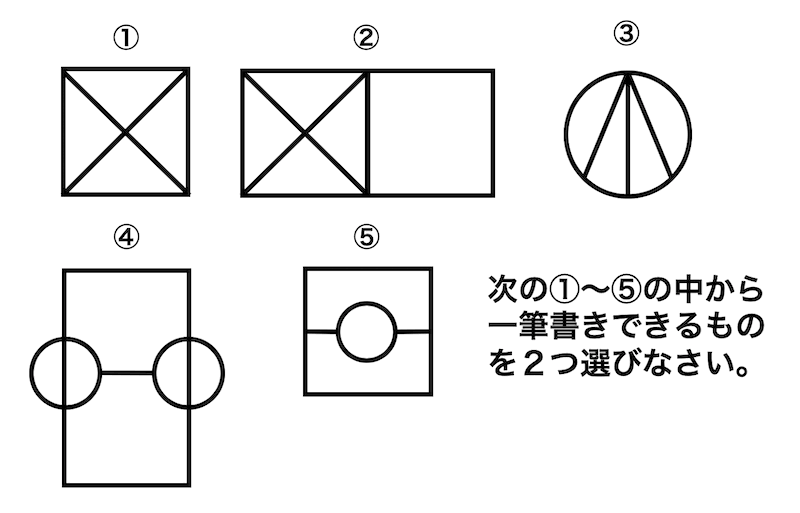
ハミルトン閉路について
https://school.gifu-net.ed.jp/ena-hs/ssh/H29ssh/sc3/31701.pdf
オイラーグラフと準オイラーグラフの判定方法
調べたところ、全ての頂点が偶点であることがオイラーグラフの条件(必要十分条件)のようです。
また、奇点がある場合は、奇点がちょうど2個であれば準オイラーグラフになるようです。(その2点が始点と終点になる)
それ以外の場合はオイラーでも準オイラーでもありません。
ハミルトングラフの判定方法
ディラック(Dirac)の定理
3個以上の点があるグラフで使える定理です。nを頂点数として、全ての頂点の次数 d(i) が n/2 以上であればハミルトングラフである、という定理です。
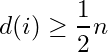
言い換えると、グラフの最小次数を d(i)min としたときに、
![]()
このように d(i)min を2倍した数がn以上であればハミルトングラフというわけです。
オーレ(Ore)の定理
隣接していない頂点が存在するグラフで使える定理です。すべての隣接しない2点の組み合わせにおいて、2点の次数の合計が頂点数以上であればハミルトングラフなのだそうです。
![]()
こちらも言い換えると、隣接しない2点の次数の合計、の最小値を {d(i) + d(j)}min としたときに、
![]()
これがn以上であればハミルトングラフというわけです。
どちらの定理も、関係する次数を全て確認しないといけないのでちょっと大変ですね。
魔法陣をチェックしてみる
オイラーグラフ、準オイラーグラフ、ハミルトングラフの判定方法を学んだので、前回の記事で登場したグラフを復習してみてください。
それでは、魔法陣グルグルの魔法陣をいくつか確認してみます。
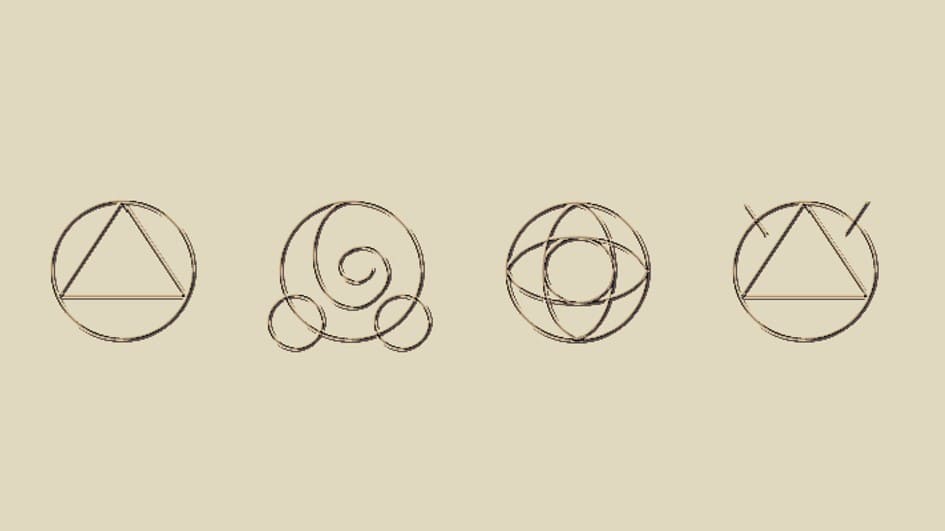
魔法陣:トーラ
まずはトーラです。最初に出てくる火の魔法です。火が垂直に出ます。

トーラを使うシーンです。懐かしいですね。

検証してみましょう。
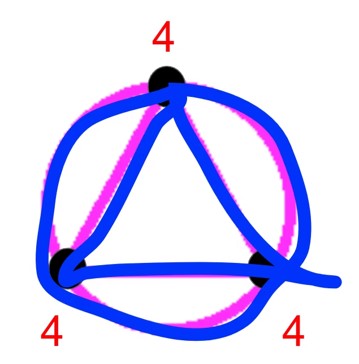
- 偶点:3個
- 奇点:0個
よってオイラーグラフであり、一筆書きできます。
頂点が3個以上あるのでディラックの定理が使え、最小次数は4ということで「2×4≧3」が成立してハミルトングラフでもあることが分かります。一方、全ての頂点が隣接するのでオーレの定理は使えません。
魔法陣:トカゲのシッポ
続いてトカゲのシッポです。トーラの円上に二つの直線を入れたものです。

これもトーラと同じ火の呪文でククリが使います。私が魔法陣グルグルを漫画で読んだときに一番印象に残った呪文です。トカゲのシッポーーーーーーーー!!!(※深夜2時です)
これも検証してみます。
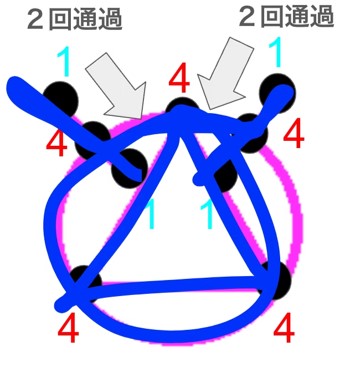
- 偶点:5個
- 奇点:4個
よって一筆書きできません。奇点が2個であれば準オイラーグラフになりますが、それも当てはまりません。
ディラックの定理を確認すると、最小次数は1で、「2×1≧9」は成立しないのでハミルトングラフではありません。
今回はオーレの定理が使えます。次数1の点を2個選べばいいですね(隣接していないので)。「2≧9」が成立せず、やはりハミルトングラフではありません。
魔法陣:ベームベーム召喚
こちら興味があれば自分で確かめてみてください。書き方によって線が接するか微妙なのですが、頂点数12として考えてください。

魔法陣:夢の回転木馬
こちらも良い練習問題になると思います。頂点数6として考えてください。
まとめ
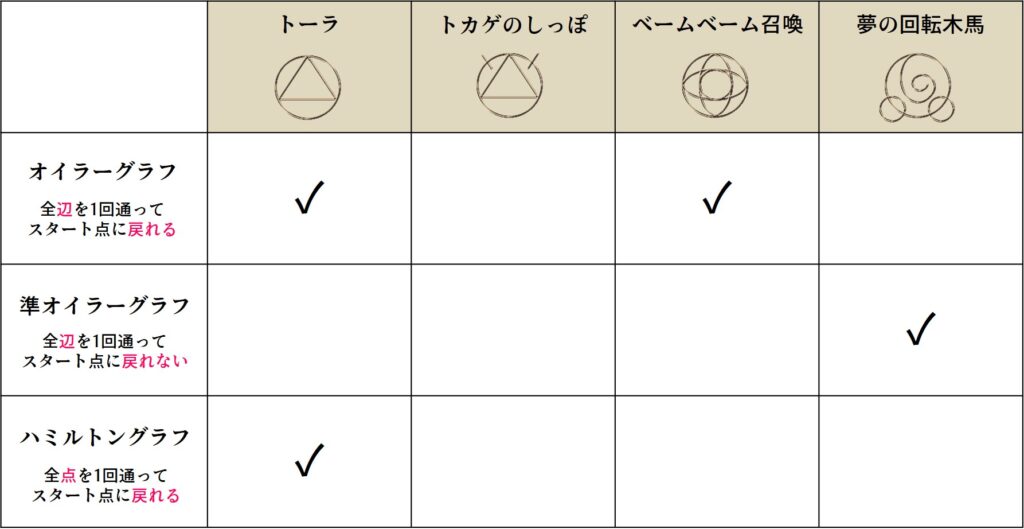
今回取り上げた魔法陣をまとめました。
さいごに
トーラはオイラーグラフ&ハミルトングラフでしたが、トカゲのシッポはどちらにも該当しませんでした。トカゲのシッポのように枝が3本以上生えているとダメですね。
時間があれば他の魔法陣も検証していきたいと思います。また、プログラムでの自動判定もやってみたいと思います。
応援はリツイートなどを実行する形でお願いします!また、Qiitaとnoteもやっていますのでフォローお願いします!
Qiita

note