やること
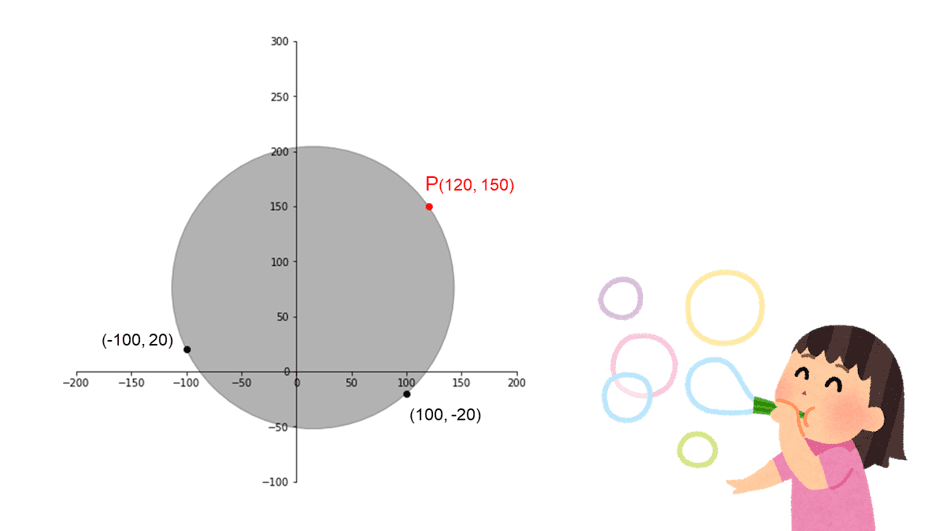
問題
次の3点を通る円を求めよ。(-100, 20), (100, -20), (120, 150)
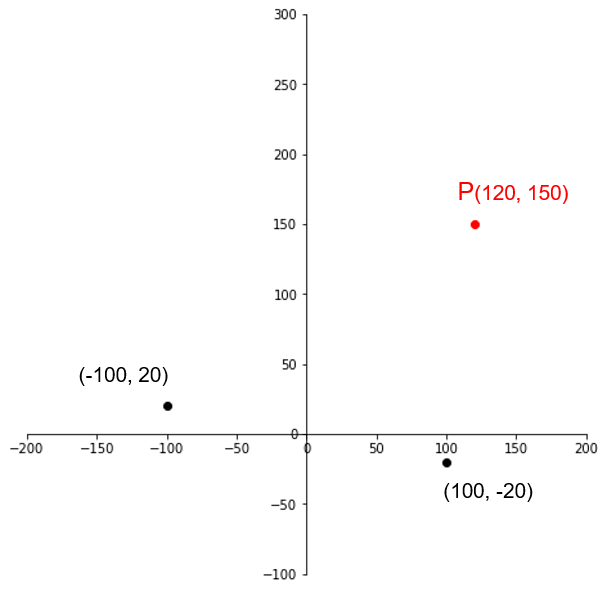
紙とペンを出すのが面倒なので、Pythonを使って解いてみましょう。
参考文献
Sympyという数式処理用のライブラリを用います。中学校や高校で習ったような連立方程式や微分積分を一瞬で解いてくれます。使い方はこちらによくまとまっています。

Python, SymPyの使い方(因数分解、方程式、微分積分など) | note.nkmk.me
SymPyは代数計算(数式処理)を行うPythonのライブラリ。 因数分解したり、方程式(連立方程式)を解いたり、微分積分を計算したりすることができる。 公式サイト: SymPy ここでは、SymPy...
実行環境
WinPython3.6をおすすめしています。
WinPython - Browse /WinPython_3.6/3.6.7.0 at SourceForge.net
Portable Scientific Python 2/3 32/64bit Distribution for Windows
Google Colaboratoryが利用可能です。

Google Colab
コードと解説
中心が (s, t), 半径が r である円の方程式は次の通りです。
![]()
3点の情報を x, y に代入すると3つの式ができますから、3つの未知数 s, t, r を求めることができそうです。
importと3点の定義です。
import matplotlib.pyplot as plt
import matplotlib.patches as pat
import sympy
#赤点(動かす点)
x = 120
y = 150
#黒点(固定する2点)
x_fix = [-100, 100]
y_fix = [20, -20]グラフを描画する関数を作ります。
#表示関数
def show(center, r):
plt.figure()
ax = plt.axes()
#動かす点の描画
ax.plot(x, y, 'or')
#固定点の描画
ax.plot(x_fix, y_fix, 'ok')
#円の描画
e = pat.Circle(xy=center, radius=r, color='k', alpha=0.3)
ax.add_patch(e)
#軸の設定
ax.set_aspect('equal')
ax.set_xlim(-200, 200)
ax.set_ylim(-100, 300)
ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('data', 0))
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
plt.show()
#確認
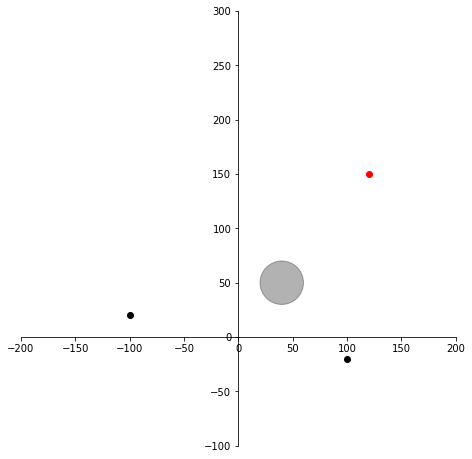
show((40, 50), 20)試しに中心(40, 50)、半径20の円を表示してみました。
Sympyを使って未知数 s, t, r を求めます。
#3点を通る円の方程式を求める
"""
中心(s, t), 半径rの円の方程式は
(x - s)**2 + (y - t)**2 = r**2
3点を通るという情報から未知数(s, t, r)を求める
"""
s, t, r = sympy.symbols('s t r') #変数を定義
eq1 = (x_fix[0] - s)**2 + (y_fix[0] - t)**2 - r**2 #1つ目の固定点を代入した式(=0の形)
eq2 = (x_fix[1] - s)**2 + (y_fix[1] - t)**2 - r**2 #2つ目の固定点を代入した式
eq3 = (x - s)**2 + (y - t)**2 - r**2 #動く点Pを代入した式
#方程式を解く
ans = sympy.solve([eq1, eq2, eq3], [s, t, r])
print('ans:{}'.format(ans))
s, t, r = ans[0]
print('s, t, r = {}, {}, {}'.format(s, t, r))
#表示
show((s, t), r)ans:[(1325/87, 6625/87, -5*sqrt(4974554)/87), (1325/87, 6625/87, 5*sqrt(4974554)/87)]
s, t, r = 1325/87, 6625/87, -5*sqrt(4974554)/87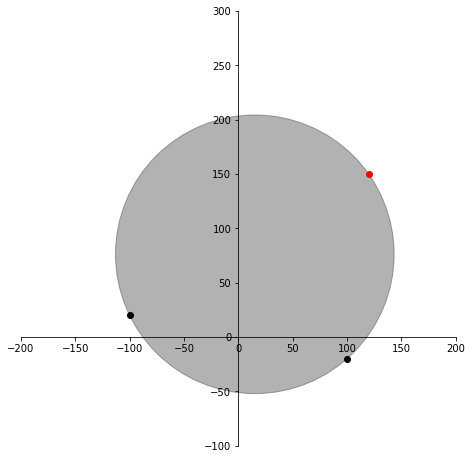
解が2セット出てきました。r の正負があるようですが、どちらでも描画に問題はありませんので0番目の解を採用しています。
点Pを動かしてみた
最後に、点Pを動かすアニメーションを作ってみました。